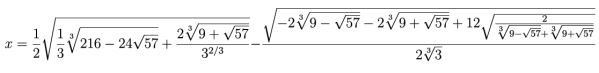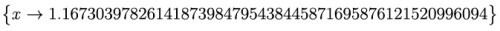Niels Henrik Abel i jego nagroda

Tyle suchej informacji. Po kolei o wszystkim. Zacznę od nagród za rozwiązywanie zadań. W czasach studenckich chodziłem na seminarium Stanisława Mazura, jednego z najwybitniejszych matematyków polskich lat trzydziestych. Opowiadał, że wraz z kolegami dawali sobie zadania matematyczne, nagrodą za rozwiązanie była butelka wina. „I wiecie państwo, na początku dawaliśmy sobie nawet trudne zadania, ale potem coraz łatwiejsze”. Ten sam Stanisław Mazur wyznaczył w 1936 roku za rozwiązanie już naprawdę trudnego problemu… żywą gęś. Problem rozwiązał 30-letni Szwed, Per Henrik Enflo, w 1972 roku. Przyjechał do Warszawy, gęś odebrał. Szkoda, że gęś nie doczekała kameralnej uroczystości następnego dnia wieczorem.

I jeszcze jedno wspomnienie. Profesor Andrzej Białynicki-Birula (1935–2021), od którego wiele się nauczyłem, też nagradzał nas za rozwiązania trudnych zadań, z tym że  nagrody były skromniejsze: jeden orzech laskowy, za trudniejsze zadanie jeden orzech włoski – a kiedyś zdarzyła się tabliczka czekolady. Nie pamiętam, czy ktoś ją zdobył.

Ale do rzeczy, czyli do matematyki. Niewielu Czytelnikom powie coś nazwisko Abel. Nie, nie chodzi o nieszczęśliwego młodzieńca, stanowiącego wtedy jedną czwartą ludzkości, zabitego przez własnego brata, Kaina. Mam na myśli matematyka norweskiego, Nielsa Henrika Abela (1802–1829) i nagrodę jego imienia. Wręczenie odbywa się ze stosowną pompą, w obecności króla. Nagroda ta rekompensuje matematykom pominięcie ich przez Alfreda Nobla w tej najważniejszej światowej nagrodzie naukowej. Co prawda matematycy bardziej cenią tak zwany medal Fieldsa, to jednak z medalem tym wiąże się tylko 15 tysięcy (nie milionów, tysięcy!) dolarów kanadyjskich, podczas gdy zdobywcy Nagrody Abela wsuwa się do kieszeni czek na 7,5 miliona koron norweskich (około 650 000 euro). Nobliści dostają 8 milionów SEK, czyli jakieś 865 tysięcy euro, mniej niż tenisiści za wygranie dużego turnieju. Jest kilka prawdopodobnych powodów, dla których Alfred Nobel nie uwzględnił matematyków jako ewentualnych biorców nagrody. Najprawdopodobniej Nobel nie zaliczył matematyki do pól działalności ludzkiej, przynoszących społeczeństwom największe korzyści. Może zresztą nie bez podstawy – korzyści, jakie mamy z odkryć matematycznych, ujawniają się na ogół po bardzo wielu latach i wtedy rozmywa się, kto jest naprawdę sprawcą. Jak wymierzyć twórcze rozwinięcie?

Kim był Niels Henrik Abel i czym się wsławił? Choć genialny, zmarł na gruźlicę w wieku zaledwie 27 lat. Z czego zdążył zaistnieć na stałe w matematyce? No cóż, każdy matematyk wie, czym jest grupa abelowa i co to są całki Abela. Ale nie o tym – omówię coś prostszego.

Otóż w szkole uczymy się rozwiązywać równania; najpierw pierwszego stopnia, potem kwadratowe i niekiedy sześcienne. Sześcienne – czyli trzeciego stopnia. Po trzecim stopniu idzie czwarty. Już 400 lat temu uczeni włoscy dawali sobie radę z takim równaniem, choćby i wyglądającym tak niewinnie

x⁴ + 4x + 2 = 0

a którego jednym z pierwiastków jest 

Tak, to umieli uczeni już w XVI wieku. Nietrudno zgadnąć, że wzięto się za równania wyższych stopni. I… nic. Przez dwieście lat nikomu się nie udawało. Nie udało się również Nielsowi Abelowi. I wtedy zrozumiał on, że… może w ogóle się nie da? Że można udowodnić, że się nie da! Ściślej: nie da się zapisać rozwiązania tego równania w prosty sposób, to znaczy za pomocą czterech podstawowych działań arytmetycznych i wyciągania pierwiastka. I tak właśnie jest. To było pierwsze od 2000 lat (!) rozumowanie tego typu: coś się nie da udowodnić, czegoś się nie da zrobić. Na takie dowody monopol ma matematyka – nauki praktyczne coraz to łamią kolejne bariery. W 1888 roku przewodniczący Komisji Patentowej USA oświadczył, że „niewielu wynalazków należy się spodziewać w przyszłości, ponieważ prawie wszystko zostało już wynalezione” („everything has been invented”). Dziś trudno się nam nawet z tego śmiać… A w matematyce – raz dowiedzione, przepadło. Nie da się i już.

Muszę tu  wyjaśnić istotną sprawę. Nie jest tak, że równania stopnia piątego nie da się rozwiązać. Da się – metod jest wiele. Chodzi o to, że liczba, która jest pierwiastkiem, choćby i takiego równania:

x⁵ - x - 1 = 0

nie da się zapisać za pomocą czterech podstawowych działań arytmetycznych i wyciągania pierwiastka (dowolnego stopnia). Wielomian 

ƒ(x) = x⁵ - x - 1

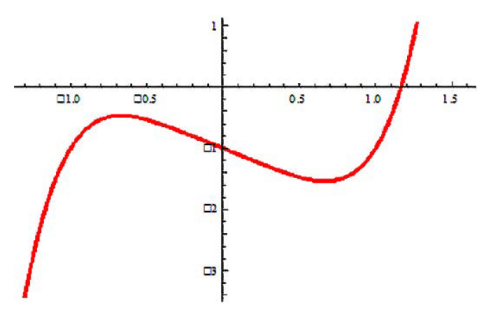
ma ładny wykres, miejsce zerowe to punkty, w których wykres przecina oś x. Mogę sobie obliczyć to z dowolną dokładnością, np.

Funkcja ƒ(x) = x⁵ - x - 1
ale nie znajdę wzoru, choćby dziesięć razy bardziej skomplikowanego niż ten widoczny powyżej dla równania czwartego stopnia. „Nie znajdę” go, nie ma. Abel udowodnił, że nie ma.

Autopoprawka. W historii nauki zdarza się, że ktoś coś odkrył – a potem okazuje się, że ktoś to odkrył wcześniej, tylko nie zostało to zauważone, a może nie było tak dobrze opracowane i nagłośnione. Dziś uważamy, że odkrycie, o którym wspominam, można też przypisać włoskiemu… lekarzowi (i uczonemu Paolo Ruffiniemu), a także i Ewarystowi Galois, zabitemu w pojedynku 21-latkowi, który spisał swoje odkrycia w noc przed tym fatalnym dla siebie dniem. W czasach mojej młodości popularna była książka wybitnego fizyka polskiego, współpracownika Alberta Einsteina, Ewaryście Galois: „Wybrańcy bogów”.

Abel i Galois, jako „wybrańcy bogów”, zmarli przed trzydziestką, niedoceniani przez współczesnych. Niels Abel jest jednym z niewielu) matematyków norweskich o szerokiej sławie (właściwie dwóch, drugi to Sophus Lie, 1842–1899). Nazwiska nie brzmią skandynawsko, ale obydwaj byli rdzennymi Norwegami.

Norwegowie są skłóceni ze Szwedami. To się zdarza wśród sąsiadujących narodów. Jednym z motywów ustanowienia Nagrody imienia Abela przez Norwegów była właśnie chęć pokazania rodakom Alfreda Nobla: o proszę, my nie gorsi.

Tyle o Nielsie Henriku Abelu. Teraz o tym, co robił Michel Tallagrad. Nie da się tego w prosty sposób opisać, ale spróbuję. Jest to probalistyka, czyli rachunek prawdopodobieństwa – i procesy stochastyczne, czyli właśnie zjawiska, w których dużą rolę gra przypadek. Podam przykład takiego procesu, z własnych doświadczeń turystycznych. Niedaleko Warszawy jest Puszcza Kampinoska. W niej drogi i ścieżki, jak to w lesie. Bawiłem się kiedyś tak. Wyruszałem na spacer, dochodziłem do rozwidlenia i rzucałem monetę. Orzeł = idę w lewo. Reszka = idę w prawo. Uff, bywało, że kręciłem się wokół jednego zagajnika. Ale to jest dobry przykład procesu stochastycznego.

Teraz o samym prawdopodobieństwie. Dla niektórych Czytelników to była (będzie?) zmora na lekcjach matematyki. Nie dziwię się. To trudny kawałek. Niewiele jest pojęć matematycznych tak fałszywie pojmowanych i tak źle uczonych w szkole jak prawdopodobieństwo. O przyczynach tego dyskutują dydaktycy. Ja tylko wspomnę, że jeszcze 100 lat temu rachunek prawdopodobieństwa nie był zaliczany do matematyki – lecz do fizyki.

Zastanówmy się nad rachunkiem szans, tak ważnym dla banków, towarzystw ubezpieczeniowych i firm prowadzących gry liczbowe, jak ważny jest rachunek całkowy dla inżyniera. Chociaż probabilistyka była stosowana od 200 lat z okładem, uzyskała solidne matematyczne podstawy dopiero w latach trzydziestych XX wieku. W rachunku prawdopodobieństwa często używamy bowiem tak niejasnych i nieostrych terminów jak prawie na pewno czy około i jeżeli chcemy zaliczyć go do matematyki, musimy nawet i takim pojęciom nadać precyzyjne i jednoznaczne (czyli matematyczne) znaczenie. Może właśnie dlatego matematyczne podstawy teorii prawdopodobieństwa są trudne.

Co to jest przypadek? Co to jest szansa? Jak bardzo prawdopodobne jest jakieś zdarzenie? Takie pytania mogą przychodzić do głowy codziennie, ale na ogół nie zaprzątamy nimi sobie zanadto głowy, bo każdy intuicyjnie wyczuwa, o co chodzi.

O tym, która drużyna zaczyna mecz piłkarski, decyduje los. Rzucona przez sędziego moneta może upaść na reszkę albo na orła. Wynik rzutu wskazuje, komu przypadnie piłka – a raczej, kto wybiera „boisko czy piłka”. To jest sprawiedliwe losowanie, bo moneta „równie często” pada reszką, jak i orłem do góry.

Co to jednak znaczy „równie często”? Jeżeli na sto rzutów monetą, otrzymamy 51 reszek i 49 orłów, nie uznamy tego za coś podejrzanego. „Mieści się w granicach normy” – powiemy. Ale odchylenie 70:30 uznamy już – słusznie –  za niezwykłe, choć niesłychanie rzadko może się to zdarzyć i przy uczciwym rzucaniu. Odwrotnie, jeżeli przy dziesięciu tysiącach rzutów wypadłoby 5000 reszek i 5000 orłów, podejrzewalibyśmy, że taka precyzja jest wynikiem jakiejś manipulacji. Może ktoś pamięta, ze kilkanaście lat temu w grze losowej w Bułgarii w dwóch kolejnych tygodniach wylosowano dokładnie te same liczby?

Nie potrzeba się uczyć matematyki, żeby wiedzieć, że prawdopodobieństwo wyrzucenia orła przy rzucie monetą jest równe 1/2, czyli 50%, fifty-fifty. Kostka do gry może pokazać jedną z liczb od 1 do 6 i mamy jednakowe szanse na każdą z nich. Losowo wyciągnięta karta z talii do brydża może być asem – z prawdopodobieństwem 1/13, a to dlatego, że wszystkich kart jest 52, wśród nich 4 asy, no a 52:4=13. Możemy się spodziewać, że jeżeli automat będzie tasował karty i wyciągał losowo jedną, zapisywał, jaka ona jest, wkładał z powrotem do talii, tasował, wyciągał następną i tak dalej, to po bardzo długiej serii takich doświadczeń „prawie na pewno” około 1/13 to będą asy. Ujmuje to ściśle prawo wiel-kich liczb, które możemy sformułować mniej więcej tak: rzeczywisty rozkład wyników serii doświadczeń losowych jest tym bliższy idealnemu, teoretycznemu, im dłuższa jest seria. Dlatego właściciele sieci kasyn, Totolotka i wszelkich innych gier losowych mogą spać spokojnie. Matematyka zapewnia im stały przypływ gotówki. Bywają gorsze dni: ktoś gdzieś trafi w numer, wybierze wygrywającą szóstkę liczb, może nawet rozbije bank w jakimś małym kasynie i nie znaczy to, że następnego dnia wszystkim będzie źle iść, żeby się straty wyrównały, tylko że... jakoś to będzie. Prędzej czy później dobra passa grających się skończy... prawie na pewno: z taką samą pewnością, jak to, że nie zginiemy jutro od upadku meteorytu. Prawo wielkich liczb należy do matematyki, tak jak i twierdzenie Pitagorasa.

Jeżeli rzucamy monetą 10 razy, to prawdopodobieństwo, że liczba orłów będzie 4, 5 lub 6, jest w przybliżeniu równe 0,66. Dla 100 rzutów prawdopodobieństwo, że otrzymamy nie mniej niż 40, a nie więcej niż 60 rzutów, jest już równe około 0,9648, a gdybyśmy rzucili tysiąc razy i wypadło mniej niż 400 000 albo więcej niż 600 000 orłów, bylibyśmy świadkami zjawiska, którego teoretyczne szanse są poniżej jednego do miliarda. Im więcej prób, tym dokładniejszy jest rachunek wyjaśnia właśnie prawo wielkich liczb.

Rachunek prawdopodobieństwa wyjaśnia też, kiedy mamy prawo podejrzewać – ale tylko podejrzewać – że coś jest nie tak, że tych zbiegów okoliczności jest za dużo. Szansa, że na 10000 rzutów moneta padnie na reszkę dokładnie 5000 razy, wynosi tylko osiem promil, czyli 1 do 125, a że na 100 rzutów liczba reszek będzie mniejsza niż trzydzieści, jest równa około 0,000016, szesnaście do miliona. Rzucanie monetą bardzo dobrze ilustruje nieubłagalność prawa wielkich liczb: choć nie sposób przewidzieć wyniku pojedynczego rzutu, to nie ma ucieczki od żelaznych reguł rządzących prawdopodobieństwem.

Witold Bednorz i Rafał Latała zajęli się teorią schematu Bernoullego. W bardzo uproszczonej wersji spotykamy się z tym w szkole średniej. Znów rzucamy monetą, ale wiele razy. Za każdym rzutem: albo orzeł, albo reszka. Zero albo jeden. Plus albo minus. Jaki będzie „ostateczny wynik”. To znaczy, jakie jest prawdopodobieństwo, że na 100 rzutów będzie tyle a tyle orłów? To jest materiał ostatniej klasy szkoły średniej – nietrudny. Maturzyści 2025: pamiętajcie o schemacie Bernoullego.

Znacznie trudniej jest, gdy mamy nie tylko binarną, zerojedynkową sytuację. Czy da się nad tym zapanować? Otóż Bednorz i Latała pokazali, że się da. Zastosowania takiej matematyki w analizie finansowej były znane już wcześniej. Odkrycie polskich matematyków ulepsza te narzędzia finansistów.

Można to zrozumieć na przykładzie VaR. Nie, nie jest to znany ze sportu VAR (video assistant referee, wideorejestracja), tylko Value at Risk – ryzyko inwestycyjne. Wyobraźmy sobie, że zastanawiamy się, w co zainwestować nasz ciężko (albo i lekko, czego wszystkim życzę) zarobiony milion złotych, dolarów czy euro. Mamy wiele możliwości. Każda daje pewien zysk, ale obarczona jest pewnym ryzykiem. W przypadku plajty możemy nawet nie tylko stracić włożone pieniądze, ale stracić jeszcze więcej – na przykład, gdy użyczymy własnych maszyn, które zostaną zniszczone, albo stracimy rozczarowanych niepowodzeniem dobrych fachowców, albo – co oczywiście najgorsze – reputację. Wszystko jest płynne, zmienne, niepewne. Jakie pytania sobie stawiamy? Główne pytanie to oczywiście: jak skonstruować „portfel”, żeby zmaksymalizować zysk z maksymalnym prawdopodobieństwem? Ale samo to pytanie ma dwie strony: czy bardziej zależy nam na bezpieczeństwie, czy na wielkości zysku. Gdy drużyna piłki ręcznej albo hokeja przegrywa na minutę przed końcem jedną bramką, to wycofuje bramkarza, przedkładając ryzyko nad bezpieczeństwo. Ale kolarz w wyścigu przełajowym, jadący z dużą przewagą na ostatniej rundzie, skupi się na bezpieczeństwie. To jasne i zrozumiale.

Możemy stawiać wiele innych pytań. Może pamiętacie, drodzy Czytelnicy, skecz „Sęk”? W nim Beniek Rappaport (Edward Dziewoński) namawia Kubę Goldberga (Wiesław Michnikowski) do pewnej operacji finansowej. Obudzony w nocy Kuba od  razu zadaje sensowne pytanie: „ile można stracić?”. Na zachętę Beńka („ty pytaj, ile można zarobić?”) odpowiada rzeczowo, ze stosownym akcentem: „ile trzeba mieć w razie się straci?”.

I to jest następne pytanie: oszacować, z jakim prawdopodobieństwem stracimy tyle a tyle. I wreszcie pytanie niemal metafizyczne: ile warte są te wszystkie wyliczenia? Czyli: obliczyć prawdopodobieństwo, że prawdopodobieństwo wynosi tyle a tyle.

***

W świecie naukowym o randze odkrycia najczęściej decyduje ranga czasopisma, w którym praca zostaje opublikowana. Działa tu oczywiście sprzężenie zwrotne: najlepsze czasopisma są dlatego najlepsze, że wysyłają tam prace najlepsi uczeni – na lokalną skalę jest przecież podobnie i z reputacją szkół. Tak czy owak „Annals of Matematics”, (tom 180, rok 2014), gdzie została opublikowana praca Bednorza i Latały, to jedno z najlepszych czasopism.

Na zakończenie jeszcze jedna ważna uwaga. Bednorz i Latała nie dali odpowiedzi na te pytania. Pewnie byliby zdziwieni, że w ten sposób opisuję ich odkrycie. Zajmowali się tylko matematyką, która między innymi może odpowiedzieć i na takie pytania. 

Michał Szurek