Narzędzia matematyczne dla ucznia: GeoGebra (2)
Okrąg w różnych sytuacjach
Będzie to zatem najpierw okrąg o środku w danym punkcie, przechodzący przez jakiś inny dany punkt. Najpierw więc rysuję tak, jak to było opisane poprzednio, punkty A i B, następnie po kliknięciu szóstej ikony od lewej w pasku narzędziowym klikam najpierw A (to będzie środek), potem B. Okrąg powstały na bazie tych dwóch punktów jest obiektem zależnym.
Przy okazji: skorzystałem z możliwości zapisania konstrukcji jako rysunku, bez menu, ramek itp. Robi się to korzystając z menu Plik i wybierając opcję eksportu do pliku; wybrałem uniwersalny format graficzny png z kilku dostępnych. Dalsze rysunki są po prostu zrzutami odpowiednich ekranów, ponieważ chciałem, by widoczne były ikony i opcje programu.
Z kolei skonstruujemy okrąg, mając dane trzy kąty, przez które on przechodzi. Jest to oczywiście możliwe, ponieważ na każdym trójkącie da się jednoznacznie opisać okrąg; innymi słowy, trzy dane nie współliniowe punkty wyznaczają tę krzywą jednoznacznie.
Niech to będą zatem punkty A, B, C. Rysujemy te punkty, następnie klikamy na małym trójkąciku na szóstej od lewej ikonie, wybieramy odpowiednie narzędzie z menu, które się rozwinie ? i mamy:
Rozwijając to samo narzędzie narysujemy wycinek koła, mając dany jego środek A i dwa punkty na obwodzie, B i C:
Stożkowe
Następne narzędzie GeoGebry ? siódma ikona od lewej ? służy do kreślenia stożkowych. Przypomnę (kto nie wie), że stożkowymi (inaczej: konikami, od conus-stożek naturalnie, nie od konika!) nazywamy krzywe, które można uzyskać w różny sposób tnąc nieskończoną powierzchnię stożkową; na ogół używając tego terminu mamy na myśli elipsę (jej szczególnym przypadek jest okrąg), hiperbolę i parabolę.
Rozwijając menu, możemy tu narysować elipsę (mając dwa punkty A i B jako ogniska i punkt C na brzegu):
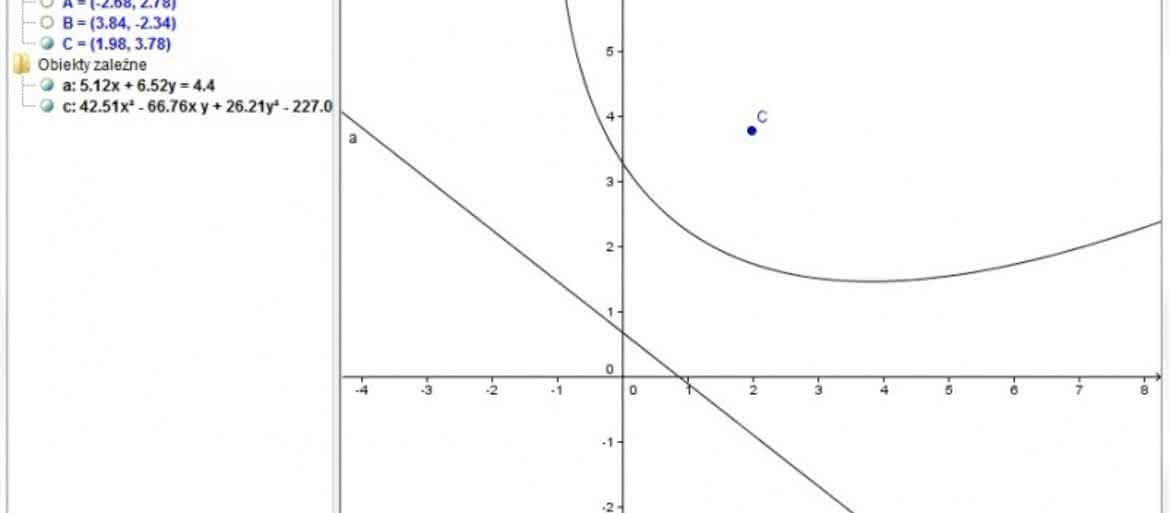
Możemy narysować na podobnej zasadzie (dwa ogniska i punkt na krzywej) hiperbolę:
I wreszcie, mając daną prostą (kierownicę) i punkt (ognisko) zbudujemy parabolę (jest to zbiór punktów płaszczyzny, jednakowo oddalonych od danej prostej, zwanej kierownicą właśnie, i ustalonego punktu, zwanego ogniskiem):
Na koniec ? zilustrujemy znane twierdzenie o pięciu punktach, wyznaczających jednoznacznie przechodzącą przez nie stożkową (gdy mamy dane pięć punktów, z których żadne trzy nie są współliniowe, to wyznaczają one jednoznacznie pewną przechodząca przez nie stożkową):
Jak widać, wybrana przez mnie piątka wyznaczyła akurat elipsę. Spróbujcie dobrać wyjściowe punkty tak, by otrzymać parabolę lub hiperbolę (wskazówka: problem należy rozwiązać ?od tyłu? ? wykreślić na początku planowaną krzywą, a potem dobrać na niej odpowiednio pięć punktów).
















