Narzędzia matematyczne dla ucznia: GeoGebra (5)

Powiedzmy, że interesuje nas zachowanie dwóch funkcji:

f(x) = sin (nx)

oraz

g(x)=x^(1/n)

dla n zmieniającego się od -5 do 5.

Postępujemy następująco.

Po otwarciu programu w pole edycyjne u dołu wpisujemy najpierw formułę n=1. W części algebraicznej pojawi się oczywiście ten zapis, będzie przy nim z lewej strony widoczne małe białe kółeczko.

Teraz po kolei wpisujemy wyrażenia, definiujące obie funkcje. Pamiętajmy, ze piszemy je w formie y= coś tam; nazwy funkcji (f, g i kolejne ? jeśli trzeba) wybierze program samodzielnie i automatycznie.

Dalej ? klikamy na wspomnianym wyżej kółeczku przy definicji zmiennej n. W tym momencie na ekranie pojawia się odcinek z zaznaczonym punktem, i przypisaną mu wartością 1. Ten odcinek ? to tzw. suwak. Chwytając zaznaczony na nim punkt i przesuwając go w lewo lub w prawo ? zmieniamy wartość n w domyślnym przedziale od -5 do 5; jednocześnie w części graficznej okna GeoGebry obserwujemy odpowiednie zmiany wykresów obydwu funkcji.

Proszę spojrzeć na rysunek; wartość n ustaliłem na -1 (ciekawy przypadek; dlaczego?):

[caption id="attachment_4993" align="aligncenter" width="300" caption="Animacja wykresów funkcji"][/caption]

Narzuca się pytanie: a co zrobić, jeśli chcemy wartość parametru zmieniać nie w przedziale

[- 5, 5], a w jakimś innym zakresie?

Nic prostszego. Klikamy na suwaku prawym klawiszem myszki i z rozwiniętego w ten sposób menu kontekstowego wybieramy opcję ostatnią, Właściwości. W otwartej automatycznie zakładce Suwak znajdujemy dwa pola na wpisanie pożądanej wartości początkowej i końcowej parametru. To wszystko. Przy okazji zauważmy, że w tej samej zakładce możemy zmienić orientację suwaka z domyślnie poziomej na pionową; możemy też zmienić jego długość z domyślnej wartości 100 na dowolną inną, wedle życzenia. Możemy tu również zmienić tzw. krok, czyli określić sposób zmiany parametru przy minimalnym przesunięciu. Na naszym rysunku n zmienia się co 0,1 ? oczywiście, moglibyśmy zażądać, by zmieniało się na przykład co 1.

Na marginesie: nie jest to jedyny (choć, moim zdaniem, naturalny i prosty) sposób wstawiania suwaka do wykresu. Zamiast klikać białe kółeczko przy zdefiniowanym parametrze można także kliknąć na pasku narzędziowym ikonę narzędzia Suwak. Ten sposób jest o tyle wart uwagi, że pozwala ona wybór miejsca wstawienia tego narzędzia na rysunku.

Aby nauczyć się obsługiwania suwaka dla parametrów kątowych rozważmy zadanie następujące: dane są dwa punkty na płaszczyźnie, A i B, oraz pewien kąt ?. Łączymy punkty A i B, następnie z punktu B prowadzimy półprostą pod kątem ? i odkładamy na niej odcinek równy odległości AB. Otrzymujemy w ten sposób punkt A?. Jak zmienia się położenie tego punktu zależnie od wartości kąta ??

W oknie graficznym GeoGebry ustalamy położenie punktów A i B. Następnie klikamy na pasku narzędziowym ikonę suwaka i wstawiamy suwak na rysunek. W oknie właściwości suwaka zmieniamy ?liczba? na ?kąt?. W pole edycyjne wpisujemy teraz formułę

Kąt[A,B,?]

(symbol kata znajdziemy na dolnym pasku narzędziowym GeoGebry, po prawej stronie) i dajemy Enter. W polu algebry pojawią się wyliczone współrzędne punktu A? oraz kąt o nazwie ?; to właśnie jest ten zależny kąt. Spójrzmy na rysunek:

[caption id="attachment_4994" align="aligncenter" width="300" caption="Kąt jako parametr"][/caption]

Oczywiście możemy nie tylko suwakiem zmieniać wartość kąta, ale także przesuwać myszką zaznaczone na początku pracy punkty. W ogóle pamiętajmy, że obiekty oznaczone w programie jako swobodne są? naprawdę swobodne, tzn. można je dowolnie zmieniać, przesuwać itp.

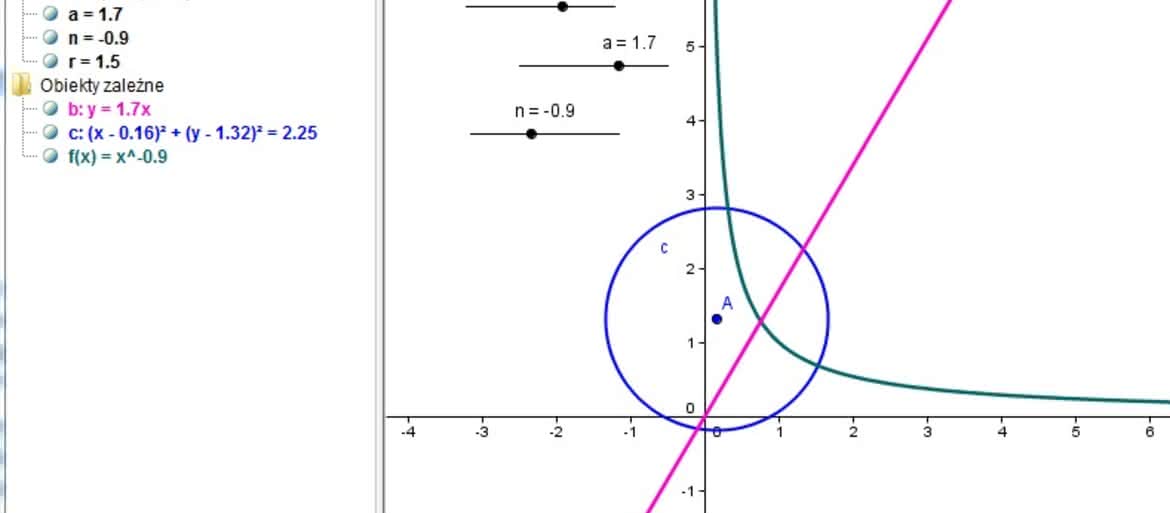
Żeby zakończyć sprawę suwaków: może ich być dowolnie wiele; tyle, ilu parametrów wpływ na konstrukcję chcemy badać. Oto przykład. Dany jest okrąg o promieniu r i środku w punkcie A, prosta o równaniu y=ax oraz krzywa y=x^n. Parametrami są r, a oraz n.

Oto stosowny rysunek:

[caption id="attachment_4995" align="aligncenter" width="300" caption="Kilka suwaków"][/caption]

Postępowałem tak:

Zacząłem od (dowolnego) wybrania punktu A. Następnie wprowadziłem trzy suwaki, wpisując jako nazwy zmienianego parametru odpowiednio r, a i n. Teraz kolejno wprowadziłem na rysunek okrąg o promieniu r (jest stosowne narzędzie na górnym pasku) oraz obie funkcje (poprzez okienko edycyjne, wpisując odpowiednie formuły). No teraz mogę dowolnie zmieniać parametry i obserwować co się będzie działo. Na przykład, badać różne punkty przecięcia wybranych obiektów; kto wie, może takie zajęcie nasunie mi sformułowanie jakiegoś ciekawego twierdzenia?

W ten sposób wraz z GeoGebrą wkracza do instrumentarium matematyka eksperyment.

Zostawimy teraz na chwilę funkcje graficzne GeoGebry i wrócimy do jej możliwości obliczeniowych. Są one zaskakująco duże; mówiliśmy już o obliczeniach numerycznych z użyciem funkcji, wspomnieliśmy o zastosowaniach statystycznych ? skupmy się teraz na chwilę na rachunku macierzowym.

Kto nie wie o co chodzi ? dwa słowa wyjaśnienia, rzecz jest dosyć prosta. Otóż macierzą nazywamy po prostu tablicę, utworzoną z liczb (czasami i z innych elementów, ale to już ?wyższa szkoła jazdy?). Te liczby w macierzy układają się w wiersze i kolumny; specjalnie ciekawy przypadek jest wtedy, gdy liczby kolumn i wierszy są jednakowe. Macierz nazywa się wówczas kwadratową.

Weźmy teraz pod uwagę dowolny układ n równań algebraicznych liniowych z n niewiadomymi. Jest rzeczą oczywistą, że współczynniki tych równań przy niewiadomych układają się w pewną tablicę, macierz właśnie ? i w dodatku w naszym wypadku kwadratową.

Dla takiej macierzy określa się pewną liczbę, zwaną wyznacznikiem. Mniejsza w tym momencie o definicję tej liczby; ważne jest to, że dany układ równań ma rozwiązania wtedy i tylko wtedy, kiedy ta liczba jest różna od zera. Obliczenie jej ?na piechotę? jest jednak dość żmudne i skomplikowane - tym bardziej, im większy układ równań bierzemy pod uwagę. Już dla układu czterech równań z czterema niewiadomymi obliczenie wyznacznika nie jest miłe.

Tymczasem GeoGebra robi takie rzeczy w mgnieniu oka.

W okno edycyjne wpiszmy taką oto formułę:

Wyznacznik[{{1, 2}, {3, -7}}]

Zauważmy konstrukcję: po nazwie operacji (Wyznacznik) następuje nawias kwadratowy, potem nawias klamrowy, w kolejnym nawiasie klamrowym liczby pierwszego wiersza przykładowej macierzy, w następnym ? drugiego wiersza, zamknięcie klamry, zamknięcie nawiasu prostokątnego ? i wszystko. W polu algebraicznym GeoGebry ukazał się zapis a=13. Program obliczył szukany wyznacznik i wybrał dla niego nazwę.

Ktoś mógłby się skrzywić, że przy stosunkowo prostej macierzy o wymiarach dwóch wierszy na tyleż kolumn było sporo pisania i jeszcze na dodatek trzeba było uważać na te wszystkie nawiasy. Faktycznie, w tym wypadku są reguły pozwalające odpowiednie obliczenia wykonać nawet w pamięci; ale zapewniamy Szanownych Czytelników, że już przy dziesięciu równaniach z dziesięcioma niewiadomymi znacznie łatwiej jest trochę skupić uwagę przy ? bezmyślnym w końcu ? pisaniu długiej formuły, niż łamać głowę nad skomplikowanymi obliczeniami, dla których w dodatku nie ma gotowych prostych wzorów?

Troszkę bardziej zaawansowanym matematycznie czytelnikom donoszę uprzejmie, że GeoGebra potrafi również odwracać i transponować macierze. Odpowiednie polecenia to Transpozycja i Odwrotność ? a po nich wypisuje się współczynniki macierzy dokładnie tak samo, jak w przykładzie cytowanym powyżej.

(korzystałem obficie ? za zezwoleniem Autora ? ze znakomitego podręcznika GeoGebry, opracowanego przez Pawła Wimmera, który znajduje się (podręcznik, nie Paweł) tutaj.)