Tworzenie muzyki. Mastering - część 2

Poprzedni artykuł zakończyłem pytaniem, jak to się dzieje, że w takim pofalowanym przebiegu (1) niejako zakodowana jest cała treść muzyczna, nawet jeśli chodzi o wiele instrumentów grających partie wielogłosowe? Oto odpowiedź: wynika to z faktu, że każdy dźwięk złożony, nawet o bardzo dużym stopniu tej złożoności, tak naprawdę składa się z wielu dźwięków prostych o przebiegu sinusoidalnym.
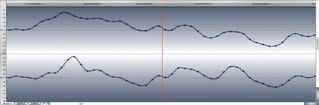
Sinusoidalność tych przebiegów prostych zmienia się zarówno w funkcji czasu jak i amplitudy, owe przebiegi nakładają się, dodają, odejmują, modulują się wzajemnie i w ten właśnie sposób powstają najpierw dźwięki poszczególnych instrumentów, a potem całe kompletne miksy i nagrania.
To, co widzimy na ilustracji 2, to swoiste atomy, cząsteczki, z których zbudowana jest nasza dźwiękowa materia, przy czym w przypadku sygnału analogowego takich atomów nie ma - jest jedna, płynna linia, bez punktów wyznaczających kolejne próbki (różnicę widać na ilustracji w postaci schodków, które są aproksymowane graficznie dla uzyskania odpowiedniego efektu wizualnego).
Ponieważ jednak odtwarzanie nagranej muzyki, czy to ze źródeł analogowych czy cyfrowych, musi się odbywać z wykorzystaniem przetwornika mechanicznego, elektromagnetycznego, jakim jest głośnik lub przetwornik w słuchawkach, więc w znaczącej większości przypadków różnica między dźwiękiem całkowicie analogowym a dźwiękiem przetwarzanym cyfrowo się zaciera. Na końcowym etapie, czyli podczas słuchania, muzyka i tak dociera do nas analogowo, jako drgania cząstek powietrza wywołane przez ruch membrany w przetworniku.
Analogowa cyfra
Czy istnieją słyszalne różnice między dźwiękiem całkowicie analogowym (czyli nagranym analogowo na analogowym magnetofonie, zmiksowanym na analogowej konsolecie, wytłoczonym na analogowej płycie, odtworzonym przez analogowy gramofon i wzmocnionym przez analogowy wzmacniacz) a dźwiękiem cyfrowym - przetworzonym z postaci analogowej do cyfrowej, obrabianym i miksowanym cyfrowo, a następnie przetworzonym znów do postaci analogowej, czy to tuż przed wzmacniaczem, czy też już praktycznie w samym głośniku?
W znaczącej większości przypadków raczej nie, choć gdybyśmy identyczny materiał muzyczny nagrali zarówno jedną, jak i drugą metodą, a następnie odtworzyli, to różnice na pewno byłyby słyszalne. Będzie to jednak wynikać bardziej z natury samych narzędzi wykorzystywanych w tych procesach, ich charakterystyk, właściwości, a często też ograniczeń, niż z samego faktu zastosowania technologii analogowej bądź cyfrowej.
W tym momencie przyjmijmy więc, że sprowadzenie dźwięku do postaci cyfrowej, czyli takiej właśnie wyraźnie zatomizowanej, nie ma istotnego wpływu na sam proces nagrywania i przetwarzania, tym bardziej, że próbki te występują z częstotliwością, która - przynajmniej teoretycznie - znajduje się daleko poza górną granicą częstotliwości przez nas słyszalnych, a zatem ta swoista ziarnistość dźwięku zamienionego na postać cyfrową jest przez nas niezauważalna. Z punktu widzenia masteringu materiału dźwiękowego ma ona jednak duże znaczenie, i będziemy jeszcze o tym mówić.
Teraz zajmijmy się tym, jak to się dzieje, że sygnał analogowy zostaje zamieniony na postać cyfrową, a dokładnie zero-jedynkową, czyli taką, gdzie napięcie może mieć tylko dwa poziomy: poziom cyfrowej jedynki, oznaczający istnienie napięcia, i poziom cyfrowego zera, czyli praktyczny brak tego napięcia. Wszystko w świecie cyfrowym jest jedynką albo zerem, nie ma wartości pośrednich. Oczywiście, w technologii istnieje też tzw. logika rozmyta, gdzie pomiędzy stanami "jest" lub "nie ma" funkcjonują jeszcze stany pośrednie, ale nie ma ona zastosowania w cyfrowych systemach szeroko pojętego audio.
Przemiany część pierwsza
Każdy sygnał akustyczny, czy to wokalny, czy pochodzący z gitary akustycznej albo perkusji, aby trafić do komputera w postaci cyfrowej, musi być najpierw zamieniony na postać zmiennego sygnału elektrycznego. Dokonuje się tego zazwyczaj za pomocą mikrofonów, w których drgania cząstek powietrza, wywoływane przez źródło dźwięku, wprawiają w ruch bardzo lekką strukturę membrany (3). Może to być membrana będąca elementem kapsuły pojemnościowej, wstęga z metalizowanej folii w mikrofonie wstęgowym lub membrana z przymocowaną do niej cewką w mikrofonie dynamicznym.
W każdym z tych przypadków, na wyjściu mikrofonu pojawia się bardzo słaby, zmienny sygnał elektryczny, który w mniejszym lub większym stopniu zachowuje proporcje częstotliwości i poziomu odpowiadające tym samym parametrom drgających cząstek powietrza. Jest więc swego rodzaju jego elektrycznym odpowiednikiem, który dalej może już być przetwarzany w urządzeniach przetwarzających zmienny sygnał elektryczny.
Na początku sygnał z mikrofonu musi zostać wzmocniony, gdyż jest zbyt słaby, by mógł być w jakikolwiek sposób wykorzystany. Typowe napięcie wyjściowe z mikrofonu ma poziom rzędu tysięcznych części wolta, czyli wyrażony jest w miliwoltach, a często w mikrowoltach, czyli milionowych częściach wolta. Dla porównania dodajmy, że zwykła bateria paluszkowa wytwarza napięcie 1,5 V, przy czym jest to napięcie stałe, niepodlegające modulacji, a tym samym nieprzenoszące żadnej informacji o charakterze dźwiękowym.
Napięcie stałe jest jednak potrzebne w każdym układzie elektronicznym po to, aby być źródłem energii, która następnie będzie modulowana sygnałem zmiennym. Im czystsza i bardziej wydajna jest ta energia, mniej podatna na obciążenia prądowe i zakłócenia, tym czystszy będzie sygnał zmienny przetwarzany przez elementy elektroniczne. Dlatego tak duże znaczenie w każdym układzie analogowym audio ma źródło zasilania, a konkretnie zasilacz.
Wzmocnieniem sygnału z mikrofonów zajmują się wzmacniacze mikrofonowe, zwane też przedwzmacniaczami lub preampami (4). Ich zadaniem jest wzmocnienie sygnału często nawet o kilkadziesiąt decybeli, co oznacza zwiększenie ich poziomu setki i więcej razy. W ten sposób na wyjściu przedwzmacniacza uzyskamy napięcie zmienne, wprost proporcjonalne do napięcia wejściowego, ale większe od niego setki razy, czyli na poziomie od ułamków do pojedynczych woltów. Taki poziom sygnału określa się poziomem liniowym i jest on standardowym poziomem roboczym w urządzeniach audio.
Przemiany część druga
Analogowy sygnał o takim poziomie może już zostać poddany procesowi przetwarzania na postać cyfrową. Dokonuje się tego za pomocą narzędzi zwanych przetwornikami lub konwerterami analogowo-cyfrowymi (5). Proces konwersji w klasycznym trybie PCM, czyli modulacji szerokości impulsu, obecnie najpopularniejszym trybie przetwarzania, określany jest za pomocą dwóch parametrów: częstotliwości próbkowania oraz rozdzielczości bitowej. Jak słusznie podejrzewacie, czym wyższe te parametry, tym lepsza jakość konwersji i tym wierniejszy brzmieniowo sygnał trafi do komputera w postaci cyfrowej.
Generalną zasadą tego typu konwersji jest próbkowanie, czyli pobieranie próbek materiału analogowego i tworzenie ich reprezentacji cyfrowej. Następuje tutaj interpretacja chwilowej wartości napięcia w sygnale analogowym i przedstawianie jego poziomu pod postacią cyfrową w systemie binarnym (6).
Tutaj jednak na chwilę musimy sobie przypomnieć podstawy matematyki, zgodnie z którymi każda wartość liczbowa może być przedstawiona w dowolnym systemie liczbowym. W całej historii ludzkości stosowano i wciąż stosuje się różne systemy liczbowe. Na przykład na systemie dwunastkowym oparte są takie pojęcia jak tuzin (12 sztuk) czy gros (12 tuzinów, 144 sztuki).
W określeniach czasu używamy systemów mieszanych - systemu sześćdziesiątkowego do sekund, minut i godzin, pochodnego systemu dwunastkowego do określania dni i dób, systemu siódemkowego do dni w tygodniu, systemu czwórkowego (też związanego z systemem dwunastkowym i sześćdziesiątkowym) do tygodni w miesiącu, systemu dwunastkowego do określania miesięcy w roku, a potem już przechodzimy na system dziesiętny, gdzie pojawiają się dekady, stulecia i tysiąclecia. Myślę, że przykład stosowania różnych systemów do wyrażania upływu czasu bardzo dobrze oddaje naturę systemów liczbowych i pozwoli Wam sprawniej poruszać się w zagadnieniach związanych z konwersją.
W przypadku konwersji analogowo-cyfrowej będziemy najczęściej zamieniać wartości wyrażone w systemie dziesiętnym na wartości w systemie dwójkowym. W systemie dziesiętnym dlatego, że pomiar dokonywany dla każdej próbki będzie zwykle wyrażony w mikrowoltach, miliwoltach i woltach. Następnie wartość ta zostanie wyrażona w systemie binarnym, czyli z użyciem dwóch funkcjonujących w nim cyfr - 0 i 1, które reprezentują dwa stany: brak napięcia albo jego występowanie, wyłączony lub włączony, płynie prąd lub nie płynie itd. W ten sposób unikamy przekłamań, a wszystkie działania stają się znacząco prostsze w realizacji poprzez aplikowanie tzw. algorytmów modyfikujących, z czym mamy do czynienia np. w stosunku do wtyczek czy innych procesorów cyfrowych.
Jesteś zerem; albo jedynką
Za pomocą tych dwóch cyfr, zera i jedynki, można wyrazić każdą wartość liczbową, bez względu na jej wielkość. Jako przykład weźmy wyrażoną w systemie dziesiętnym liczbę 10. Kluczem do zrozumienia konwersji systemu dziesiętnego na binarny, dwójkowy, jest to, że cyfra 1 w systemie dwójkowym ma, podobnie jak w systemie dziesiętnym, wartość zależną od swojej pozycji w ciągu liczbowym.
Jeśli 1 znajduje się na końcu ciągu binarnego, to oznacza 1, jeśli na drugiej pozycji od końca, to oznacza 2, na trzeciej oznacza 4, a na czwartej oznacza 8 - w każdym przypadku wyrażone w systemie dziesiętnym. W systemie dziesiętnym ta sama jedynka na końcu oznacza 1, na drugim miejscu od końca oznacza 10, na trzecim 100, a na czwartym 1000 - przykład ten podaję po to, aby zrozumieć analogię.
A zatem jeśli chcemy przedstawić 10 w postaci binarnej, to należy to zrobić, przedstawiając ósemkę oraz dwójkę, czyli zgodnie z tym, co powiedziałem wcześniej, będzie to 1 na czwartym miejscu i 1 na drugim, czyli 1010.
Jeśli mielibyśmy przeprowadzić konwersję napięć od 1 do 10 woltów, bez wartości ułamkowych, czyli z użyciem jedynie liczb całkowitych, to w zupełności wystarczy nam przetwornik, który po stronie binarnej może prezentować ciągi 4-bitowe. 4-bitowe, ponieważ liczba wyrażona w systemie dwójkowym będzie do takiej konwersji wymagać maksymalnie czterech cyfr. W praktyce będzie to wyglądało tak:
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
10 1010
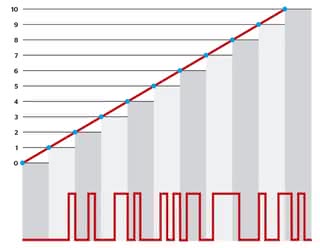
Owe zera na początku dla liczb od 1 do 7 są tylko po to, aby wypełnić ciąg do pełnych czterech bitów i by każda wyrażona binarnie liczba miała taką samą składnię i zajmowała tyle samo miejsca. W formie graficznej taką konwersję liczb całkowitych w systemie dziesiętnym na system dwójkowy prezentuje ilustracja 7.
Zarówno górny jak i dolny przebieg reprezentują te same wartości, z tym że ten pierwszy jest zrozumiały np. dla urządzeń analogowych, choćby liniowych wskaźników poziomu napięcia, a ten drugi dla urządzeń cyfrowych, w tym także komputerów, które właśnie w takim języku przetwarzają dane. Ten dolny przebieg wygląda jak przebieg prostokątny o zmiennym wypełnieniu, czyli różnej proporcji czasowej wartości maksymalnych do wartości minimalnych. W tym zmiennym wypełnieniu jest niejako zakodowana binarna wartość sygnału poddawanego konwersji, stąd nazwa "pulsacyjna modulacja kodu" - Pulse Code Modulation, PCM.
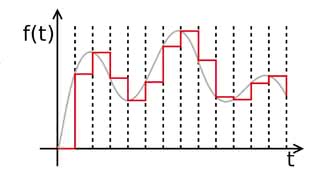
Wracamy teraz do konwersji prawdziwego sygnału analogowego. Wiemy już, że można go opisać linią reprezentującą płynnie zmieniające się poziomy i nie ma w nim czegoś takiego jak skokowe reprezentowanie tych poziomów. Dla potrzeb przetwarzania analogowo-cyfrowego taki proces musimy jednak wprowadzić po to, aby móc co pewien czas mierzyć poziom sygnału analogowego i każdą taką zmierzoną próbkę przedstawiać w postaci cyfrowej.
Przyjęto, że częstotliwość, z jaką te pomiary będą dokonywane, powinna być przynajmniej dwukrotnie wyższa od najwyższej częstotliwości, jaką może człowiek usłyszeć, a ponieważ jest to ok. 20 kHz, stąd najbardziej popularną częstotliwością próbkowania pozostaje 44,1 kHz. Wyliczenie częstotliwości próbkowania związane jest z dość zaawansowanymi działaniami matematycznymi, którymi na tym etapie naszej znajomości technik konwersji nie ma sensu się zajmować.
Więcej, czyli lepiej?
Wszystko to, o czym wspomniałem wyżej, może sugerować, że czym większa częstotliwość próbkowania, czyli dokonywania pomiarów poziomu sygnału analogowego w regularnych odcinkach czasu, tym wyższa jakość konwersji, ponieważ jest ona - przynajmniej w intuicyjnym rozumieniu - bardziej precyzyjna. Czy tak jest naprawdę? O tym przekonamy się za miesiąc.
Tomasz Wróblewski