Krzywe Lissajous piękno drgań

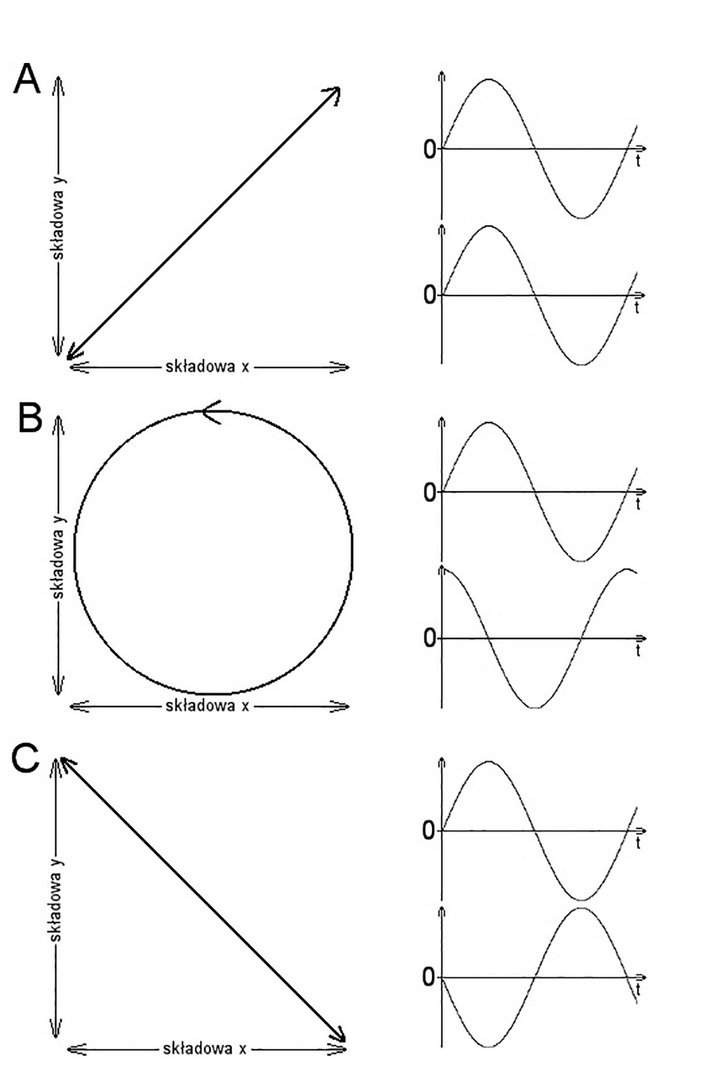
Rozumiem, że powyższy wzór może nie przekonać wszystkich, a w szczególności tych, którzy z jakichś niewiadomych mi powodów czują awersję do opisu matematycznego. Na szczęście, można to też wyjaśnić w sposób graficzny (1). Rysunek ten ukazuje trzy najprostsze przypadki krzywych Lissajous, to jest wtedy, kiedy częstotliwości obu drgań sinusoidalnych zachodzących w prostopadłych do siebie płaszczyznach (składowych x i y) są jednakowe.
Przypadki A, B i C różnią się jednak przesunięciem w fazie, to jest argumentem w w przytoczonym uprzednio wzorze. I tak mamy:
- fazy drgań składowych zgodne (φ = 0) – krzywa jest odcinkiem (1A);
- faza jednego drgania przesunięta względem drugiego o 90º (φ = π/2) – krzywa jest kołem (1B);
- faza jednego drgania przesunięta względem drugiego o 180º (φ = π) – krzywa jest lustrzanym odbiciem odcinka z przypadku A (1C).
Odpowiednio dobierając obie częstotliwości i przesunięcie fazowe, można uzyskać odmienne krzywe, często o zaskakująco estetycznym wyglądzie.
Jak jednak uzyskać takie krzywe, szczególnie, jeśli nie chce się ich po prostu kreślić żmudnie na kartce papieru lub ekranie komputera?
Sposobów jest wiele. Można np. (jak sam Lissajous) obserwować promień światła odbity tajemnic od zwierciadeł, drgających w prostopadłych płaszczyznach. Dobrym sposobem jest też wykorzystanie oscyloskopu, który ma możliwość odchylania plamki zarówno w osi X, jak i Y – wystarczy wtedy podłączyć do urządzenia dwa sygnały elektryczne o regulowanej częstotliwości i fazie.
Wreszcie, do wykreślenia krzywych Lissajous można wykorzystać też właściwości specjalnego wahadła.
Doświadczenie
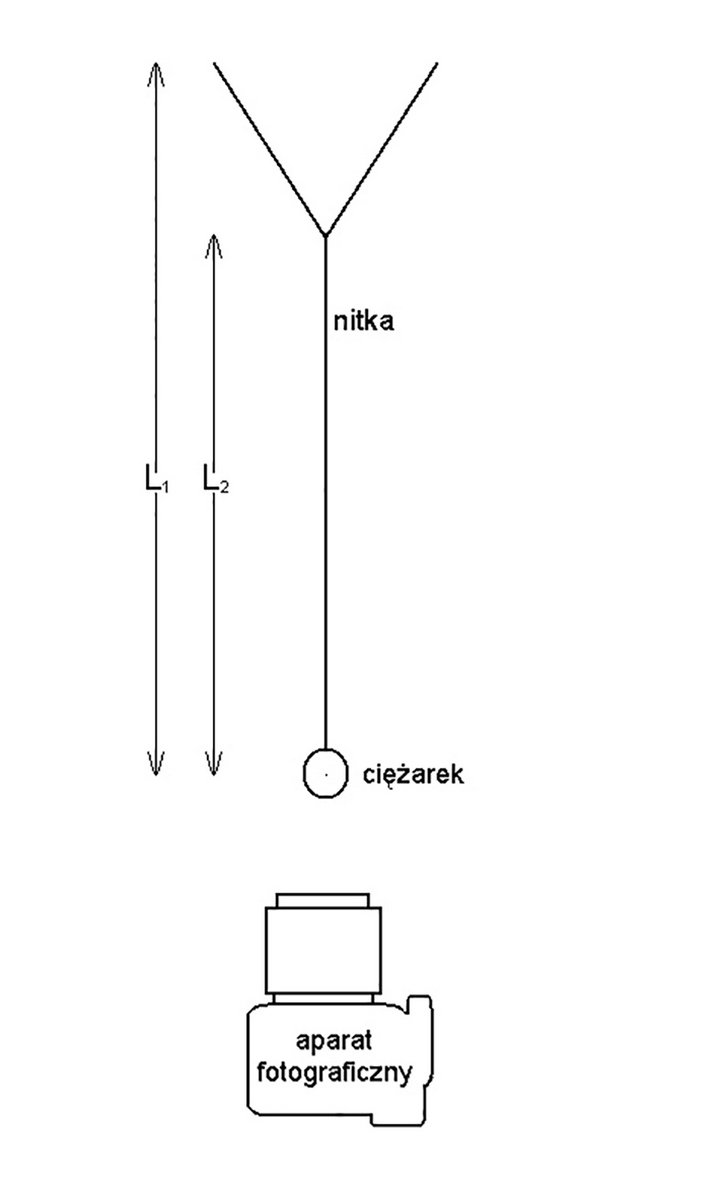
By uzyskać krzywe Lissajous w domowych warunkach, wygodnie jest się posłużyć wahadłem o odpowiedniej konstrukcji (2).
Zastanówmy się, w jaki sposób będzie działało takie wahadło. Wiemy, że dla niewielkich wychyleń okres T drgań wahadła można opisać wzorem:
gdzie:
l – długość wahadła,
g – ziemskie przyspieszenie grawitacyjne. Wahadło o proponowanej konstrukcji w płaszczyźnie prostopadłej do płaszczyzny rysunku będzie wykazywać drgania o okresie T1, zaś w płaszczyźnie rysunku – o okresie T2. Okresy drgań będą się różnić, z powodu różnicy efektywnej długości wahadła w tych płaszczyznach, odpowiednio L1 i L2. Jeśli L2 będzie niewiele mniejsze od L1, to nie zaobserwujemy wyraźnej różnicy częstotliwości drgań. Będzie się natomiast zmieniać wzajemne przesunięcie w fazie (w zakresie od 0 do 2p), ponieważ jedno drganie będzie niejako wyprzedzać drugie. Umożliwi to wykreślenie interesujących krzywych Lissajous.
W moich doświadczeniach długości wahadła wynosiły ok.:
- L1 – 1,40 m
- L2 – 1,30 m
Masa wykorzystanego ciężarka była równa 0,05 kg. Wizualizacji krzywych Lissajous najlepiej dokonać na drodze rejestracji fotograficznej o długim czasie
ekspozycji. Do ciężarka wahadła trzeba wtedy przymocować prosty oświetlacz, zbudowany z diody LED, włączonego szeregowo z nią rezystora (R w zakresie 1-5 kΩ) oraz miniaturowej baterii o napięciu 3V (np. typu CR2032). Aparat fotograficzny powinien być ustawiony poniżej wahadła i skierowany w górę, jak to pokazano na ilustracji 2. Puszczone w ruch wahadło należy wtedy fotografować w ciemności, oczywiście z włączonym oświetlaczem, a czas ekspozycji trzeba dobrać eksperymentalnie. Zwykle będzie to kilkanaście, kilkadziesiąt sekund.
Zarejestrowane w ten sposób obrazy krzywych Lissajous przedstawia ilustracja otwarciowa.
Przy nieco innych długościach L1, L2, a także przy dłuższym czasie naświetlania uzyskano krzywą przedstawioną na ilustracji 3. Widzimy więc, że figury uzyskane nawet w ten bardzo prosty sposób, odznaczają się swoistym, geometrycznym pięknem. Oczywiście, wygląd krzywych można zmieniać w bardzo szerokim zakresie. Trzeba jedynie zmodyfikować długości wahadła, a także długość czasu naświetlania zdjęć. .
Literatura:
Crawford F.C., „Fale”, Warszawa, Wydawnictwo Naukowe PWN, 1973 Gaj J.,
„Laboratorium fizyczne w domu”, Wydawnictwa Naukowo-Techniczne, Warszawa 1985 Taylor C.A.,
„The Art and Science of Lecture Demonstration”, CRC Press, 1988, 50-54.