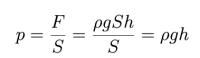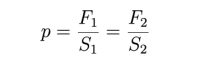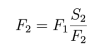Skąd się bierze ciśnienie?

Skąd się bierze ciśnienie?
W normalnych warunkach nie czujemy, że powietrze wywiera na nas ciśnienie. Nie czujemy również, że ma ono masę. A właśnie pojęcie masy jest kluczowe dla wyjaśnienia zjawiska ciśnienia atmosferycznego. Otóż metr sześcienny powietrza, takiego samego, jakim oddychamy na co dzień, waży około 1,2 kilograma!

Ciśnienie atmosferyczne 

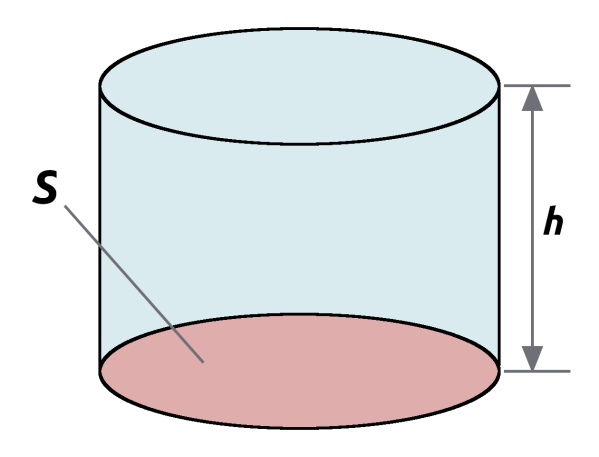
Wyobraźmy sobie słup powietrza o gęstości równej ρ, polu podstawy równym S oraz o wysokości równej h. Masa takiego słupa jest równa iloczynowi jego gęstości i objętości: m = ρV = ρSh. Siła ciężkości działająca na słup dana jest wyrażeniem F = mg, co po podstawieniu masy daje F = ρgS. Ciśnienie jest zdefiniowane jako wielkość siły działającej na powierzchnię do pola tej powierzchni. Wobec tego mamy

co jest matematycznym sformułowaniem prawa Pascala. 

1. Ciśnienie słupa gazu zależy od jego wysokości oraz gęstości.
Zależność tę opisuje prawo Pascala.

Ciśnienie w naczyniu z cieczą

Mechanizm powstawania ciśnienia w płynach jest dokładnie taki sam jak w przypadku gazów. Ciśnienie panujące na dnie oceanów jest równe sumie ciśnienia wywieranego przez słup powietrza oraz przez znajdujący się pod nim słup wody. Podobnie jeśli mamy więcej ośrodków o różnej gęstości, leżących jeden nad drugim.

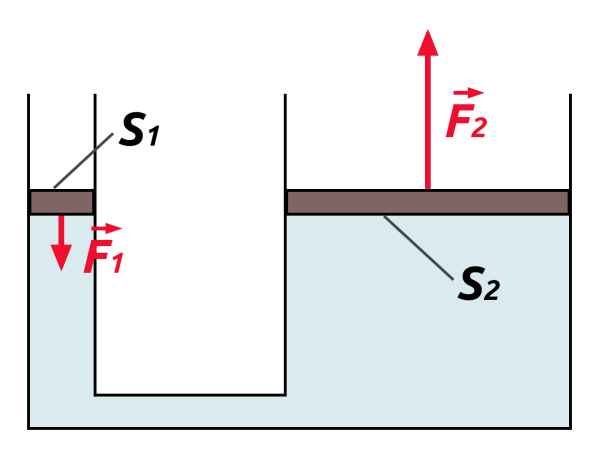
Jeśli chodzi o ciecz zamkniętą w naczyniu, to wywiera ona nacisk nie tylko na dno, ale również na boczne ścianki naczynia. Zjawisko to jest podstawą działania prasy hydraulicznej, którą schematycznie przedstawiono na poniższym rysunku. Działając siłą o wartości F1 na tłok o powierzchni S1, powodujemy, że na wszystkie ścianki naczynia oraz drugi tłok, o powierzchni S2 > S1, działa takie samo ciśnienie. Ponieważ

siła działająca na drugi tłok jest równa

Odrobina historii

Ponieważ nasz gatunek ewoluował w otaczającym nas środowisku, nie odczuwamy w żaden szczególny sposób istnienia ciśnienia atmosferycznego. Dzięki temu przez wiele stuleci nie zdawano sobie w ogóle sprawy z istnienia tego zjawiska. Dopiero w XVII wieku Evangelista Torricelli, próbując udoskonalić działanie pompy głębinowej, odkrył, że istnieje ciśnienie atmosferyczne i wywiera wpływ na to urządzenie.

Torricelli skonstruował również pierwszy barometr cieczowy, pozwalający na pomiar wartości ciśnienia atmosferycznego. Kilka lat później Blaise Pascal, zainspirowany pracami Torricellego, sprecyzował pojęcie ciśnienia i sformułował równanie opisujące zależności ciśnienia atmosferycznego od wysokości słupa powietrza.

2. Zasada działania prasy hydraulicznej. Działając na mniejszy tłok pewną siłą,
generujemy siłę o większej wartości działającą na drugi z tłoków

Sprawdź swoją wiedzę

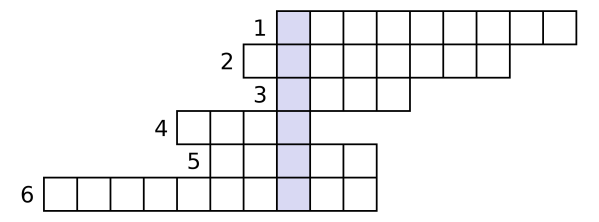
Rozwiąż krzyżówkę i przekonaj się, ile udało ci się zapamiętać z tekstu. Litery w zaznaczonych polach utworzą hasło - nazwę jednostki ciśnienia w układzie SI.

1. Wywiera nacisk na powierzchnię Ziemi
2. Służy do pomiaru ciśnienia
3. … ciężkości, działa na każde ciało obdarzone masą
4. Za jego pomocą możemy zwiększyć ciśnienie w naczyniu z cieczą
5. …hydrauliczna
6. Nazwisko odkrywcy ciśnienia atmosferycznego

Propozycja doświadczenia

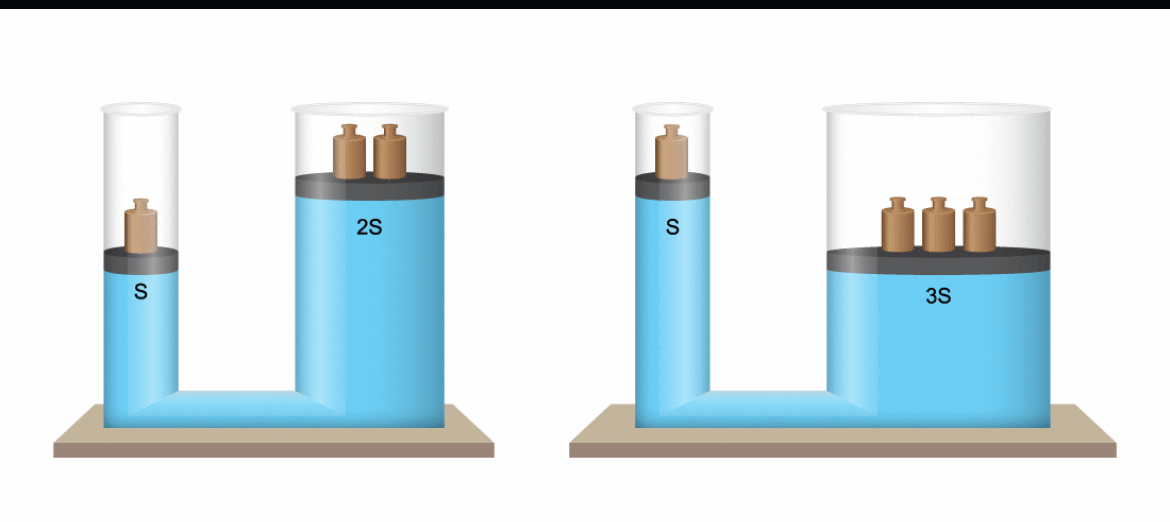
W celu wyznaczenia wartości ciśnienia wywieranego przez słup cieczy (oraz udowodnienia, że zależy ono od jej gęstości) możemy posłużyć się naczyniami połączonymi. Mogą to być rurki w kształcie litery U zamocowane na stabilnych podstawach i zaopatrzone w podziałki. Warto przygotować przynajmniej kilka zestawów doświadczalnych na klasę, choć najlepiej byłoby, żeby uczniowie pracowali w parach.

Do rurki nalewamy tyle wody, aby sięgała powyżej zakrzywionej części naczynia. Następnie do jednego z ramion wlewamy olej jadalny. Posługując się skalą, odczytujemy poziom obu cieczy. Znajdujemy ich gęstość w tablicach, a następnie wszystkie dane podstawiamy do wzoru opisującego prawo Pascala. Wyniki uzyskane dla obu cieczy powinny być zgodne w granicach błędu pomiarowego.

Warto poświęcić nieco czasu na przedyskutowanie w klasie wpływu dokładności pomiaru wysokości słupa cieczy na niepewność uzyskanego wyniku. Zazwyczaj szacowanie błędów sprawia uczniom spore problemy, a jego metodologia nie jest dla nich zrozumiała.

Dla nauczyciela

Niniejszy materiał można wykorzystać w szkole podstawowej do realizacji punktów podstawy programowej dotyczących prawa Pascala, w szczególności: V.5, V.6 oraz V.9.2. Ze względu na obszerny opis umiejętności uczniów wymaganych tymi punktami, ich treść nie została tu przytoczona. Warto jedynie dodać, że również w szkole ponadpodstawowej niektóre programy nauczania przewidują powtórzenie zagadnień z hydrostatyki, zatem nauczyciel ma różne możliwości wykorzystania treści zawartych w tym artykule. 

Joanna Borgensztajn

 

Pozostałe artykuły
Budujemy aerostaty, czyli o tym, jak zbudować latający model balonu napełniany ogrzanym powietrzem Budujemy aerostaty, czyli o tym, jak zbudować latający model balonu napełniany ogrzanym powietrzem
Statki powietrzne, tak nazywają się obiekty latające w atmosferze i skonstruowane przez człowieka, dzielą się na aerodyny, które latają dzięki dynamicznemu oddziaływaniu powietrza na ...
0
Bardzo proste modele latające wykonane z piankowych podkładów pod panele Bardzo proste modele latające wykonane z piankowych podkładów pod panele
MiniMini to bardzo prosty latający model szybowca do wykonania z pianki pod panele podłogowe (depron). Model można puszczać zarówno w domu, jak i na zewnątrz.
0
Wicherek 0,10 - czyli latający model słynnego polskiego latającego modelu! Wicherek 0,10 - czyli latający model słynnego polskiego latającego modelu!
Inspiracją do tego opracowania jest kultowy model „Wicherek”, można powiedzieć opus dei legendy polskiego modelarstwa - Wiesława Schiera. Jest to najbardziej znana konstrukcja modelarsko-lotnicza ...
0
AVT5599. Zdalnie sterowany włącznik 4-kanałowy AVT5599. Zdalnie sterowany włącznik 4-kanałowy
Urządzenie umożliwia zdalne włączanie/wyłączanie czterech urządzeń za pomocą typowych pilotów na podczerwień od sprzętu powszechnego użytku. Jego niewątpliwym atutem jest możliwość ...
0