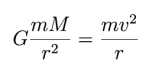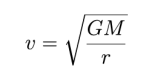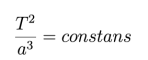Siła grawitacji jako przyczyna ruchu ciał niebieskich - część 2

Siła grawitacji jako siła dośrodkowa Porównując wzór na siłę grawitacji ze wzorem na siłę dośrodkową, dostajemy
Dzieląc to wyrażenie obustronnie przez masę satelity i odpowiednio przekształcając, wyprowadzamy wzór na jego prędkość na orbicie:
Jak wynika z tego wzoru, prędkość zależy wyłącznie od masy ciała centralnego oraz promienia orbity.
Prawa Keplera
Kepler sformułował prawa opisujące ruch planet w Układzie Słonecznym. Zgodnie z pierwszym z nich każda planeta porusza się po orbicie eliptycznej, a Słońce znajduje się w jednym z ognisk tej elipsy. Oczywiście prawo to nie uwzględnia obiektów jednorazowo przelatujących w okolicach naszej gwiazdy dziennej i poruszających się po trajektoriach otwartych.
Drugie prawo stwierdza, że w jednakowych odstępach czasu promień wodzący planety zakreśla równe pola. Warto zauważyć, że prowadzi to do zmiany prędkości ciała na orbicie. Do tego samego wniosku doszlibyśmy również, powołując się na zasadę zachowania momentu pędu.
Trzecie prawo wiąże okres obiegu planety z długością wielkiej półosi jej orbity:
Wielkość ta jest stała dla wszystkich obiektów okrążających to samo ciało centralne i zależy wyłącznie od masy tego ciała. Nie zależy ona od mas planet ani od ich rozmiarów geometrycznych.
Sprawdź swoją wiedzę - ćwiczenie rachunkowe
Planeta porusza się wokół gwiazdy o masie M po okręgu o promieniu r. Znajdź wyrażenie na wartość
dla tej planety. Wskazówka: porównaj wzór na prędkość w ruchu po okręgu ze wzorem na prędkość satelity na orbicie.
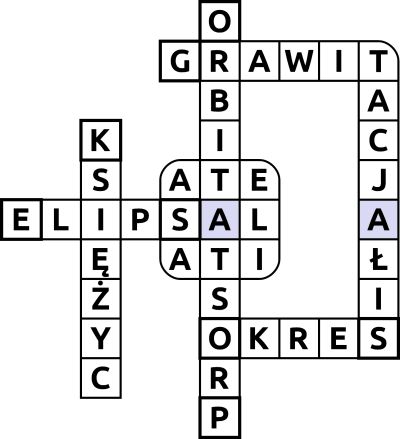
Jolka
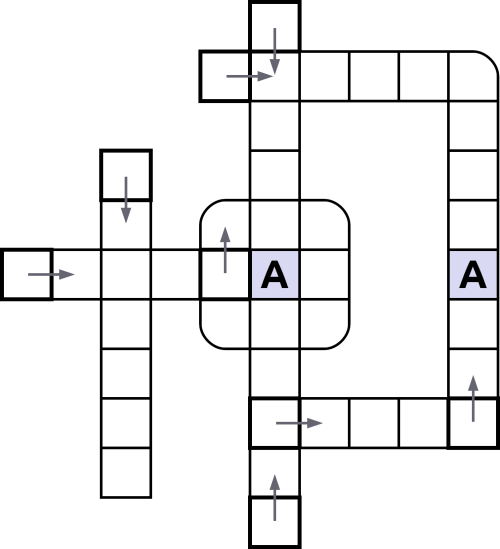
Na podstawie opisów pod krzyżówką znajdź hasła, które należy wpisać w pola. Pierwszą literę hasła należy umieścić w pogrubionej kratce, a następnie wpisać słowo zgodnie z kierunkiem strzałki. Napotykając pole z zaokrąglonym narożnikiem, należy kontynuować wpisywanie tekstu zgodnie z jego nowym kierunkiem. Znaki w szarych polach są wspólne dla kilku haseł i stanowią ostatnią literę każdego z nich.
- kształt orbity opisany jednym z praw Keplera
- obiekt krążący bez napędu wokół ciała centralnego
- linia, wzdłuż której spada ciało wyrzucone pionowo w górę
- na przykład dośrodkowa
- oddziaływanie pomiędzy ciałami obdarzonymi masą
- inna nazwa naturalnego satelity
- inna nazwa trajektorii, po której porusza się satelita
Projektujemy układ satelitów
Projekt najlepiej zrealizować na lekcji, pracując w niewielkich grupach. Każda grupa wybiera jeden obiekt astronomiczny, wokół którego będą krążyć satelity. W przypadku dobrze znanych obiektów łatwo znaleźć w rzetelnych źródłach informacje o ich masach oraz rozmiarach.
Układ satelitów można zaprojektować na jeden z dwóch sposobów. Pierwsza metoda polega na tym, że dla wybranych orbit, większych od promienia ciała centralnego, należy obliczyć okresy obiegu poszczególnych ciał. Pracując drugim sposobem, postępujemy odwrotnie: dla wybranych okresów obiegu liczymy promienie orbit.
Uczniowie powinni podzielić się pracą w taki sposób, aby każdy z nich wykonał obliczenia przynajmniej dla jednego satelity. Poprawność rachunków dosyć łatwo samodzielnie zweryfikować, sprawdzając, czy wyniki uzyskane dla układu satelitów spełniają trzecie prawo Keplera. Warto zaproponować uczniom ciekawy sposób prezentacji wyników (być może w formie
pracy domowej?), taki jak na przykład wykonanie rysunku lub modelu.
Dla nauczyciela
Opisane w niniejszym artykule zagadnienie można wykorzystać na lekcji fizyki w liceum lub technikum w zakresie rozszerzonym do realizacji poniższych punktów podstawy programowej: IV.4 (uczeń) wskazuje siłę grawitacji jako siłę dośrodkową w ruchu po orbicie kołowej, oblicza wartość prędkości na orbicie kołowej o dowolnym promieniu; omawia ruch satelitów wokół Ziemi; IV.5. interpretuje III prawo Keplera jako konsekwencję prawa powszechnego ciążenia; stosuje do obliczeń III prawo Keplera dla orbit kołowych.
Joanna Borgensztajn
Rozwiązanie zadań: Minitest: 1.C, 2.D, 3.D, 4.A.
Ćwiczenie rachunkowe: 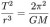
Zobacz także:
Siła grawitacji jako przyczyna ruchu ciał niebieskich - część 1