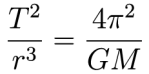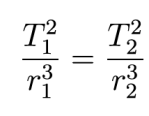Prawa Keplera - zbieg okoliczności czy prawo przyrody?

Kepler sformułował prawa dotyczące ruchu planet na podstawie wieloletnich obserwacji położenia Marsa na niebie, zarówno własnych, jak i prowadzonych przez jego poprzedników, w szczególności przez Tychona Brahe. Po dokładnej rekonstrukcji graficznej wzajemnego położenia Marsa, Ziemi i Słońca okazywało się, że prawidłowe wyjaśnienie wyników obserwacji uzyskujemy wówczas, gdy Słońce znajdzie się w centrum Układu Słonecznego, a Ziemia i Mars okrążają je po elipsach.

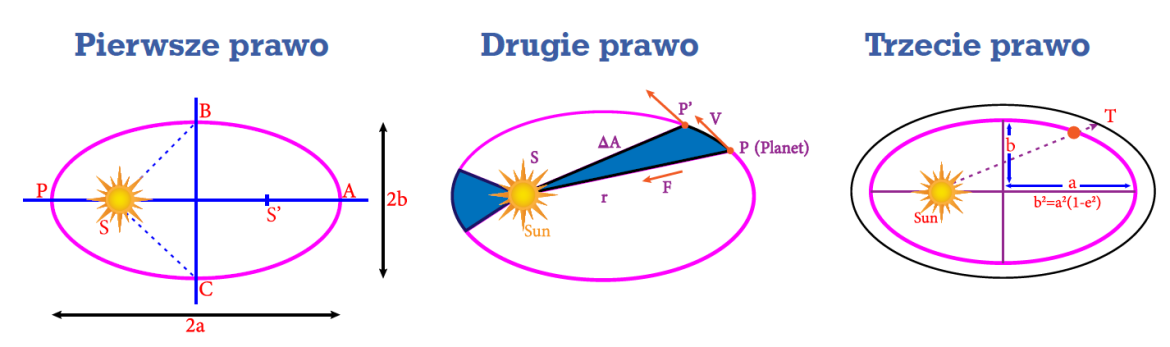
Wyjaśnienie pierwszego prawa Keplera

Zgodnie z prawem powszechnego ciążenia dwa ciała obdarzone masą przyciągają się siłą grawitacji proporcjonalną do iloczynu ich mas oraz odwrotnie proporcjonalną do kwadratu odległości. Jeśli uwzględnimy fakt, że zarówno satelita, jak i ciało centralne obiegają wspólny środek masy, to analiza ich ruchu w oparciu o prawo zachowania energii i prawo zachowania pędu prowadzi do wniosku, że mniejsze ciało porusza się po krzywej stożkowej.

Parametry tej krzywej zależą między innymi od odległości tych ciał od ich środka masy oraz prędkości względem tego punktu. Tak więc możliwe okazują się zarówno zamknięte orbity eliptyczne, jak i otwarte orbity paraboliczne czy hiperboliczne. Istnienie orbit otwartych stwierdzono, analizując trajektorie obiektów pochodzących spoza Układu Słonecznego, które jednorazowo przelatują w okolicach dostępnych do obserwacji.

Wyjaśnienie drugiego prawa Keplera

Drugie z praw opisujących ruch planet na orbicie można wyjaśnić bezpośrednio na podstawie zasady zachowania momentu pędu. Skoro moment pędu izolowanego układu dwóch ciał jest stały, to oddalając się od Słońca, planeta zwiększa swoją prędkość na orbicie. Najszybciej porusza się w punkcie najbardziej oddalonym od Słońca, a najwolniej – w oddalonym najmniej.

Wyjaśnienie trzeciego prawa Keplera

Jeśli przyjmiemy, że w ruchu planety po okręgu siła grawitacji pełni funkcję siły dośrodkowej i porównamy wzory na te siły, dostaniemy wyrażenie

Czynnik

zależy jedynie od masy ciała centralnego, dlatego ma wartość stałą dla wszystkich jego satelitów. Znając okres obiegu ciała na orbicie, można oszacować średni promień tej orbity.

Na podstawie tych danych można z kolei wyznaczyć promień orbity lub okres obiegu innej planety, pod warunkiem że znamy jedną z tych dwóch wielkości. W podręcznikach szkolnych trzecie prawo Keplera jest zazwyczaj wykorzystywane w tym drugim celu i zapisywane jako

Zastosowanie praw Keplera

Zapewne nietrudno się domyślić, że prawa Keplera możemy stosować zarówno do planet Układu Słonecznego, ich naturalnych księżyców, jak również sztucznych satelitów Ziemi. Czy jednak możemy zastosować je w przypadku egzoplanet krążących wokół odległych gwiazd? Jeżeli ktoś ma pokusę, aby udzielić odpowiedzi przeczącej (bo przecież nie obserwujemy egzoplanet wizualnie), to niestety jest w błędzie.

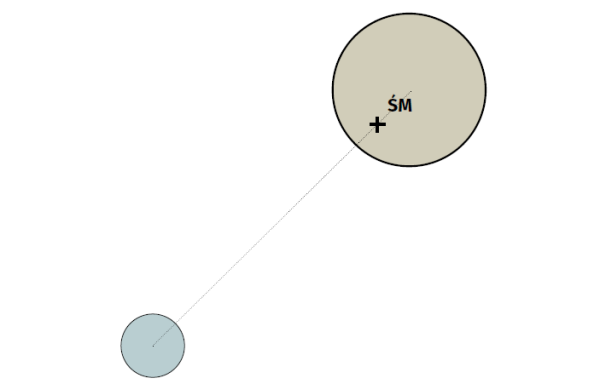
Dzięki połączeniu różnych technik obserwacyjnych i praw Keplera można z dużym prawdopodobieństwem określić masę niewidocznego obiektu krążącego wokół innej gwiazdy, promień jego orbity i okres obiegu. Jedną z metod jest bardzo precyzyjny pomiar położenia tarczy gwiazdy na tle innych gwiazd, znacznie bardziej odległych od Ziemi. Jeżeli gwiazda posiada układ planetarny, to jej tarcza będzie krążyć wokół środka masy układu. Do wyników obserwacji można następnie dopasować odpowiedni model systemu planetarnego.

1. Jeśli gwiazdę okrąża masywna planeta, to jest możliwe zaobserwowanie ruchu gwiazdy
wokół środka masy układu. Zmienia się wówczas położenie gwiazdy na tle dalszych obiektów

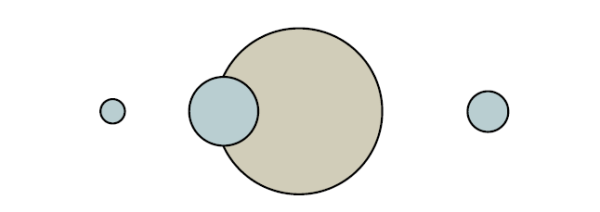
Również zmiana jasności gwiazdy może wskazywać na obecność planet, okresowo przysłaniających jej tarczę. Szczególnie w sytuacjach, w których nie ma innego wyjaśnienia obserwowanego zjawiska. Także w tej sytuacji precyzyjne pomiary pozwalają na określenie okresu obiegu planety wokół gwiazdy oraz oszacowanie jej masy i promienia orbity.

2. Obecność jednej lub kilku planet możemy stwierdzić, obserwując cykliczne
zmiany jasności gwiazdy spowodowane przysłanianiem jej tarczy

Sprawdź swoją wiedzę - zadanie rachunkowe

Oszacuj, na jakiej wysokości od powierzchni Ziemi należy umieścić satelitę geostacjonarnego. Dla uproszczenia przyjmij, że promień Ziemi wynosi 6400 km, odległość od środka Ziemi do środka Księżyca wynosi 380 000 km a okres obiegu Księżyca wokół Ziemi to 27 dni.

Dla nauczyciela

Powyższy materiał można wykorzystać na lekcji fizyki w szkole ponadpodstawowej w zakresie rozszerzonym do realizacji punktów podstawy programowej dotyczących analizy ruchu ciał po orbitach, w szczególności punktów IV.3, IV.5 i IV.6.

Joanna Borgensztajn

Zadanie rachunkowe
Przybliżona odległość satelity geostacjonarnego od powierzchni Ziemi to około 35 600 km.