Dzielenie "na pół"

Z dzieleniem są kłopoty. W średniowieczu sposób pisemny dzielenia był tak skomplikowany, że nazwano to "sposobem galernika". Dzisiaj, w nauczaniu początkowym, dydaktycy zwracają uwagę na dwa rodzaje dzielenia. Jest to "dzielenie na" oraz "dzielenie przez" (przeczytaj również o liczbach pierwszych), inaczej nazywane dzieleniem przez podział i dzieleniem przez mieszczenie. Jeżeli mam rozdać 391 kartek 23 uczniom, to mogę najpierw obliczyć, po ile kartek dam każdemu. Wykonuję stosowne dzielenie: 391 : 23 = 17 i każdemu daję po 17 kartek. Można to jednak zrobić bez obliczeń. Chodzę po klasie i daję każdemu po jednej kartce, potem każdemu daję drugą i tak dalej. W ten sposób nie muszę wiedzieć, ilu jest uczniów i po ile kartek daję. Jeżeli rzeczywiście na egzaminie uczniowie dostają kilka oddzielnych kartek, ten pierwszy sposób jest mniej sprawiedliwy: ci, którzy siedzą na końcu, otrzymują wszystko później niż ci z początku.
Pewne problemy natury matematycznej (a co najmniej logicznej) powstają, gdy chcemy zachować równowagę i sprawiedliwość w różnych grach. Jak wiemy, gdy w meczu piłki nożnej jest remis, a trzeba koniecznie wyłonić zwycięzcę, wówczas dochodzi do dogrywki i jeśli ta nie przynosi rozstrzygnięcia, zawodnicy strzelają karne, z jedenastu metrów (w zasadzie nie są to już rzuty karne, bo nie dyktuje się ich za karę, ale nie przejmujmy się tym). Po losowaniu kolejności wykonywania "jedenastek" sytuacja jest niesymetryczna: ci, którzy strzelają pierwsi, mają przewagę psychologiczną. W tenisie jest bardziej sprawiedliwie: pierwszy gracz serwuje raz, a potem każdy po dwa razy.
Pisząc o tym, przypominam sobie zdumiewający algorytm, jaki stosowaliśmy (my, chłopcy kilkunastoletni) dawno temu, gdy trzeba było podzielić się na dwie drużyny. Wybierano najpierw dwóch kapitanów (przez aklamację), a ci losowali, kto zaczyna dobierać graczy. Pierwszy wskazywał gracza, a drugi decydował, do której drużyny on trafia - potem drugi wybierał, a pierwszy przydzielał. Było to "strasznie psychologiczne" - jeśli pierwszy wskazałby najlepszego na podwórku Kocia (przezwisko autentyczne), drugi natychmiast wziąłby go sobie, a jeśli najgorszego - przydzieliłby go do pierwszej drużyny.
Tyle o podziale na dwie części, na dwie klasy. Źle, gdy w życiu widzimy wszystko biało-czarno… Obecnie mówi się "zero-jedynkowo". Tak się wyraził ("widzę zero-jedynkowo") w pewnej sytuacji jeden z naszych byłych prezydentów i z kontekstu było widać, że rozumie, o co chodzi - co nie zdarza się często politykom. Wracajmy jednak do matematyki.
Linie sprawiedliwości
Dwa kwadraty albo dwa koła możemy przepołowić jedną linią. Wystarczy połączyć środki - wyrażając się ściślej, linią połowiącą obie figury jest linia prosta przechodząca przez ich środki. Dla trójkątów jest już trudniej. Trójkąt równoboczny ma środek, ale nie każda prosta przechodząca przez ten środek dzieli trójkąt na połowy. "Środek" trójkąta nie jest bowiem jego środkiem symetrii.
O takich prostych zagadnieniach pisałem wcześniej temu. Warto zauważyć pewne zastosowanie. Przepisuję z pierwszej polskiej książki o matematyce popularnej - "Lilavati" (pierwsze wydanie rok 1928), autorstwa Szczepana Jeleńskiego:
Dwóch ogrodników spierało się o zawartość beczki, chodziło o rozpuszczenie w niej soli potasowych. Jeden z nich twierdził, że w beczce wody jest więcej niż połowa, drugi obstawał, że jest mniej. Jak się przekonać, kto ma rację, nie używając ani patyka, ani sznurka, ani niczego, co by mogło służyć do pomiaru? Mamy przed sobą nie żart matematyczny, lecz prawdziwe geometryczne zadanie, chociaż rozwiązanie jest śmiesznie łatwe. A jednak rozwiązywanie podobnych zadań warte jest, by nad nimi trochę pomyśleć.
Oto ono. Jeśli by beczka była istotnie równo do połowy napełniona wodą, to nachyliwszy beczkę tak, żeby powierzchnia wody dosięgła brzegu beczki, zobaczylibyśmy, że wyższy punkt dna znajduje się również na powierzchni wody. Wypływa to stąd, że płaszczyzna przeprowadzona przez diametralno przeciwległy punkt górnego i dolnego obwodu beczki dzieli ją na dwie równe części. Jeśli wody jest mniej niż połowa beczki, to przy takim pochyleniu musi wystąpić z wody fragment dna. Wreszcie, jeśli wody jest więcej niż połowa beczki, to całe dno pozostanie pod wodą.
Nietrudno przekonać się, że każdy obszar możemy podzielić prostoliniowym cięciem na dwie części o równym polu.
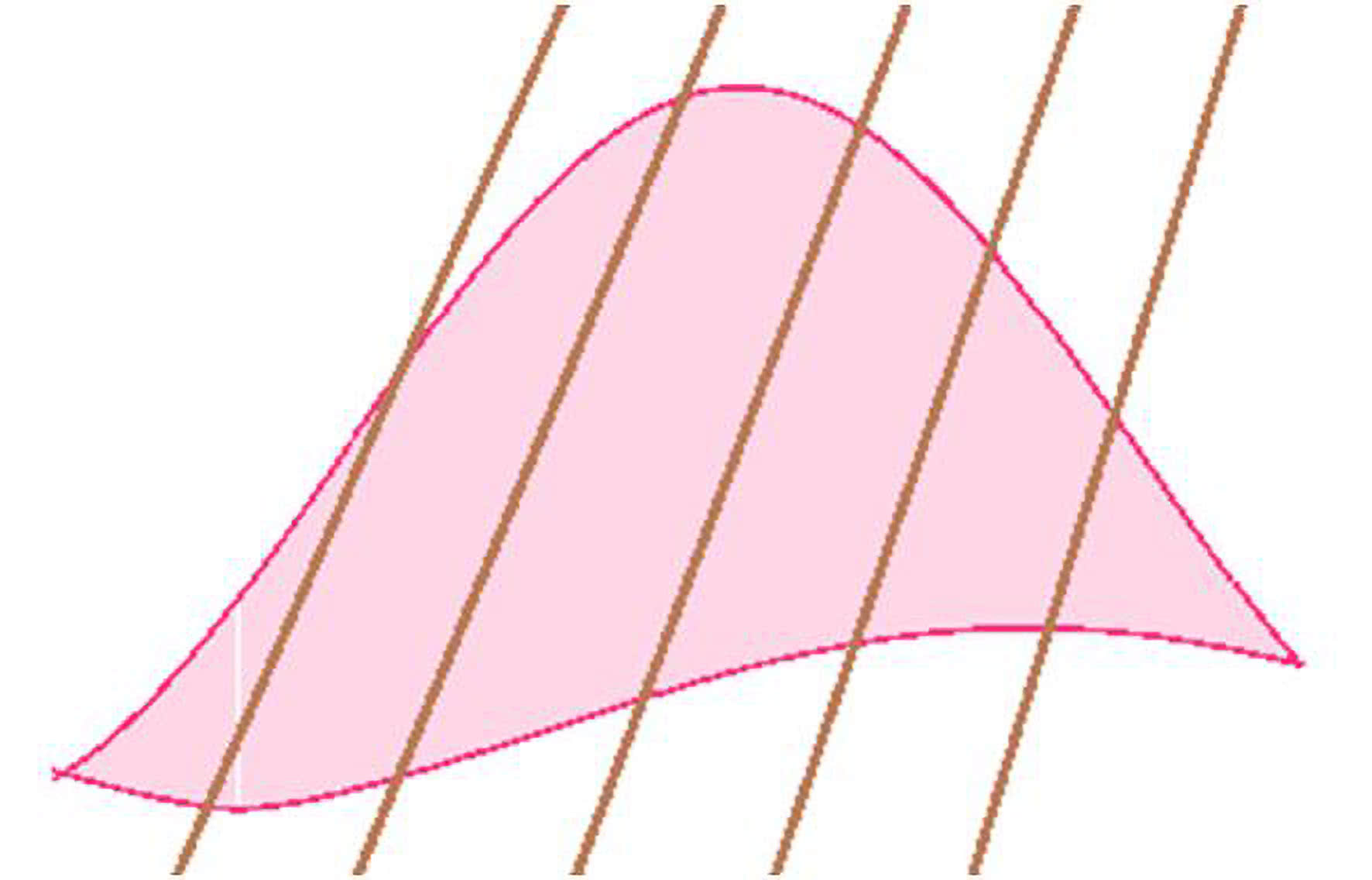
Na rys. 1 widzimy nieregularny obszar. Próbujemy go podzielić na dwie równe części - to znaczy równe co do pola. Przesuwamy linię prostą np. z lewa na prawo - w pewnym położeniu pola "po lewej" i "po prawej" staną się równe. Nie mamy wątpliwości, że tak będzie. Jeżeli rankiem był mróz, a w południe odwilż, to w pewnym momencie na termometrze musiało być zero stopni, prawda?
Wykorzystujemy tu ważne pojęcie matematyczne, a w zasadzie filozoficzne: ciągłość. Wyobrażamy sobie, że czas płynie jak rzeka, nieprzerwanym strumieniem - nie tak, jak na niektórych zegarach (dawniej często spotykanych na dworcach kolejowych), gdzie wskazówka minutowa poruszała się skokowo, co minutę. W teoriach fizycznych dotyczących mikroświata pojęcie czasu zmieniającego się skokowo jest dopuszczalne. Nie możemy sobie jednak tego wyobrazić ludzkim umysłem: co się dzieje, gdy czas przez chwilę nie płynie?
Ciągłe są - według naszych wyobrażeń - długość, a zatem wysokość i szerokość. Tu już wiemy, że to nieprawda, bo wszyscy składamy się z atomów. Atomy są jednak tak malutkie, a nasz umysł jest tak przyzwyczajony do ciągłości, że bez trudu pojmujemy, iż może być odcinek o długości, powiedzmy, pi metrów. To znaczy, że w przybliżeniu to 3,14 m, w lepszym przybliżeniu 3,1415926, a "dokładnie" tego nigdy nie da się wyrazić. Nieskończoność wcale nas nie przeraża.
Wracajmy do głównego tematu: podziału na dwie części. Rozumowanie, które opisałem, można wykorzystać, gdy dwóch spadkobierców chce sprawiedliwie podzielić odziedziczone pole. "Sprawiedliwie" znaczy trochę co innego niż "równe co do pola" - bo może być przecież tak, że zachodnia część jest bardziej atrakcyjna niż wschodnia.
Wtedy część wschodnia może (a nawet powinna) być większa, aby równoważyć zalety zachodniej. Nie trzeba w tym celu przeprowadzać skomplikowanej wyceny eksperckiej. Po prostu pierwszy spadkobierca rysuje na mapie proponowaną linię podziału. Jasne, że poprowadzi ją tak, by subiektywna wartość jego części była co najmniej połową wartości całości. Jeżeli drugi uważa, że tamten wziął sobie za dużo, przesuwa granicę. Pierwszy znów może ją skorygować. Postępowanie trwa do momentu, gdy obaj zgodzą się na ostateczny przebieg granicy.
Sposób ten działa bardzo dobrze, jeżeli w żadnej części nie znajduje się rzecz niepodzielna (dom, źródło, szczególnie ładny dąb). Wtedy… trzeba zastosować inną metodę. Prawie zawsze wszystko da się przeliczyć na pieniądze. Tak, jasne, że "prawie" robi różnicę. To jednak szczęście, że nie wszystko da się wyrazić w jednostkach monetarnych. Ale ten artykuł nie jest traktem filozoficznym o szczęściu.
Linie proste na rys.1 mogliśmy prowadzić w dowolnym kierunku. A zatem: dla każdego obszaru płaskiego i każdego kierunku istnieje linia prosta, dzieląca ten obszar na dwie części o równych polach. To proste i ciekawe twierdzenie. Nieświadomie wykorzystujemy tu zaawansowany aparat analizy matematycznej (tzw. twierdzenie Bolzano: każda funkcja ciągła na zbiorze zwartym przyjmuje wszystkie wartości między swym maksimum i minimum). Można to ująć inaczej: linie ciągłe nie mogą przenikać się wzajemnie, nie mając punktów wspólnych. Ciekawym zastosowaniem tej zasady jest rozwiązanie takiego oto zadania:
Na dalekim, dzikim zachodzie Stanów Zjednoczonych, między miasteczkami Kentucky Raw Chicken a Chickenburger kursuje jeden pociąg. Jednego dnia startuje o godz. 8 rano z KRC i na godz. 8 wieczorem jest w Chickenburger. Następnego dnia jedzie z powrotem. Ma zmienną prędkość, jako że jego trasa wiedzie przez góry i niziny. Proszę wykazać, że jest taki punkt, w którym pociąg jest zawsze o tej samej porze, co poprzedniego dnia.
Rozwiązanie okazuje się banalnie proste. Wyobraźmy sobie, że linię rozszerzono do trakcji dwutorowej i pociąg kursuje codziennie. Jeden skład mknie w jedną stronę i następnego dnia rusza z powrotem. W pewnym punkcie mija się z drugim składem.
Zadanie to przyszło mi do głowy, gdy za studenckich czasów jechałem pociągiem na wycieczkę do Bułgarii. Wyliczyłem sobie, gdzie w Rumunii miniemy się z pociągiem powrotnym. Stałem na korytarzu i wypatrywałem. W pewnej krótkiej chwili wyczekiwany obiekt tylko mignął za oknem! Mieliśmy przecież prędkość względną ponad 200 km/godz. Tym niemniej poznałem, że to polski "dualny" pociąg. Wracali nim opaleni już wczasowicze, wypluskani w Morzu Czarnym.
O matematyce przy kanapkach
A co z dzieleniem na czworo? Koło i kwadrat łatwo. Młodzi Czytelnicy na pewno sprawnie dzielą pizzę na równe kawałki - jeśli amatorów jest pięcioro, to łatwiej dzielić kolistą niż kwadratową, prawda?
Twierdzenie. Dowolny obszar można podzielić na cztery części o równych polach dwiema prostymi prostopadłymi.
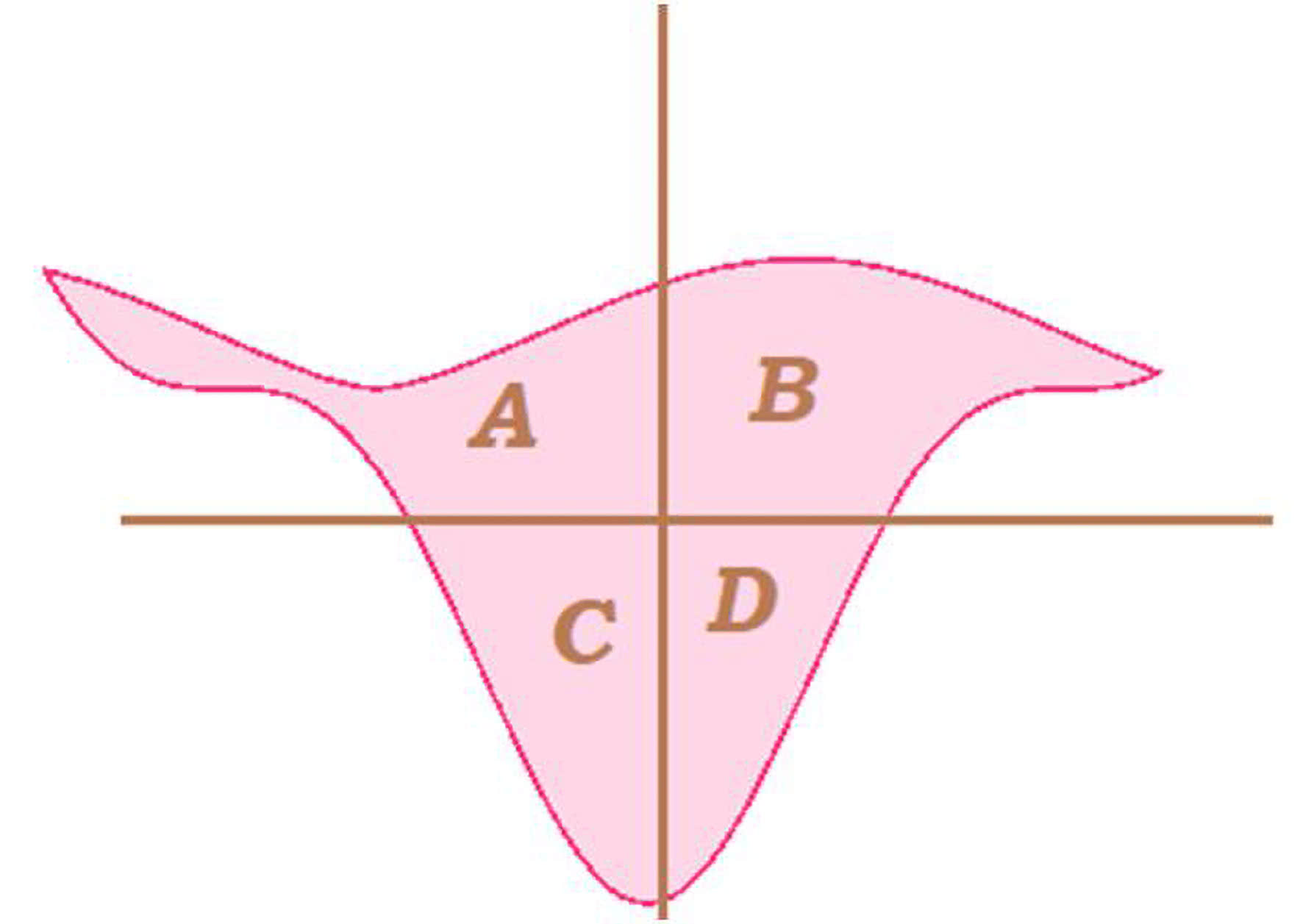
Oto dowód. To ładne rozumowanie. Dla każdego kierunku wybierzmy prostą połowiącą obszar. Niech kąt między tym kierunkiem a osią x będzie równy a. Następnie podzielmy obszar na połowy za pomocą prostej prostopadłej do poprzedniej. Wcale nie ma gwarancji, że utworzyły się cztery równe ćwiartki (2).
Wiemy tylko, że A + B = C + D oraz A + C = B + D. Z tego jednak wcale nie wynika, że A = B = C = D, bo mogło by być np. tak: A = 5, B = 3, C = 3, D = 5. Rozpatrzmy funkcję, która kątowi a przyporządkowuje różnicę A - B. Jeśli ta funkcja nie zeruje się na krańcach przedziału [0, 90°], to ma w tych końcach przeciwne znaki - a zatem gdzieś musi być miejsce zerowe. Wtedy A = B, a w konsekwencji C = D.
To ciekawe rozumowanie i twierdzenie egzystencjalne: wiemy, że jest takie położenie, a nie wiemy, jak znaleźć. Czy jednak aby na pewno nie umiemy? Zmieniamy kąt i obserwujmy różnicę A - B. Gdy będzie równa zero, mówimy "stop". To nasze rozwiązanie, nasz punkt równowagi.
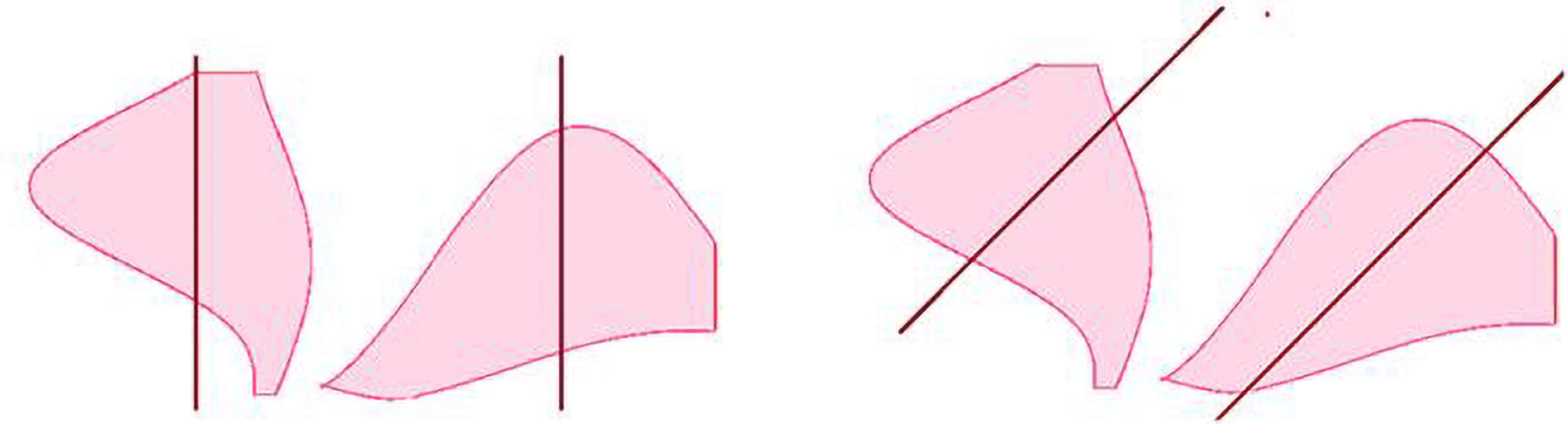
Weźmy teraz dwa obszary (3). Zawsze istnieje jedna linia prosta, dzieląca oba na dwie równe części. Rozumowanie jest bardzo podobne. Dla każdego kierunku ustalamy proste połowiące każdy z tych obszarów. Zmieniamy łagodnie kierunek, w pewnym momencie proste się zejdą.
Interesujące, że odkrywcy podobnego twierdzenia w wymiarze 3 nazwali je twierdzeniem o kanapkach. Sformułowanie przepisuję ze słynnej książki Hugona Steinhausa (1887-1972, matematyka lwowskiego, a potem wrocławskiego) "Kalejdoskop Matematyczny" (pierwsze wydanie 1938 r.): zawsze można bułkę z masłem i szynką przekroić płaskim cięciem tak, by przepołowić bułkę, masło i szynkę.
Odkrywcami tego faktu byli Stefan Banach i Hugo Steinhaus, ok. 1933 r. Potem to samo odkryli matematycy amerykańscy Arthur H. Stone i John Tukey w roku 1942, kiedy polscy uczeni mieli już zgoła inne kłopoty na głowie… Stało się to, co się często dzieje: twierdzenie nie nosi nazwiska odkrywcy, tylko tego, kto je spopularyzował. Nie ma w tym na ogół niczyjej złej woli, ale krzyczeć o swoje trzeba.
Tu dygresja o nauczaniu matematyki. Odbywa się ono głównie metodą "zadanie - rozwiązanie". Nauczyciel daje konkretne zadanie, uczeń rozwiązuje je wyuczoną metodą. Marzy mi się zawsze coś innego. Nie dajemy zadania, tylko ogólny problem i sugerujemy metodę.
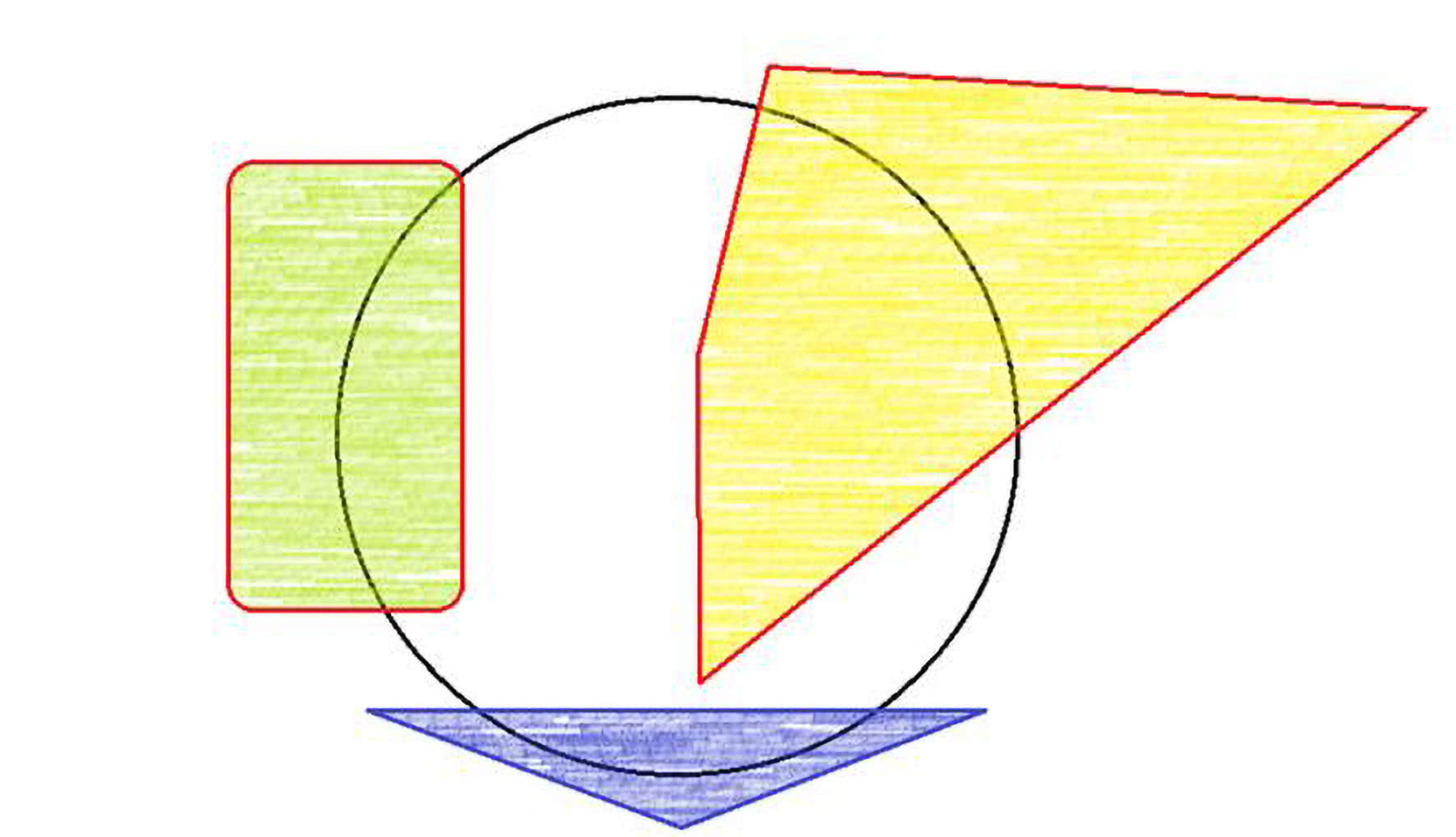
Oto przykład: Prześledź rozumowanie, dające rozwiązanie zadania o kanapkach (w przypadku płaskim często nazywamy to twierdzeniem o naleśnikach). Znajdź trzy obszary płaskie, których się nie da przepołowić jedną prostą (tzn. wszystkich trzech). Naśladując zaś inne rozumowania, wykaż, że dla trzech obszarów istnieje zawsze okrąg połowiący je wszystkie (4).
"Rozmnażając" kulę
Najbardziej niesamowitym podziałem na "dwie równe części" jest tzw. paradoksalny rozkład kuli. Mianowicie w 1924 r. Stefan Banach i Alfred Tarski odkryli coś, czego na pierwszy rzut oka zrozumieć się nie da. Otóż zwykłą kulę w przestrzeni trójwymiarowej da się podzielić na takie dwie części, z których można złożyć… dwie takie same kule.
Czytelników, którzy biegną do banku, by kupić trochę złota, przerobić na kulę i podwoić swój majątek (a potem podwajać go co chwilę), oblewam zimną wodą. Zatrzymajcie się! Napisałem, że to jest "zwykła" kula. No tak, ale chodzi o kulę matematyczną, a nie fizyczną. Po drugie, podział, owszem, istnieje - ale urzeczywistnić się nie da. To też może być zresztą zagadką: istnieje - ale nie da się wykonać.
Całe rozumowanie najeżone jest trudnościami matematycznymi, jednak da się zupełnie jasno opisać równie zdumiewającą konstrukcję. Mianowicie: rozważmy linię prostą, a na niej odcinek. Możemy podzielić ten odcinek na takie rozłączne części (to znaczy niemające punktów wspólnych), że przesuwając je, jesteśmy w stanie pokryć całą prostą. Elementarna intuicja mówi nam, że to niemożliwe: odcinek ma pewną długość, powiedzmy a, zatem jego częściami nie można pokryć więcej niż a. Odcinka o długości a + 1 już nakryć się nie da.
A jednak… Ale o tym w kolejnym artykule.