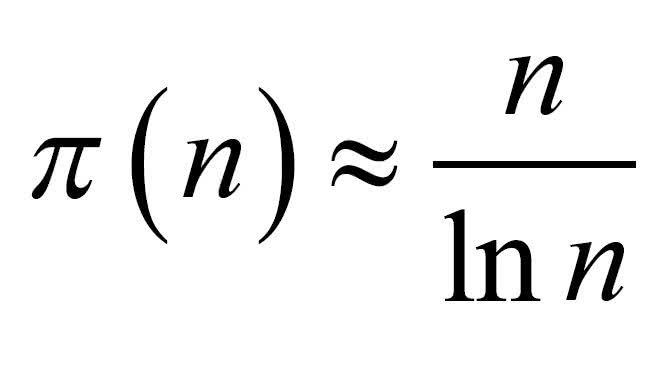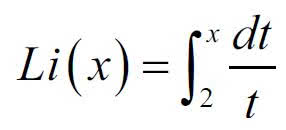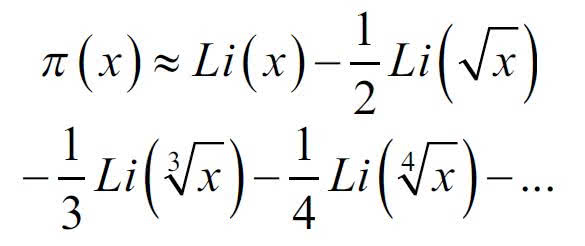Dyskretny urok liczb pierwszych

W samym słowie "liczba" mamy odniesienie do "twarzy" (a więc i do tworzenia). Twarz to "lico", obliczyć to "pokazać twarz", a więc wyjaśnić. Na poparcie tej mojej prywatnej tezy lingwistycznej mam znaczenia kilku słów w językach byłej Jugosławii (czyli państwa południowych Słowian). Ličiti znaczy "uzupełnić" po serbsku i słoweńsku, a биди сличен to po macedońsku "być podobnym". Ale i po niemiecku Zahl to liczba, zählen to "liczyć", a erzählen - opowiadać.

Policzyć komary

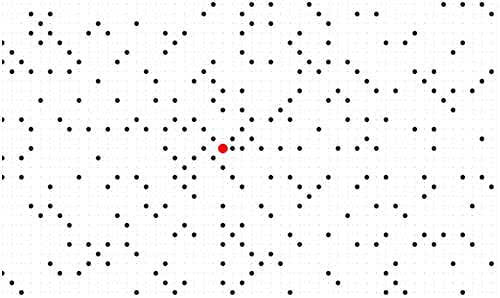
Co mają wspólnego zbiory na rys. 1 i 2?

Na rys. 1 widzimy losowo wybrane 44 punkty płaszczyzny. Tworzą one zbiór. Na rys. 2 mamy inny zbiór o tej samej liczbie elementów - czterdzieści cztery kwadraciki.

Na meczach piłkarskich większej rangi drużyny wychodzą boisko… z dziećmi. Każdy zawodnik prowadzi za rękę chłopca albo dziewczynkę. To dla zmniejszenia napięcia, złagodzenia ataku testosteronu. Potem dzieci będą pamiętać przez lata ten występ. Ile dzieci potrzeba na półfinał mistrzostw świata? Czytelnicy, którzy znają się na piłce nożnej, już znają odpowiedź: 44.

1. "A imię jego czterdzieści i cztery"

Ale dlaczego o tym piszę? Na tym przykładzie można zrozumieć odpowiedź, jaką moglibyśmy dać matematykom jeszcze XVIII wieku: co to jest liczba? Sama liczba, jako taka.

Obecnie w podstawach matematyki mówimy mniej więcej tak: liczba to jest to, co jest wspólnego w zbiorach równolicznych. Nie chcę wchodzić w te zagadnienia, zwrócę tylko uwagę, że w określeniu zbiorów równolicznych nie musimy odwoływać się do pojęcia liczby. Jeśli chcemy wiedzieć, czy w stadzie Antka jest tyle samo owiec, co w stadzie Bartka, przepuszczamy po dwie owieczki: lewą bramką owce A, prawą owce B i przy końcu widzimy już, kto miał więcej - Antek czy Bartek.

Liczby, liczby. Świat się coraz bardziej digitalizuje. Jest ich nieskończenie wiele. Umysł nasz buntuje się przed nieskończonością. Komputery jej nigdy nie ogarną. Ale czy łatwiej sobie wyobrazić, że wszystkich liczb jest tylko skończenie wiele? Dodajmy jedynkę do największej i co?… Możemy się uspokoić, przypominając sobie komary na Mazurach. Po każdym zawsze nadlatuje następny. Filozofowie nazywają to nieskończonością potencjalną: nie chodzi o nieskończony zapas, tylko o nieprzerwane stawanie się.

2. Szachownica

Metafizyka trzech typów

Takie myśli przychodzą do głowy każdemu, kto wszedł głębiej w badanie liczb pierwszych. Nie sposób odegnać metafizycznego wrażenia: jak misternie Pan Bóg stworzył naszą matematykę! Wersja dla ateistów: jak misternie skonstruowany jest ludzki umysł! Bo przecież liczby są wytworem naszego umysłu. We Wszechświecie znajdują się miliony galaktyk, ale liczby "milion" nie ma.

Liczby naturalne dzielą się na trzy typy.

Pierwszy to… liczby pierwsze.
Nazywamy tak liczby, które nie dzielą się przez nic, przez co… dzielić się muszą przez 1 i przez samą siebie. Zauważmy od razu, że terminologia polska (a także angielska, niemiecka i francuska) nie jest najszczęśliwsza. Lepsze wydaje się określenie rosyjskie: liczby proste (prostyje czisła). Ale można też uważać, że "pierwsze" znaczy "pierwotne". Z nich wszystko się składa.

Liczby, które nie są pierwsze, są złożone. Można je rozkładać na dwa lub więcej czynników pierwszych.

Uważny Czytelnik spostrzegł, że "coś tu nie gra" - gdzie jest trzeci typ? Przecież liczba albo daje się rozłożyć na więcej niż dwa czynniki pierwsze, albo nie. No tak, ale liczby 1 nie zaliczamy ani do pierwszych, ani do złożonych. Są powody logiczne, dla których musimy tak postąpić, ale nie będę się w to zagłębiał.

Liczba 2 jest pierwsza, a wszystkie pozostałe liczby pierwsze są nieparzyste. Nietrudno zauważyć, że im bardziej posuwamy się po osi liczbowej, tym rzadziej spotykamy liczbę pierwszą. Można temu nadać formę twierdzenia: najbardziej prawdopodobna różnica między kolejnymi liczbami pierwszymi dąży do nieskończoności.

W tytule artykułu jest słowo "dyskretny". W matematyce słowo to ma konkretne znaczenie. Jest przeciwstawieniem ciągłości. Dyskretny to mniej więcej to samo co "skokowy". Przepływ wody jest ciągły, upływ czasu może być skokowy - na zawodach sportowych mierzymy go na ogół z dokładnością do sekundy (kolarstwo szosowe), setnej sekundy, albo nawet tysięcznej (saneczkarstwo).

Określenie "liczby pierwsze są położone coraz rzadziej" należy rozumieć odpowiednio, bo mogą się zdarzyć nawet dwie olbrzymie liczby różniące się tylko o 2. Nazywamy je bliźniaczymi. Wypiszmy kilka takich par:

3 i 5, 5 i 7, 17 i 19, 29 i 31, 41 i 43, …, 197 i 199, …, 1639494·2⁴⁴²³-1, 1639494·2⁴⁴²³+1 , ….

Nie wiemy, czy liczb takich jest skończenie, czy nieskończenie wiele. Dokładnie sto lat temu (1919) Norweg Viggo Brun (1885-1978) wykazał, że jeżeli jest ich nieskończenie wiele, to są położone… bardzo rzadko. Matematycznie ujmuje się to tak: szereg odwrotności takich liczb jest zbieżny. To zaś z kolei znaczy, że suma 

¹/₃ + ¹/₅ + ¹/₇ + ¹/₁₁ + ¹/₁₃ + ¹/₁₇ + ¹/₁₉ + ¹/₂₉ + ¹/₃₁ + ¹/₄₁ + ¹/₄₃ + ⋯

nie przekroczy nigdy pewnej stałej, znanej właśnie jako stała Bruna. Stałą Bruna γ znamy dziś z dokładnością do 13 cyfr znaczących:

γ = 1,902160583104 …

A pouczającą ciekawostką jest to, że w 1996 r. matematyk o przyjemnym nazwisku Nicely wykazał, iż procesor Intel Pentium TM działa wadliwie, bo źle obliczał właśnie stałą Bruna. Matematyka jest wszędzie, a historia matematyki zapamięta Bruna jako autora jednego, ale głębokiego twierdzenia.

3. Liczby pierwsze lubią przekątne

Gdy pisałem swoją pierwszą książkę (1975), największymi znanymi liczbami bliźniaczymi były te ostatnie w ciągu, który napisałem wyżej. Każda z nich ma 1338 cyfr. Dzisiaj mój domowy laptop wyliczył to w ułamku sekundy, a w sierpniu 2019 r. największymi znanymi liczbami bliźniaczymi były

29966863034895·2^1290000 ±1 ,

mające po 388342 cyfry. Z pewnością rekord ten będzie szybko pobity.

Z postępów w badaniu liczb bliźniaczych wymienię dwa wyniki: istnieje nieskończenie wiele liczb pierwszych p takich, że p+2 jest albo pierwsza, albo jest iloczynem dwóch liczb pierwszych (Chen Jingrun, 1966). Drugi, nowszy wynik (2009): istnieje nieskończenie wiele par liczb pierwszych, różniących się co najwyżej o 6. Jest on o tyle interesujący, że został otrzymany przez tzw. grupę Polymath - sieć połączonych zwykłych (no, prawie zwykłych) komputerów osobistych. To jest dopiero niewiarygodne: podłączam swój komputer do sieci i mam świadomość, że jestem jednym z trybików napędzających całą machinę. Jestem małym człowieczkiem z tysiąca pchających pociąg pospieszny.

Pozostawię jako łatwe zadanie dla Czytelnika, dlaczego nie ma liczb pierwszych postaci p, p + 2, p + 4, p + 6, ale ciąg p, p + 2, p + 6, p + 8 jest już dopuszczalny? Najmniejszymi "czworaczkami" są 5, 7, 11, 13. Siódme dziesięciolecie dziewiętnastego wieku widziało takie liczby: 1871, 1873, 1877, 1879, a wielu Czytelników dożyje do 2081 r., którego młodsi bracia - 2083, 2087 i 2089 - też będą liczbami pierwszymi.

Nietrudno jest podać przykład dowolnie długiego ciągu kolejnych złożonych. Jeżeli chcę mieć, powiedzmy, 19 kolejnych liczb, wśród których nie ma ani jednej pierwszej, biorę 20! + 2, 20! + 3, 20! + 4, …, aż do 20! + 20. Pierwsza z nich jest podzielna przez 2, druga przez 3, trzecia przez 4, ostatnia przez 20. Zresztą, dalsze dwie też są złożone, a następna, czyli

20! + 23 = 2432902008176640023 ,

posłuży mi do wytłumaczenia Czytelnikowi idei "szyfrów publicznych" - szyfrów, w których co prawda podaję jawnie, jak szyfrować… ale nie wynika z tego, że umiemy złamać kod! Otóż mój laptop informuje mnie, że liczba ta nie jest pierwsza (a zatem jest złożona), ale rozłożyć jej na czynniki nie potrafi. Za trudne. Właśnie to zjawisko, że rozkładanie liczb na czynniki jest trudne obliczeniowo, stanowi podstawę tworzenia takich szyfrów. Przypomina to… chowanie liścia w lesie. Rzecz jasna, bardziej sprawny komputer rozłoży tę liczbę na czynniki, ale… po to poszukujemy dużych liczb pierwszych, żeby żaden istniejący komputer nie dał sobie rady z rozłożeniem ich iloczynu na czynniki.

Stanisław Ulam (1909-1984) był wybitnym przedstawicielem lwowskiej szkoły matematycznej. Udało mu się wyjechać z Polski na stypendium amerykańskie w 1938 r. i dzięki temu przeżył wojnę. Jest pamiętany również jako "ojciec amerykańskiej bomby wodorowej"… Niektórzy bardzo mu wypominali, że przyłożył się do wynalazku, z którego cieszyć się może tylko diabeł. Ale nie o tym chcę pisać. Podobno na jakiejś konferencji Ulam w 1963 r. strasznie się nudził. Zaczął wypisywać liczby w spirali - ot tak, zaznaczając, które są liczbami pierwszymi. Na rys. 3 mamy tę spiralę o początku 41. Ulam zauważył, że liczby pierwsze mają tendencję do układania się po przekątnych. 

Teraz proponuję trzy ciekawostki.

1. Są liczby pierwsze złożone z samych jedynek - np. 23-cyfrowa 11111111111111111111111, a są i zbudowane z kolejnych cyfr: 23, 67, 89, 4567, 56789, 456789, 23456789, 1234567891, 1234567891234567891234567891.

2. Każdy matematyk pozna od razu, co to za liczba: 31415926535897932384626433832795028841
Oczywiście - początek rozwinięcia liczby π do 38 cyfr znaczących. Jest to liczba pierwsza!

3. Co jest ciekawego w liczbie pierwszej 73939133?
To, że liczby otrzymane przez kolejne "obcinanie" jej od prawej też są pierwsze: 7393913, 739391, 73939, 7393, 739, 73, 7. Nie jest bardzo trudnym zadaniem wyliczenie wszystkich liczb mających tę własność. Są to:

53, 317, 599, 797, 2393, 3793, 3797, 7331, 23333, 23339, 31193, 31379, 37397, 73331, 373393, 593993, 719333, 739397, 739399, 2399333, 7393931, 7393933, 29399339, 29399999, 37337999, 59393339, 73939133.

Podkreślone są liczby bliźniacze. Dlaczego w całym tym ciągu nie ma cyfry parzystej?

4. Spirala Ulama. Kropkami zaznaczone są liczby pierwsze. Tu także widać, że "lubią" one ukośne rzędy (źródło rysunku: http://bit.ly/2zrFnF1)

Liczby na dywanik

W 2006 r. Chińczyk Terence Tao otrzymał Medal Fieldsa, traktowany przez matematyków jako odpowiednik nagrody Nobla - w każdym razie jeśli chodzi o prestiż, bo do nagrody dołączany jest czek na 15 tys. dolarów kanadyjskich (= cena popularnego małego samochodu, albo pensja darmozjadów z europarlamentu w Brukseli). Jednym z osiągnięć, które wyniosły go tak wysoko, był dowód (wspólna praca z Benem Greenem, 2004), że istnieją dowolnie długie ciągi arytmetyczne złożone z liczb pierwszych. Trudno w tym artykule przekazać doniosłość takiego osiągnięcia. Ma jednak ono trochę "polskich korzeni": rozważania na ten temat pojawiały się w pracach młodych polskich matematyków lat 50. i 60. XX wieku. Wymienię tu tylko nazwisko Andrzeja Mąkowskiego.

Wiek XIX przekazał nam idylliczny obraz nauki: bezinteresownej walki o poznanie. Jeden z najwybitniejszych polskich matematyków, którego inicjały zaszyfruję pod X.Y., miał zasadę: profesor może mieć tylko jednego ucznia. Spośród kilku młodych zdolnych adeptów wybrał jednego - resztę odrzucił. Andrzej Mąkowski był jednym z odrzuconych. Innym był J.B. (inicjały zmyślone). Gdy w 2005 r. J.B. otrzymał nagrodę imienia X.Y., napisał w sposób obraźliwy dla Jury, że jej nie przyjmuje. Natomiast zmarły w 1999 r. Mąkowski nie wyszedł poza magisterium - ale jego zasługi dla matematyki polskiej są na pewno większe niż profesora X.Y. To wyleczyło mnie z idyllicznego obrazu nauki. Nie o tym jednak ten artykuł.

Mamy w języku potocznym zwrot "rozłożyć na czynniki pierwsze". Rozumiemy - to taki rozkład, że dalej już nie można. Gdzie jest dodawanie i mnożenie, tam możemy rozkładać wyrażenia na iloczyn. Pamiętamy ze szkoły: a² - b² = (a + b)(a - b).

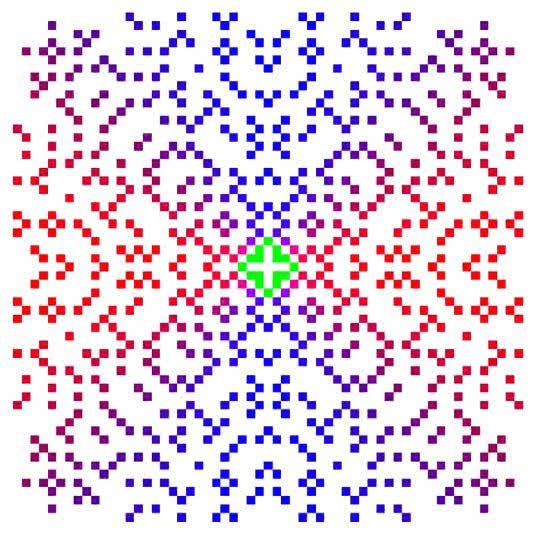
Większość Czytelników zna liczby zespolone. To liczby postaci a + bi, gdzie i² = -1 . Działania na nich podlegają takim samym prawom, jak na zwykłych liczbach (zwanych w szkole liczbami rzeczywistymi). Na przykład (1 + 2i)(1 + i) = -1 + 3i, a zatem -1 + 3i rozkłada się na iloczyn dwóch czynników. Nie jest zatem liczbą pierwszą. Te, które są pierwsze, nazywają się liczbami pierwszymi Gaussa. Wystarczy spojrzeć na rys. 5, żeby… je polubić. Otrzymałem kiedyś w prezencie od pewnej pani z Gdańska dywanik z wyhaftowanymi (haftem krzyżykowym) liczbami pierwszymi Gaussa. Jest piękny.

5. Liczby pierwsze Gaussa

Zanim jeszcze liczby pierwsze znalazły nieoczekiwane zastosowanie w kryptografii (a to obejmuje nie tylko kody dostępu do urządzeń mogących zniszczyć świat, ale i np. podpis elektroniczny), były przedmiotem badań generacji matematyków. Zadziwili się nimi już starożytni Grecy. Prosty dla dzisiejszego ucznia dowód, że liczb pierwszych jest nieskończenie wiele, wywoływał dreszczyk metafizycznej emocji wśród pokoleń filozofów - głównie przez użycie metody "nie wprost". Sherlock Holmes mawiał, że jeżeli wyeliminujemy to, co niemożliwe, to to, co zostaje, choćby nieprawdopodobne, jest prawdziwe. Tak sformułowana zasada logiczna nie jest oczywiście prawdziwa (Czytelniku: dlaczego?), ale nietrudno ją sformułować poprawnie. Jest to jeden z tzw. kanonów logicznych Johna Stuarta Milla.

6. Przyrost liczb pierwszych

Co by było, gdyby liczb pierwszych było tylko skończenie wiele? Można by je wszystkie pomnożyć; wyszła by może olbrzymia, ale przecież jakaś liczba, niech będzie N. Dodajmy do niej 1. Nowa liczba, N + 1, nie dzieli się przez żadną z liczb pierwszych, bo zawsze zostaje reszta 1. Skoro tak, sama jest nową liczbą pierwszą. Czyli założyliśmy, że wypisaliśmy wszystkie liczby pierwsze, a okazuje się, że nie wszystkie! Jedynym wyjściem z tej sprzeczności jest to, że nie mogliśmy wypisać wszystkich liczb pierwszych. Jest ich zatem nieskończenie wiele. Choćbyśmy odlecieli od początkowej liczby 1 na miliony lat świetlnych, zawsze przed nami będzie jeszcze… nieskończenie wiele liczb pierwszych.

Jak pisałem, liczby pierwsze leżą coraz rzadziej, gdy posuwamy się wzdłuż osi liczbowej. Jak rzadko? Jak to zmierzyć?

Istnieje wiele wzorów przybliżonych. Najdawniejszy z nich to:

,

gdzie w mianowniku stoi logarytm naturalny liczby n, czyli logarytm o podstawie e = 2,7182… Możemy porównać te dwie funkcje - widzimy, że przybliżenie jest zawsze z niedomiarem.

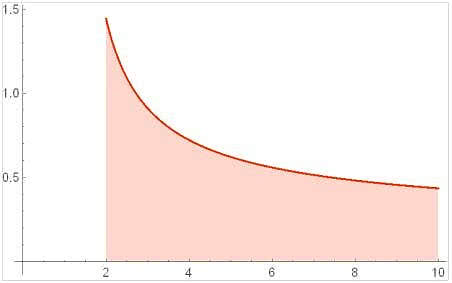
Czy można znaleźć lepsze przybliżenia? Można. Pomaga funkcja zwana logarytmem całkowym, a oznaczana przez Li. Określamy ją dla x > 2. Dla Czytelników znających rachunek całkowy podam właśnie wzór całkowy:

,

a kto tego rachunku nie zna, zrozumie takie określenie z rys. 7. Widoczna tam krzywa to odwrotność logarytmu, a wartość Li(x) to pole pod tą krzywą od 2 do x. Na rysunku x = 10. Wartość Li(10) to zaznaczone pole, równe w przybliżeniu 5,12.

7. Logarytm całkowy

Bernhard Riemann (1826-1866), słynny w matematyce z nieco innego powodu niż badanie liczb pierwszych, odkrył bardzo dokładne przybliżenie funkcji ?(?). Wzór jest skomplikowany, ale bardzo ładny. Doprawdy, nawet matematyk zastanawia się "jak on na to wpadł":

Przybliżenie to jest już bardzo dobre. Jeżeli oznaczymy funkcję po prawej stronie przez R(x), to mamy np. π(1000000000) = 50847534 , a R(1000000000) = 50847455; błąd bardzo, bardzo mały. Naprawdę, to zdumiewające.Riemann poszedł dalej i odkrył dokładny wzór na π(x).

Wprowadził do gry pewną funkcję dwóch zmiennych i oznaczył ją grecką literą ζ (dzeta). Wykazał, że π(x) = R(x) minus suma wartości R(x^p) we wszystkich miejscach zerowych p funkcji dzeta. Uff, trudne. Ale czy to znaczy, że wiemy już wszystko? I tak, i nie. Nie umiemy znaleźć wszystkich miejsc zerowych funkcji dzeta. Hipotezą samego Riemanna było podejrzenie, że leżą one wszystkie na jednej prostej. Ale ani jej udowodnić, ani ją obalić - tego na razie nikt nie potrafi. Co więcej, to obecnie najpoważniejszy problem matematyczny do rozwiązania. Niektórzy wieszczą kasandrycznie, że po udowodnieniu tej hipotezy będziemy mogli stworzyć sztuczną inteligencję, po czym nastąpi koniec świata. Czytelniku - maturzysto, sprawdź, czy rozumiesz zwrot "kasandryczna przepowiednia"…

Ale dlaczego to takie ważne? Nie chodzi tylko o sprawy "metafizyczne" - zyskujemy dokładną wiedzę o liczbach pierwszych. Po prostu - kto lepiej zna liczby pierwsze, może konstruować lepsze szyfry. Trochę szkoda, że tak się stało, iż liczby pierwsze nie pozostały w trudno dostępnym "mateczniku matematyki".

Głupi niedźwiedziu - gdybyś w mateczniku siedział, Nigdy by się o tobie Wojski nie dowiedział!
(zapomniany poeta XIX wieku, pan Tadeusz, w poemacie "Adam Mickiewicz")