Prosto, w lewo, w prawo

Uczniowie nie wiedzieli, co to znaczy "zapisać coś w kominie". Nie wiedzieli też, co ma z tym wspólnego Pitagoras. W twierdzeniu Pitagorasa jest przecież mowa o trójkątach. Wyjaśniłem, że rola Pitagorasa w kulturze europejskiej polega na tym, że założył on pierwszą "szkołę". Piszę w cudzysłowie, bo było to coś pośredniego między szkołą w dzisiejszym sensie, klasztorem, sektą i towarzystwem naukowym.
"Przeznaczeniem człowieka jest badać świat" - tak można streścić przesłanie, które zostawił on pokoleniom Europejczyków. Zostawił ciekawość świata, narzucił badania, które można by nazwać naukowymi. Refleksja nad własnym rozumem, nad nieograniczonością świata, nad prostymi regułami geometrii, z których wynikają prawa świata. Dlatego właśnie Jerzy Harasymowicz wplótł Pitagorasa do swojego wiersza.
Trudno zrozumieć, dlaczego linia prosta jest zmęczona i chce się zwinąć w kłębek. Może to nic nie znaczy, a może poeta antycypował tzw. twierdzenie Borsuka?
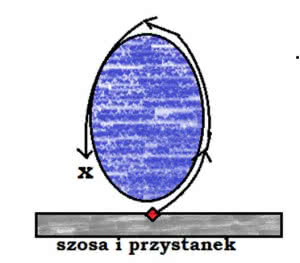
Karol Borsuk (1905-1982) był wybitnym matematykiem, związanym z Warszawą. Jednym z ostatnich jego odkryć matematycznych jest twierdzenie o zanurzaniu. Każda przestrzeń wymiaru n da się zanurzyć w małą kulkę w przestrzeni o wymiarze n+1. Rysunek 1 pokazuje, co zrobić z linią prostą.
Z kolei Julian Tuwim sam się przyznawał do tępoty do matematyki. Trudno w to uwierzyć, ale taka kokieteryjna postawa przydawała się dawniej tak, jak i teraz ("nie umie nic - to swój chłop!").
Jednak za czasów Tuwima, w carskiej szkole, matematyka sprowadzała się do nudnych rachunków, w tym algebraicznych i trudnej geometrii. W cytowanym wierszu poeta określił swoje stanowisko w średniowiecznym sporze o uniwersalia. O co w tym sporze chodziło? Czy obiekty badań matematycznych istnieją w przyrodzie? A może nie istnieją w przyrodzie, tylko…, no właśnie, gdzie? W umysłach ludzi? To gdyby nie było ludzi, to linii prostych by nie było? A gdy ludzkość wyginie, to czy 7 będzie nadal liczbą pierwszą?
Czytelnik, który żachnie się: a po co nad czymś takim się zastanawiać - będzie miał dużo racji. Przynajmniej w dzisiejszym, zracjonalizowanym świecie. Podczas wspomnianych warsztatów przeszliśmy zatem do dyskusji o lewej i prawej stronie.
Prawy do lewego, czyli gdzie?
Temat ten frapuje mnie od momentu, kiedy (wiele lat temu) moja znajoma powiedziała mi, że po wyjściu z autobusu mam jej szukać po prawej stronie podługowatego jeziora. Konkretnie, chodziło o małe jezioro Giby na Suwalszczyźnie.
Poszedłem tak, jak na schematycznym rysunku 2. Obszedłem jezioro dookoła i znalazłem obóz harcerski (na którym znajoma była wychowawczynią), ale dopiero w miejscu zaznaczonym krzyżykiem. Na moje zdziwienie odpowiedziała własnym:
- Przecież mówiłam, że po prawej stronie jeziora - to znaczy, że jezioro będziesz miał po prawej!
Geometria różni się od arytmetyki znacznym udziałem intuicji. Nic dziwnego - wyobrażenia przestrzenne tworzą się w nas od pierwszych dni życia, a podstawą wszelkich wyobrażeń są pojęcia "wewnątrz" i "na zewnątrz".
Stąd wyrasta pojęcie odległości, które zostaje pogłębione, gdy dziecko własnymi krokami zaczyna przemierzać przestrzeń. Stopniowo opanowuje ono (a prawie każdy z nas był dzieckiem, jak stwierdził w przedwojennym polskim filmie "Zapomniana melodia" Antoni Fertner) kolejne pojęcia geometryczne: przed-za, pod-nad, od-do, stąd-dotąd, tędy, przez, obok, między, na górze - na dole, pod spodem - na wierzchu, z przodu - z tyłu, i wreszcie najtrudniejsze: lewo-prawo. Jak wspomniałem, przekonały się o tym moje nogi. Jest to często związane z ruchem.
Gdy na pytanie, gdzie mam zatrzymać samochód, usłyszę od żony "za tym czerwonym bububu" (nie rozumiejąc ostatniego słowa), to jeżeli "bububu" oznacza inny samochód parkujący na mojej uliczce, wówczas nie wyprzedzę go, ale stanę tak, jak za kimś w kolejce. Jeśli jednak będzie to znaczyło "za tym czerwonym domem", zachowam się przeciwnie: minę ten dom, by stanąć za nim - mieć go z tyłu.
Wyjeżdżając samochodem z podporządkowanej ulicy i skręcając w prawo, włączam prawy kierunkowskaz. Ale gdy ta ulica wpada do głównej łagodnie, pod niewielkim kątem - mam już wątpliwości: lewy czy prawy.
Gdy wjeżdżam zaś z prawego pasa na lewy, włączam oczywiście lewy. A przecież dla pojazdów mających pierwszeństwo wjeżdżam na ich pas z prawej. Zauważmy tu, że choć lusterko samochodowe (jak każde inne) odwraca lewo i prawo, to migający kierunkowskaz samochodu jadącego za mną i chcącego skręcić w lewo, zobaczę po lewej stronie!
Jeżeli płynę na plecach blisko liny oddzielającej tory na basenie i mam linę po lewej ręce, to właśnie płynę prawą stroną.
Strzałka skierowana do góry na napis "Gdańsk" i strzałka skierowana do dołu na napis "Gdańsk" nad naszym pasem ruchu na autostradzie upewni nas w tym samym: jedziemy do Gdańska.
Czy zastanawiałeś się, Czytelniku, dlaczego lustro, do którego zerkasz przy goleniu/makijażu, odwraca lewo i prawo, a nie odwraca góry i dołu?
Gdy flisak na Dunajcu powie, że niebezpieczne skały ominiemy z prawej, wiemy, że zostawimy je po lewej. Jeżeli jednak powie, że "z lewej mijamy Trzy Korony", spojrzymy też ku lewemu brzegowi. Trudne i nielogiczne, prawda? Nic dziwnego: nie osiągnie wyżyn ten, kto miał "do szkoły pod górkę".
Większość ludzi jest praworęczna, ale "tylko" większość. Jeszcze za mojego dzieciństwa przymuszano dzieci do pisania zawsze prawą ręką. W każdym języku "prawo" kojarzy się z porządkiem i dobrem.
Na uniwersytetach są wydziały prawa. Mamy zaś "lewe" interesy, "lewe" dochody. Unikaj szefa, jeżeli wstał dziś lewą nogą i włożył koszulę na lewą stronę. Coś niedobre jest "do luftu" i nie ma to związku z niemieckim das Luft - powietrze, tylko z angielskim left albo lyft, stąd niemieckie links (lewo).
Jedyne dobre skojarzenie, jakie mi przychodzi ze słowem "lewy", to Robert Lewandowski, nazywany podobno "Levy". O polityce (partie lewicowe i prawicowe) dyskutować tu nie będziemy.
Uff. Wiemy, że nie jesteśmy całkiem symetrycznie zbudowani. Nie chodzi o organy wewnętrzne, ale o sam wygląd. Na ogół mamy silniejszą prawą stronę, ale bywa inaczej. I oto pouczające zadanie.
Zadanie 1. Lewą nogą stawiam krok dłuższy o 0,1 cm niż prawą. Jak będzie wyglądać moja droga na dużym placu, w gęstej mgle, to znaczy przy braku możliwości korekty wzrokowej?
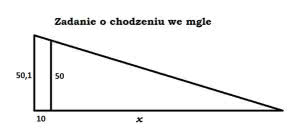
Rozwiązanie jest proste. Spójrzmy na rysunek 3. Gdy nie mamy możliwości korygowania kierunku marszu wzrokiem (np. mgła na pustej przestrzeni), to po każdym kroku mimowolnie skręcamy. Załóżmy, że stawiamy kroki półmetrowe, a odległość między stopami to 10 cm. Układamy proporcję: x/50=(x+10)/50,1.
Każdy rozwiąże. Wynik zaskakuje: x=5000 cm, a więc 50 m. Wystarczy więc 1 mm różnicy w długości kroku, a będziemy zataczać koła o średnicy 100 m i "nigdy" nie wydostaniemy się z tego zaklętego kręgu! Przerażające, prawda? Opowieści podróżnicze są pełne historii o wędrowcach natrafiających co pewien czas na swoje własne ślady.
Ciekawa, ale krótka była podczas warsztatów dyskusja na temat ruchu lewo- i prawostronnego. Jak zaplanować operację przejścia na "ten przeciwny"? Nie jest to tylko zagadnienie teoretyczne. W 2009 r. na ruch lewostronny (tak, z prawego na lewy) weszło państwo Samoa. Ale nie jest to temat do kącika matematycznego.
"Lewo i prawo" to wstęp do "symetrii". Wiele zadań geometrycznych rozwiązuje się, używając symetrii.
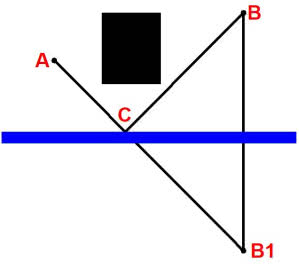
Najbardziej znane jest następujące. Chcę dojechać konno z punktu A do punktu B (jak na rysunku 4) tak, żeby droga była jak najkrótsza, a koń napił się wody z rzeki. Zadanie o tej samej treści matematycznej: z punktu A chcę oświetlić punkt B, ale między nimi jest przeszkoda. Na szczęście mam lustro…
W obu przypadkach rozwiązanie jest takie same: odbijam punkt B symetrycznie względem prostej, łączę A linią prostą z B1 i wyznaczam punkt C. Jest on miejscem, w którym koń napije się wody, albo punktem, na który skieruję promień światła z A, żeby dotarł do B.
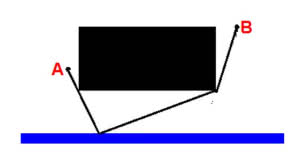
Sytuacja komplikuje się, gdy przeszkoda między punktami jest duża (5).
Pomysł "odbijmy symetrycznie, a wszystko się uprości" wykorzystujemy w wielu zadaniach geometrycznych. Tutaj tylko jedno.
Zadanie 2. Na bokach trójkąta obieramy punkty P, Q, R, po jednym na każdym boku. Jak to zrobić, by trójkąt PQR miał jak najmniejszy obwód?
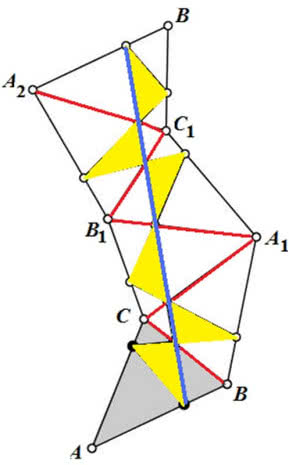
Rozwiązaniem jest tzw. trójkąt ortyczny, czyli taki, że punkty P, Q, R są spodkami trzech wysokości trójkąta. Pomysłowy dowód widzimy na rysunku 6. Odbijamy trójkąt kilkakrotnie. Z trójkąta ortycznego powstaje linia prosta (poprawniej: odcinek) - a to jest najkrótsza droga między dwoma punktami.
Po schodach Julii do spiral Archimedesa
Uczestnikami zajęć, o których tu piszę, byli uczniowie (16 chłopców i jedna Julia) z 7-8 klas szkół podstawowych. Takich dzieci nie należy zanudzać zbyt górnolotną matematyką. Swoją drogą, kogo można wobec tego zanudzać? Pozostawię to pytanie bez odpowiedzi. Moim podopiecznym dałem zadanie o schodach. Nie wszyscy wiedzieli, dlaczego w zamkach średniowiecznych schody były prawie zawsze lewoskrętne. Na takich schodach ludziom praworęcznym łatwiej się bronić przed atakującymi z dołu.
Na zajęciach należało z klocków Lego zbudować na niewielkiej podstawce stabilne schody lewo- i prawoskrętne. Dyskusję wywołało pojęcie stabilności schodów.
Pamiętam, jak na drugim roku studiów "obliczaliśmy schody" - ich wytrzymałość. Są na to gotowe wzory, ale chcieliśmy je sprawdzić matematycznie. Na naszych warsztatowych zajęciach najlepsze schody wykonała Julia - zadbała o stabilność i estetyczny dobór kolorów (7). Chłopcy robili byle jak i pstrokato.
Pytanie matematyczne związane ze schodami wydaje się oczywiste: ile klocków potrzeba na zbudowanie schodów aż do n-tego piętra? Odpowiedź jest dość prosta - obliczajmy wysokości kolejnych słupków. Mamy sumy kolejnych liczb 1+2+3+ i tak dalej.
Jeżeli wykorzystamy podstawkę taką, jaką wzięła Julia, to możemy ułożyć schody aż do jedenastego piętra. Sumę kolejnych liczb od 1 do 11 obliczyć nietrudno, a "sprytny" sposób to taki: pod sumą piszemy drugą taką samą, tylko w odwrotnej kolejności:
1+2+3+4+5+6+7+8+9+10+11+
11+10+9+8+7+6+5+4+3+2+1.
Tworzy się jedenaście słupków
(1+11=2+10=3+9 itd.) o sumie 12. Trzeba tylko pomnożyć 11 przez 12, żeby dostać podwojoną sumę, którą obliczamy. Wynikiem jest 66.
Matematycznie najciekawszym zadaniem okazało się budowanie z klocków spirali Archimedesa. Na rysunkach 8 i 9 mamy spirale lewoskrętne - "prawdziwą", czyli taką jak zwoje na płycie gramofonowej, oraz ułożoną z prostokątnych klocków.
Oczywiście teoretycznie obie spirale rozwijają się do nieskończoności. Widać, co jest charakterystycznego w spirali Archimedesa - jednakowa odległość kolejnych zwojów. Dlatego taka spirala nadaje się do płyt z muzyką - oczywiście płyt winylowych, które wracają do użytku.
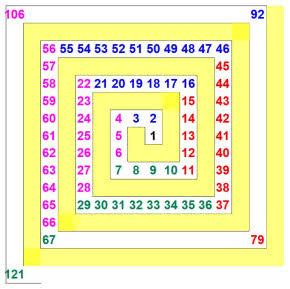
Zadanie 3. Ułóż lewoskrętną i prawoskrętną "kwadratową" spiralę. Zacznij tak, jak na rysunku 9. Kolory powtarzają się wg widocznego wzoru. Jaki jest kolor zwoju nr 2020? Jakich kolorów są kwadraty narożne? Odkryj regułę. Ile klocków jest potrzebnych do spirali z n zwojami?
Numerujemy kolejne klocki w spirali. Czarny kwadrat ma numer 1, potem są niebieskie 2, 3, żółte 4, 5, 6 i tak dalej (10).
Jakiego koloru jest klocek o numerze 2020? A klocek o numerze 10 000?
Ile klocków poszczególnych kolorów potrzebnych jest do spirali o stu zwojach? Odkryj też ogólną regułę (tzn. dla spirali o n zwojach).
Zwróć uwagę, że białe pola na tym rysunku też tworzą spiralę. Czy jest ona lewo- czy prawoskrętna? Ułóż samodzielnie INNE ZADANIA o spirali. Rozwiąż je.
Na rozwiązanie tych zadań zabrakło nam czasu na zajęciach… i miejsca w tym artykule.
Michał Szurek