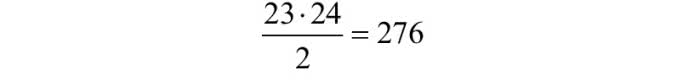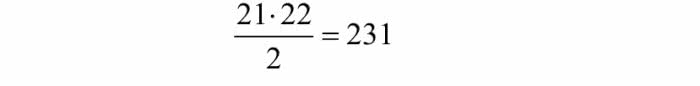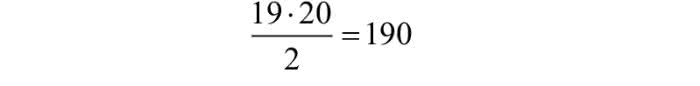Szyfry i szpiedzy

W szkole mówi się coraz więcej o "kodowaniu", rozumiejąc przez to czynność zwaną dawniej "programowaniem". To częsty zabieg dydaktyków-teoretyków. Odkopują stare metody, nadają im nową nazwę i "postęp" robi się sam. Mało jest dziedzin, w których zachodzi tak cykliczne zjawisko.

Można by wywnioskować, że deprecjonuję dydaktykę. Nie. W rozwoju cywilizacyjnym wracamy niekiedy do tego, co było, zostało zarzucone, a teraz odżywa. Ale nasz kącik jest matematyczny, a nie filozoficzny.

Przynależność do pewnej wspólnoty znaczy również "wspólne symbole", wspólne lektury, powiedzenia i przypowieści. Ktoś najlepiej nauczony języka polskiego - i mówiący bezbłędnie "w Szczebrzeszynie duży gąszcz, tam rozbrzmiewa w trzcinie chrząszcz" - zostanie natychmiast zdemaskowany jako szpieg obcego mocarstwa, gdy nie odpowie na pytanie, co robi dzięcielina. Oczywiście pała!

To nie jest tylko żart. W grudniu 1944 r. Niemcy przeprowadzili dużym kosztem ostatnią ofensywę w Ardenach. Zmobilizowali żołnierzy mówiących biegle po angielsku, żeby dezorganizowali ruchy wojsk alianckich, np. kierując je w niewłaściwym kierunku na skrzyżowaniach dróg. Po chwilowym zaskoczeniu Amerykanie zaczęli zadawać podejrzanym żołnierzom pytania, na które odpowiedzi byłyby oczywiste dla człowieka z Teksasu, Nebraski czy Georgii, a niepojęte dla kogoś, kto się tam nie wychował. Nieznajomość realiów prowadziła wprost pod pluton egzekucyjny.

Do rzeczy. Polecam Czytelnikom książkę Łukasza Badowskiego i Zasława Adamaszka "Laboratorium w szufladzie - matematyka". To piękna książka, znakomicie pokazująca, że matematyka naprawdę się do czegoś przydaje oraz że "eksperyment matematyczny" to nie puste słowa. Jest w niej m.in. opisana konstrukcja "tekturowej Enigmy" - przyrządu, do stworzenia którego potrzebujemy zaledwie piętnastu minut, a działającego jak poważna maszyna szyfrująca. Sam pomysł był jako tako znany, wspomniani autorzy ładnie go opracowali, a ja go trochę zmienię i opakuję w bardziej matematyczne szaty.

Szyfrujące trylinki

Na jednej z ulic mojego osiedla na przedmieściach Warszawy rozebrano niedawno nawierzchnię z "trylinki" - sześciokątnych płyt brukowych. Jechało się po tym niewygodnie, ale dusza matematyka radowała się. Niełatwo jest pokryć płaszczyznę regularnymi (to jest foremnymi) wielokątami. Mogą to być tylko trójkąty, kwadraty i właśnie sześciokąty foremne.

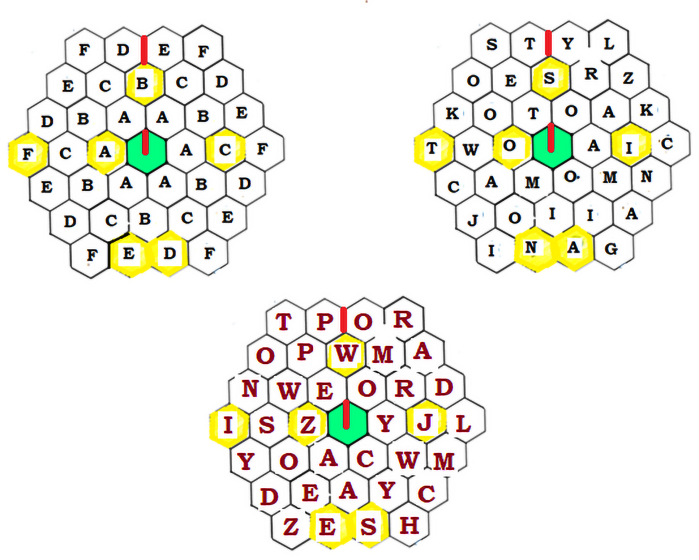
Może trochę żartuję z tą radością duszy, ale sześciokąt jest ładną figurą. Da się go wykorzystać do całkiem udanego urządzenia szyfrującego. Pomoże geometria. Sześciokąt ma symetrię obrotową - nakłada się sam na siebie po obrocie o wielokrotności kąta 60 stopni. Pole oznaczone np. A w lewej górnej części rys. 1 po obrocie o taki kąt przejdzie też na pole A - i tak samo z innymi literami. Wytnijmy zatem z siatki sześć pól, każde z inną literą. Połóżmy tak otrzymaną siatkę na kartce papieru. W wolne sześć pól wpiszmy sześć liter tekstu, który chcemy zaszyfrować. Obróćmy kartkę o 60 stopni. Ukaże się sześć nowych pól - wpisujemy w nie dalsze sześć liter naszej wiadomości.

Rys. 1. Trylinki radością matematyka.

Po prawej stronie rys. 1 mamy zaszyfrowany w ten sposób tekst: "Stoi na stacji lokomotywa ciężka ogromna i".

Teraz przydaje się trochę matematyki licealnej. Na ile sposobów można ustawić dwie liczby, jedna z drugą?

Co za niemądre pytanie? Na dwa: albo jedna z przodu, albo druga.

Bardzo dobrze. A trzy liczby?

Też nietrudno wymienić wszystkie ustawienia:

123, 132, 213, 231, 312, 321.

No, to dla czterech! Jeszcze da się to jasno napisać. Odgadnij zasadę porządku, w jakim ustawiam:

1234, 1243, 1423, 4123, 1324, 1342,

1432, 4132, 2134, 2143, 2413, 4213,

2314, 2341, 2431, 4231, 3124, 3142,

3412, 4312, 3214, 3241, 3421, 4321.

Gdy liczb będzie pięć, otrzymamy już 120 możliwych ustawień. Zwiemy je permutacjami. Liczba możliwych permutacji n liczb to iloczyn 1·2·3·…·n, nazywany silnią i oznaczany wykrzyknikiem: 3!=6, 4!=24, 5!=120. Dla następnej liczby 6, mamy 6!=720. Wykorzystamy to do skomplikowania naszej sześciokątnej tarczy szyfrującej.

Wybieramy permutację liczb od 0 do 5, np. 351042. Nasza sześciokątna tarcza szyfrująca ma kreskę w środkowym polu - po to, żeby można ją było ustawić "w położeniu zerowym" – kreską do góry, tak jak na rys. 1. Kładziemy tak tarczę na kartce, na której mamy zapisać nasz meldunek, ale nie piszemy od razu, tylko przekręcamy ją o trzy razy 60 stopni (czyli o 180 stopni) i wpisujemy sześć liter w wolne pola. Wracamy do położenia wyjściowego. Przekręcamy tarczę o pięć razy 60 stopni, czyli o pięć "ząbków" naszej tarczy. Wpisujemy. Następnym położeniem tarczy jest to, które względem zerowego jest obrócone o 60 stopni. Czwarte położenie odpowiada 0 stopni, czyli jest to położenie wyjściowe.

Czy rozumiesz, co się stało? Dostaliśmy dodatkową możliwość - skomplikowania naszej "maszyny" ponad siedemset krotnie! Mamy więc dwa niezależne położenia "maszyny" - wybór siatki i wybór permutacji. Siatkę można wybrać na 66=46656 sposobów, permutacji jest 720. Daje to 33592320 możliwości. Ponad 33 miliony szyfrów! Praktycznie trochę mniej, bo niektóre siatki nie dadzą się wyciąć z papieru.

W dolnej części rys. 1 mamy zaszyfrowany w ten sposób komunikat: "Posyłam wam cztery dywizje spadochronowe". Łatwo zrozumieć, że nie wolno dopuścić do tego, by wróg się o tym dowiedział. Ale czy zrozumie coś z tego:

TPOROPWMANWEORDISZ
YJLYOACWMDEAYCZESH,

nawet z podpisem 351042?

Budujemy Enigmę - niemiecką maszynę szyfrującą

Rys. 2. Przykładowe początkowe ustawienie naszej maszyny szyfrującej.
Permutacja (AF) (BJ)(CL)(DW)(EI)(GT) (HO)(KS)(MX)(NU) (PZ)(RY).

Jak wspomniałem, pomysł budowy takiej "maszyny" z tekturki zawdzięczam książce "Laboratorium w szufladzie - matematyka". Moja "konstrukcja" różni się trochę od podanej przez jej autorów.

Używana przez Niemców w czasie wojny maszyna szyfrująca miała genialnie prostą zasadę, nieco podobną do tej, którą widzieliśmy przy szyfrze z sześciokątem. Chodzi za każdym razem o to samo: rozbić sztywne przyporządkowanie literze innej litery. Ma to być zmienne. Jak to zrobić, żeby mieć nad tym kontrolę?

Wybierzmy nie dowolną permutację, tylko taką, która ma cykle długości 2. Mówiąc prościej, coś w rodzaju opisywanego tu kilka miesięcy temu "Gaderypoluki", tylko żeby obejmowało wszystkie litery alfabetu. Zgódźmy się na 24 litery - bez ą, ę, ć, ó, ń, ś, ó, ż, ź, v, q. Ile jest takich permutacji? To zadanie dla maturzystów (powinni to umieć rozwiązać natychmiast). Ile? Dużo? Kilka tysięcy? No, tak:

1912098225024001185793365052108800000000 (nawet nie próbujmy czytać tej liczby). Tyle jest możliwości ustawienia "zerowego" położenia. A jeszcze to można komplikować.

Nasza maszyna składa się z dwóch kolistych tarcz. Na jednej z nich, nieruchomej, są wypisane litery. Przypomina to trochę tarczę dawnego telefonu, gdzie wybierało się numer, kręcąc tarczą do oporu. Obrotowa jest druga, z naniesionym kolorowym schematem. Najprościej umieścić je na zwykłym korku, za pomocą pineski. Zamiast korka można użyć cienkiej deseczki, albo grubej tektury. Łukasz Badowski i Zasław Adamaszek w swojej książce polecają umieszczenie obu tarcz w pudełku po płytce CD.

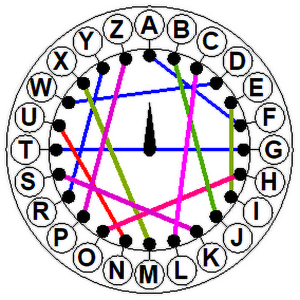
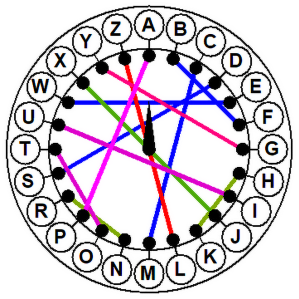
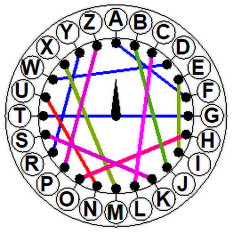
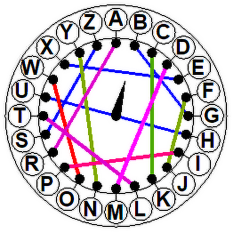
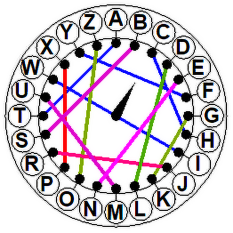
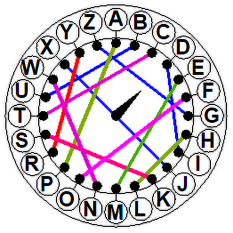
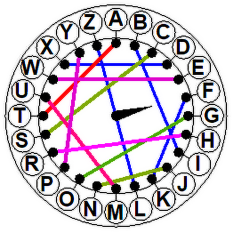
Wyobraźmy sobie, że chcemy zaszyfrować słowo ARMATY (rys. 2 i 3). Ustawiamy urządzenie w pozycji zerowej (strzałka do góry). Literze A odpowiada F. Obracamy wewnętrzną tarczkę o jedną literę w prawo. Do zaszyfrowania mamy literę R, odpowiada jej teraz A. Po kolejnym obrocie widzimy, że literze M odpowiada U. Kolejny obrót (czwarta tarczka) daje odpowiedniość A - P. Na piątej tarczy mamy T - A. Wreszcie (szóste kółko) Y - E. Wróg na pewno nie zgadnie, że nasze FAUPAE będą groźne dla niego. A jak "nasi" odczytają depeszę? Muszą mieć taką samą maszynę, "zaprogramowaną" tak samo, to znaczy z tą samą permutacją. Szyfrant zaczyna z pozycji zerowej. Zatem znaczeniem litery F jest A. Przekręca tarczę w prawo. Z literą A skojarzona jest teraz R. Przekręca tarczę w prawo i pod literą U znajduje M itd. Szyfrant biegnie do generała: "Panie generale, melduję, że idą armaty!".

Rys. 3. Zasada działania naszej papierowej Enigmy.​

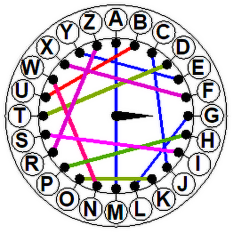Rys. 3. Zasada działania naszej papierowej Enigmy.

Możliwości nawet takiej prymitywnej Enigmy są niesamowite. Możemy wybierać inne permutacje wyjściowe. Możemy - i tu tkwi jeszcze więcej możliwości - nie obracać regularnie po jednym "ząbku", a w określonym, codziennie zmienianym porządku, podobnie jak przy sześciokącie (np. najpierw obrót o trzy litery, potem o siedem, potem o osiem, cztery… itd.).

Jak to można odgadnąć?! A jednak polskim matematykom (Marian Rejewski, Henryk Zygalski, Jerzy Różycki) się to udało. Wiadomości uzyskiwane w ten sposób były bezcenne. Równie ważny wkład w dzieje naszej obronności mieli wcześniej Wacław Sierpiński i Stanisław Mazurkiewicz, którzy w 1920 r. złamali szyfr wojsk rosyjskich. Przechwycona depesza dała Piłsudskiemu możliwość wykonania słynnego manewru znad Wieprza.

Wacława Sierpińskiego (1882-1969) pamiętam. Wydawał się matematykiem, dla którego świat zewnętrzny nie istnieje. O swoim udziale w zwycięstwie w 1920 r. mówić nie mógł i ze względów wojskowych, i… politycznych (władze PRL nie lubiły tych, co bronili nas przed Związkiem Radzieckim).

Rys. 4. Permutacja (AP)(BF)(CM)(DS)(EW)(GY)(HK)(IU) (JX)(LZ)(NR)(OT).

Rys. 5. Ładny ornament, ale do szyfrowania się nie nadaje. Zbyt regularny.

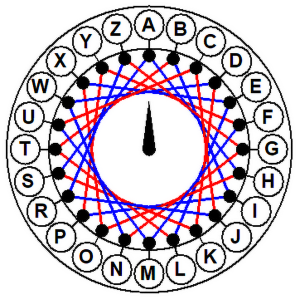
Zadanie 1. Na rys. 4 masz inną permutację, służącą do budowy Enigmy. Odbij rysunek na kserografie. Zbuduj maszynę, zakoduj własne imię i nazwisko. Moje to CWONUE JTRYGT. Jeżeli masz potrzebę utajnienia swoich notatek, użyj tekturowej Enigmy.

Zadanie 2. Zaszyfruj swoje imię i nazwisko za pomocą jednej z "maszyn", które widziałeś, ale (uwaga!) z dodatkową komplikacją: obracamy nie o jeden ząbek w prawo, ale według schematu {1, 2, 3, 2, 1, 2, 3, 2, 1, ….} - tzn. najpierw o jeden, potem o dwa, potem o trzy, następnie o 2, znów o 1, potem 2 itd., taką "falką". Sprawdź, że moje imię i nazwisko zaszyfruje się jako CZTTAK SDBITH. Czy teraz rozumiesz, jak potężną maszyną była Enigma?

Rozwiązanie zadania dla maturzystów. Ile jest możliwości ustawienia Enigmy (w tej wersji jak opisana w artykule)? Mamy 24 litery. Wybieramy pierwszą parę liter - możemy to zrobić na

sposobów. Następną parę możem y wybrać na

sposobów, następną na

itd. Po stosownych obliczeniach (wszystkie liczby należy pomnożyć) otrzymamy

151476660579404160000.

Następnie liczbę tę należy podzielić przez 12! (silnia 12), ponieważ te same pary mogą być otrzymane w różnej kolejności. Ostatecznie otrzymujemy więc "tylko"

316234143225,

czyli niewiele ponad 300 miliardów, co dla dzisiejszych superkomputerów nie wydaje się oszałamiająco dużą liczbą. Jednakże, jeżeli uwzględnimy losową kolejność samych permutacji, liczba ta ulegnie bardzo istotnemu zwiększeniu. Możemy także pomyśleć o innych rodzajach permutacji.

Michał Szurek

Zobacz także:

Równania, kody, szyfry, matematyka i poezja
Łamigłówki i poważne zadania