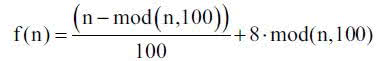Równania, kody, szyfry, matematyka i poezja

Równanie to dla matematyka coś jak szyfr. Rozwiązywanie równań, ta kwintesencja matematyki - to odczytywanie zaszyfrowanego tekstu. Zwracali na to uwagę teologowie od XVI wieku. Jan Paweł II, który znał się na matematyce, pisał kilkakrotnie i o tym, wspominał w swoich homiliach - niestety, konkrety uleciały mi z pamięci.

W nauce szkolnej przedstawia się Pitagorasa jako autora twierdzenia o pewnej zależności w trójkącie prostokątnym. Tak to weszło do naszej, europocentrycznej, filozofii. A przecież Pitagoras ma o wiele większą zasługę. To on narzucił swoim uczniom powinność "poznawania świata", poczynając od tego "co jest za tą górką?", do badania gwiazd. Dlatego to Europejczycy "odkryli" starsze cywilizacje, a nie na odwrót.

Niektórzy Czytelnicy pamiętają "wzory Viète’a"; sporo starszych Czytelników pamięta ze szkoły sam termin i z grubsza to, że kwestia pojawiała się przy równaniach kwadratowych. Te wzory to "ideologicznie" jakby szyfrowanie informacji.

Nic dziwnego: sam François Viète (1540-1603) zajmował się na dworze Henryka IV (pierwszy król francuski z dynastii Bourbonów, 1553-1610) właśnie kryptografią i zdołał złamać szyfr, jakim posługiwali się Anglicy w wojnie z Francją. Odegrał więc podobną rolę, jak polscy matematycy (z Marianem Rejewskim na czele), którzy jeszcze przed drugą wojną światową odkryli tajemnice niemieckiej maszyny szyfrującej Enigma.

Modny temat

No właśnie. Od pewnego czasu w nauczaniu modny jest temat "kody i szyfry". Kilka razy już o tym pisałem, a za dwa miesiące pewnie będzie kolejny odcinek. Tym razem piszę pod wpływem filmu o wojnie 1920 r., gdzie zwycięstwo w dużej mierze zawdzięczamy złamaniu szyfru wojsk bolszewickich przez zespół pod kierunkiem młodego wówczas Wacława Sierpińskiego (1882-1969). Nie, to jeszcze nie Enigma, to tylko wstęp. Pamiętam scenę z filmu, gdzie Józef Piłsudski (grany przez Daniela Olbrychskiego) mówi do dowódcy działu szyfrów:

- Jeżeli to prawda, ma Pan Virtuti Militari. Ale jeżeli nieprawda - będę musiał Pana rozstrzelać.

Rozszyfrowane depesze przynosiły bowiem ważną wiadomość: wojska Tuchaczewskiego nie dostaną wsparcia. Można atakować!

Znałem Wacława Sierpińskiego (o ile tak można powiedzieć: ja byłem młodym studentem, on sławnym profesorem), chodziłem na jego wykłady i seminaria. Robił wrażenie zasuszonego naukowca, roztargnionego, zasiedziałego w swojej dyscyplinie i niewidzącego świata poza nią. Wykładał specyficznie, twarzą do tablicy, nie patrząc na audytorium… ale czuło się, że jest to wybitny specjalista. Miał zresztą specyficzne zdolności matematyczne - takie do rozwiązywania zadań. Są bowiem i inne umysły - uczeni stosunkowo kiepscy w łamigłówkach, za to głęboko rozumiejący całą teorię i potrafiący zapoczątkować całe dziedziny twórczości. Potrzebujemy jednych i drugich - choć szybciej awansują ci pierwsi.

Wacław Sierpiński nigdy nie mówił o swoich dokonaniach w 1920 r. Do 1939 r. na pewno należało jeszcze zachować tajność, a z kolei po 1945 r. nie cieszyli się sympatią ówczesnych władz ci, którzy wojowali z Rosją Radziecką. Sprawdza się moje przekonanie, że uczeni są potrzebni jak wojsko: "w razie czego". Oto prezydent Roosevelt dzwoni do Einsteina:

- Słuchaj, Albert, wygramy z Japonią, ale zginie jeszcze kilka milionów naszych żołnierzy. Zrób bombę!

- Na kiedy, panie prezydencie?

- Jak to na kiedy? Na przedwczoraj!!!

Wybitny rosyjski matematyki Igor Arnold otwarcie i ze smutkiem mówił, że wojna ma duży wpływ na rozwój matematyki i fizyki (rakiety, komputery, radar, a i GPS ma proweniencję militarną). Nie wchodzę w moralny aspekt użycia bomby atomowej: tu przedłużenie wojny o rok i śmierć kilku milionów własnych żołnierzy - tam cierpienia niewinnej ludności cywilnej.

***

Uciekam na swojskie obszary - do matematyki. Wielu z nas bawiło się szyframi, może w harcerstwie, może tak po prostu. Proste szyfry, oparte na zasadzie zamiany liter na inne litery albo inne cyfry, łamiemy standardowo - jeżeli tylko uchwycimy kilka wskazówek (np. zgadniemy imię króla). Dziś pomaga w tym jeszcze analiza statystyczna. Gorzej, gdy wszystko jest zmienne. Ale najgorzej, gdy nie ma żadnej regularności. Weźmy pod uwagę szyfr opisany w "Przygodach dzielnego wojaka Szwejka". Bierzemy książkę, np. "Potop". Oto początkowe zdania z pierwszej i drugiej strony.

Chcemy zaszyfrować słowo "KOT". Otwieramy na stronie 1 i sąsiadującej drugiej. Odnajdujemy, że na stronie 1 litera K pojawia się po raz pierwszy na 59 miejscu. Znajdujemy pięćdziesiąte dziewiąte słowo na przeciwległej, drugiej stronie. Jest nim wyraz "a". Teraz litera O. Na lewej stronie jest n a 16 miejscu, a szesnastym słowem po prawej jest "pana". Litera T jest na 95 miejscu, o ile dobrze policzyłem, a dziewięćdziesiątym piątym słowem po prawej jest wyraz "o". Zatem KOT = 1 A PANA O.

Szyfr "nie do odgadnięcia", chociaż straszliwie powolny i do szyfrowania, i… odgadywania. Załóżmy, że chcemy przekazać literę M. Możemy sprawdzić, że szyfrujemy ją za pomocą słowa "Wołodyjowski". I już po nas, już nam szykują celę więzienną. Możemy tylko liczyć na wymianę szpiegów! Oprócz tego kontrwywiad odnotowuje meldunki tajnych współpracowników, że od pewnego czasu klienci kupują chętnie pierwszy tom "Potopu".

Artykuł mój jest przyczynkiem do takiej tezy: nawet najbardziej dziwaczne pomysły matematyków mogą znaleźć zastosowanie w szeroko pojmowanej praktyce. Czy np. można sobie wyobrazić mniej przydatne odkrycie matematyczne niż cecha podzielności… przez 47?

Kiedy nam w życiu będzie potrzebna? A jeśli nawet, to prościej będzie spróbować podzielić. Jeżeli się podzieli, to dobrze, jeżeli nie, to… drugie dobrze (wiemy, że się nie dzieli).

Jak dzielić i po co

Po tym wstępie przejdźmy już do matematyki. Czy znacie, Czytelnicy, jakieś cechy podzielności? Na pewno. Liczby parzyste mają na końcu 2, 4, 6, 8 albo zero. Liczba jest podzielna przez trzy, kiedy suma jej cyfr jest podzielna przez trzy. Podobnie z cechą podzielności przez dziewięć - suma cyfr ma być podzielna przez dziewięć.

Po co to komu? Skłamałbym, gdybym przekonywał Czytelnika, że się to do czegoś nadaje poza… zadaniami szkolnymi. No, jeszcze cecha podzielności przez 4 (a jaka ona jest, Czytelniku? Może zastosujesz, gdy będziesz się chciał dowiedzieć, w którym roku wypadają Igrzyska kolejnej Olimpiady…). Ale cecha podzielności przez 47? To już jakieś zawracanie głowy. Czy kiedykolwiek będziemy sprawdzać, że coś dzieli się przez 47? A jeśli nawet, to weźmiemy wówczas kalkulator i zobaczymy.

Tak jest. Masz rację, Czytelniku. A jednak czytaj dalej. Bardzo proszę.

Cecha podzielności przez 47: Liczba 100a + b dzieli się przez 47 wtedy i tylko wtedy, gdy przez 47 podzielna jest liczba a + 8b.

Matematyk się uśmiechnie z zadowoleniem: "ojej, ładne". Ale matematyka to matematyka. Liczą się dowody i zwracamy uwagę na ich piękno. Jak udowodnić naszą cechę? Bardzo prosto. Odejmijmy od 100a + b liczbę 94a - 47b = 47(2a – b). Otrzymamy 100a + b – 94a + 47b = 6a + 48b = 6(a + 8b).

Odjęliśmy liczbę podzielną przez 47, a więc jeśli 6(a + 8b) jest podzielna przez 47, to i 100a + b też. Ale liczba 6 jest względnie pierwsza z 47, a z tego wynika, że 6(a + 8b) jest podzielna przez 47 wtedy i tylko wtedy, gdy podzielna jest a + 8b. Koniec dowodu.

Zobaczmy kilka przykładów.

Czy 8805685 jest podzielna przez 47? Jeśli to nas naprawdę interesuje, to szybciej dowiemy się, po prostu dzieląc, choćby tak, jak nas nauczono w szkole podstawowej. Zresztą w każdym telefonie komórkowym jest teraz kalkulator. Dzieli się? Tak, ilorazem jest 187355.

No, to zobaczmy, co nam powie cecha podzielności. Odczepiamy dwie ostatnie cyfry, mnożymy je przez 8, wynik dodajemy do "uciętej liczby" i z otrzymaną liczbą robimy to samo.

8805685 → 88056 + 8·85 = 88736 → 887 + 8·36 = 1175 → 11 + 8·75 = 611 →6 + 8·11 = 94.

Możemy zauważyć, że 94 jest podzielne przez 47 (ilorazem jest 2), zatem nasza wyjściowa liczba też. No, dobrze. Ale co by było, gdybyśmy bawili się dalej?

94 → 0 + 8·94 = 752 → 7 + 8·52 = 423 → 4 + 8·23 = 188 → 1 + 8·88 = 705 → 7 + 8·5 = 47.

Teraz musimy przestać. Czterdzieści siedem dzieli się przez 47, prawda?

Czy naprawdę musimy przestać? A co by było, gdybyśmy pociągnęli procedurę dalej? Ojej, będzie się działo… Oszczędzę szczegółów. Może tylko początek:

47 → 0 + 8·47 = 376 → 3 + 8·76 = 611 → 6 + 8·11 = 94 → 0 + 8·94 = 752.

Ale, niestety, to wciąga jak gryzienie pestek słonecznika…

752 → 7 + 8·52 = 423 → 4 + 8·23 = 188 → 1 + 8·88 = 705 →7 + 8·5 = 47.

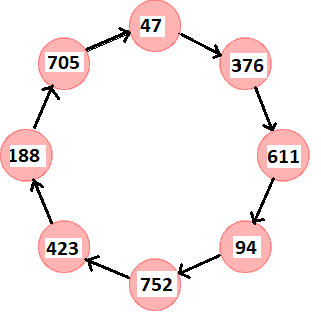
Ach, czterdzieści siedem. To już było. Co będzie dalej? Da capo. To samo. Liczby chodzą w takiej pętli:

To w gruncie rzeczy ciekawe. Takie pętelki liczbowe.

Dwa następne przykłady.

Chcemy dowiedzieć się, czy 10017627 dzieli się przez 47. Po co nam ta wiedza? Pamiętamy o zasadzie: biada wiedzy, która nie pomaga wiedzącemu. Wiedza zawsze ma być po coś. Będzie po coś, ale teraz nie będę się tłumaczył. Jeszcze trochę rachunków:

10017627 → 100176 + 8·27 = 100392.

"Zamienił stryjek siekierkę na kijek". Co z tego wszystkiego mamy?

No cóż, iterujmy postępowanie. To znaczy: róbmy tak dalej (to znaczy słowo "iterować").

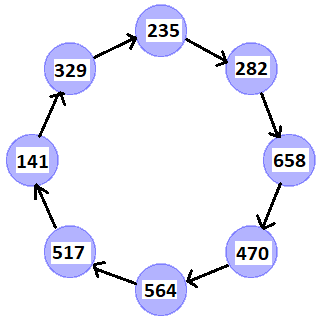
100392 → 1003 + 8·92 = 1739 → 17 + 8·39 = 329 → 3 + 8·29 = 235.

Przerwijmy zabawę, podzielmy, jak w szkole (albo kalkulatorem): 235 = 5·47. Bingo. Wyjściowa liczba 10017627 dzieli się przez 47.

Brawo my!

A co by było, gdyby pójść dalej? Możecie wierzyć, możecie sprawdzić.

I jeszcze jedna ciekawostka. Chcemy sprawdzić, czy 799 dzieli się przez 47. Stosujemy cechę podzielności. Odczepiamy dwie ostatnie cyfry, tak otrzymaną liczbę mnożymy przez 8 i dodajemy do tego, co zostało:

799 → 7 + 8·99 = 7 + 792 = 799.

Co mamy? Liczba 799 dzieli się przez 47 wtedy i tylko wtedy, gdy 799 dzieli się przez 47? No tak, to racja, ale żadnej matematyki do tego nie potrzeba!!! Masło jest maślane (w każdym razie to masło, które jest maślane).

O liściu, piratach i końcu żartów!

Jeszcze dwie przypowieści. Gdzie najlepiej schować liść? Odpowiedź jest oczywista: w lesie! Ba, tylko jak go potem znaleźć?

A drugą znamy z czytywanych dawno temu książek pirackich. Piraci sporządzali mapę, gdzie zakopali skarb. Inni ją kradli, albo zdobywali w walce. Ale na mapie nie było napisane, jakiej wyspy dotyczy. I szukaj sobie! Oczywiście piraci sobie radzili (tortury) - szyfry o których mówię, też można wydobyć takimi metodami.

Koniec żartów. Czytelniku! Tworzymy szyfr. Jestem tajnym szpiegiem i używam "Młodego Technika" jako skrzynki kontaktowej. Przekazuj szyfrowane wiadomości do mnie w następujący sposób.

Najpierw zamień tekst na ciąg liczb, za pomocą kodu: AB C D E F G H IJ K L M N OP R S T UWX Y Z1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Jak widzisz, nie używamy polskich znaków diakrytycznych (czyli bez ą, ę, ć, ń, ó, ś) oraz niepolskich q, v – ale niepolski x na wszelki wypadek został. Dołączmy jeszcze 25 jako spację (przerwę między wyrazami). Aha, najważniejsze. Zastosuj, proszę, kod nr 47.

Wiesz, co to znaczy. Idziesz do znajomego matematyka.

- Podaj mi cechę podzielności przez 47.

Znajomy wytrzeszcza oczy ze zdumienia.

- Po co ci to?

Odpowiadasz dumnie:

- Nie mogę ci powiedzieć, to tajemnica!!!

Matematyk podaje Ci tę cechę… i już wiesz, że do szyfrowania służy niepozornie wyglądająca funkcja

bo takim wzorem jest opisane działanie

100a + b → a + 8b.

A zatem, gdy chcesz dowiedzieć się, co znaczy w zaszyfrowanym komunikacie liczba np. 77777777, stosujesz funkcję

100a + b → a + 8b

tak długo, aż otrzymasz liczbę od 1 do 25. Teraz spójrz na jawny kod litera-liczba. Zobaczmy: 77777777 →… zostawiam to Tobie, jako zadanie. Zobaczmy jednak, jaką literę kryje 48? Czytajmy:

48 → 0 + 8·48 = 384.

Potem dostaniemy kolejno:

384 → 3 + 8·84 = 675 → 6 + 8·75 = 606 → 6 + 8·6 = 54 → 0 + 8·54 = 432…

Końca nie widać. Dopiero za sześćdziesiątym (!) razem pojawi się liczba mniejsza od 25. Jest to liczba 3, a zatem 48 to litera C.

A co daje nam ten komunikat? (przypominam, że posługujemy się szyfrem nr 47):

80 – 152 – 136 – 546 – 695719 – 100 – 224 – 555 – 412 – 111 – 640 – 102 – 152 – 12881 – 444 – 77777777 – 59 – 408 – 373 – 1234567 – 341.

No, myślisz sobie, co w tym trudnego, trochę rachunków. Zaczynamy. Na początku jest 80. Reguła znana:

80 → 0 + 8·80 = 640 → 6 + 8·40 = 326.

Dalej jest tak:

326 → 211 → 90 → 720 → 167 → 537 → 301 → 11.

Jest! Pierwszą literą depeszy jest K. Uff , łatwe, ale ile czasu to trwa?

Zobaczmy jeszcze, ile będziemy się trudzić z liczbą 1234567. Dopiero za szesnastym razem dostaniemy liczbę mniejszą od 25, a mianowicie 12. Czyli 1234567 to L.

No dobrze, mówi ktoś, ale ta operacja arytmetyczna jest tak prosta, że zaprogramowanie jej na komputer pozwoli złamać szyfr natychmiast. Tak, to prawda. To są łatwe obliczenia dla komputera. Pomysł z szyfrem publicznym polega zaś na tym, żeby obliczenia były trudne i dla komputera. Niech sobie pracuje nawet sto lat. Odszyfruje wiadomość? Nie szkodzi. Dawno już nie będzie to mieć znaczenia. Na tym (bardzo mniej więcej) polegają szyfry publiczne. Można je złamać, jeżeli będziemy pracować bardzo długo… aż wiadomości przestaną być aktualne.

Broń zawsze rodziła "antybroń". Zaczęło się od miecza i tarczy. Tajne służby płacą uzdolnionym matematykom wielkie sumy, żeby wymyślali takie metody szyfrowania, których komputery (wraz z tymi, które zbudujemy) nie złamią i w XXII wieku.

Dwudziesty drugi wiek? Nie tak trudno przekonać się, że jest już na świecie wiele osób, które będą żyć w tym, oby wspaniałym, wieku!

Aha, aha? A co będzie, gdy poproszę (ja, Tajny Współpracownik, kontakt przez "Młodego Technika") o szyfrowanie kodem nr 23? Albo 17? Proste:

- Cześć, Rysiek, przepraszam, że dzwonię tak późno. Nic nie szkodzi? To dobrze? Słuchaj, jaka jest cecha podzielności przez 23? Nie, nie mogę powiedzieć, po co mi to? Czy zainteresowałem się matematyką? W pewnym sensie tak. Podaj mi na wszelki wypadek cechy podzielności przez inne liczby. Może przez 1543? Musisz popracować, żeby ją znaleźć? To znaczy, że nikt jej przedtem nie wynalazł? Tym lepiej! Słuchaj, może ocaliłeś nasz kraj!

Obyśmy nigdy nie musieli stosować matematyki w takich celach.

***

W tytule artykułu jest i o poezji. Co ona ma z tym wspólnego?

Jak to co? Poezja też szyfruje świat.

Jak?

Swoimi własnymi metodami - podobnymi do algebraicznych.