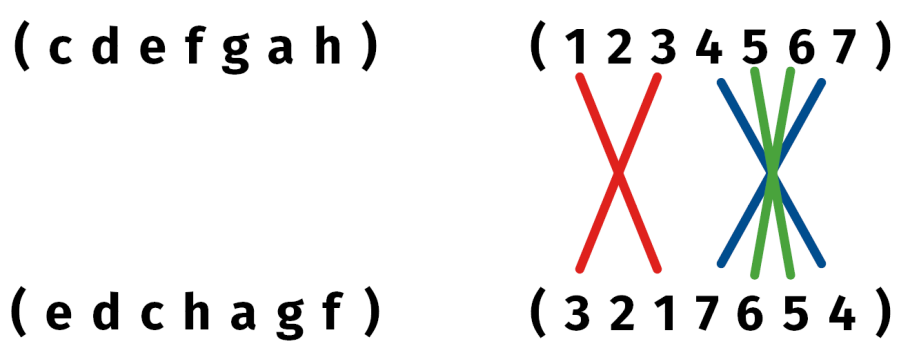Cechy wspólne matematyki i muzyki

Obiecałem mojemu przyjacielowi, Kazimierzowi Skurzyńskiemu, esej na temat "Dyskretny urok liczb pierwszych", podobny do artykułu o liczbach nieparzystych i ich "dyskretnym" wdzięku. Poczekasz, Kaziu, jeszcze miesiąc? Zdarzyło się bowiem, że zachwyciłem się krótkim, prostym, ale matematycznie finezyjnym walcem w tonacji a-moll, napisanym przez znajomą, panią Jolę. Na początek wstęp (chociaż nie wiem, czy pogłębiona analiza matematyki tej kompozycji będzie dla Czytelników dostatecznie interesująca). Ciekawi mnie zresztą, na ile Autorka zdaje sobie sprawę, że weszła w algebrę, matematykę dyskretną, teorię grup i kryptografię!
Obrazki z muzycznej wystawy
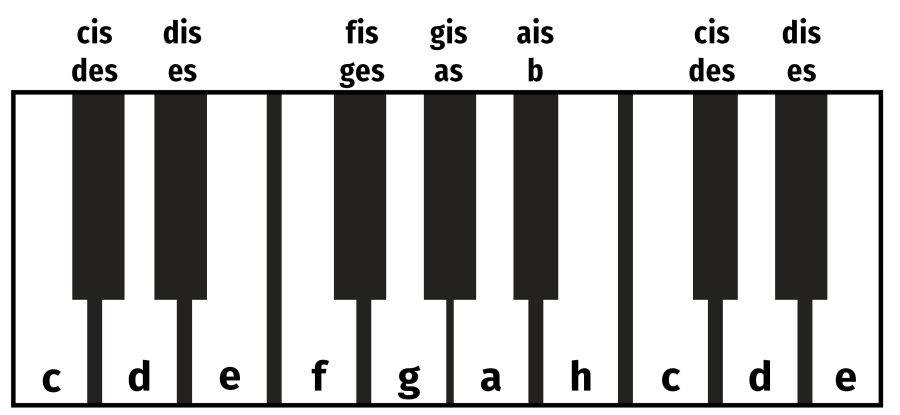
Najpierw proponuję obrazki matematyczno-muzyczne, a dla niewykształconych muzycznie Czytelników przypomnienie nazw nut (1).
Jest jeszcze tyle pięknej muzyki
do napisania w C-dur.
(Wojciech Młynarski, w piosence dedykowanej Jerzemu Wasowskiemu)
Zacznę "od pieca", czyli kilku przykładów z pogranicza matematyki i muzyki.
Przypomnę, że oktawa to odstęp między wysokościami dźwięków odpowiadającymi skróceniu drgającej struny o połowę. "Jakoś tak jest", że dla ucha ludzkiego dźwięk w oktawie to "ten sam, tylko wyższy", podczas gdy po skróceniu struny, np. o jedną trzecią, słyszymy wyraźnie "co innego". Na fortepianie oktawa to odstęp między dwoma klawiszami c.
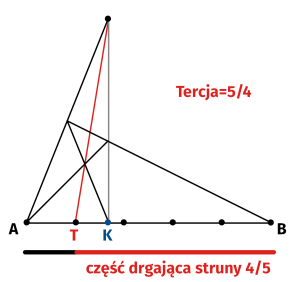
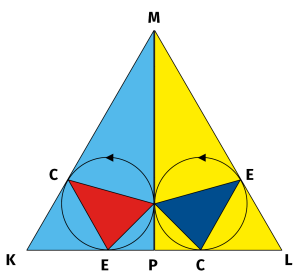
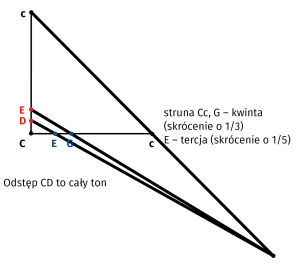
Pierwszy rysunkowy przykład (2) to "harmoniczny podział oktawy (a więc kwinta)" i "harmoniczny podział kwinty (= tercja)". Każdy muzyk wie, że tak jest i się z tym zgodzi, a każdy matematyk zna podział odcinka w stosunku skrajnym i średnim oraz bardzo elegancką konstrukcję Desarguesa czwartego harmonicznego (i to konstrukcję typu Mascheroniego - samą linijką). Mało kto jednak widzi, że to to samo.
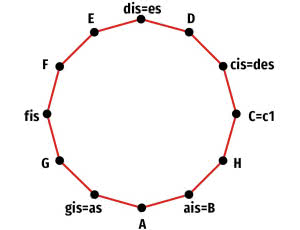
Jeżeli nie wychodzimy poza oktawę, to klawiaturę fortepianu można traktować jako linię prostą, nawiniętą na okrąg (3). W terminologii matematycznej takie nawijanie nazywa się odwzorowaniem Hopfa - ale nie jest to nic innego, niż to, co robimy na co dzień, odmierzając godziny od zerowej do dwunastej. Jeżeli od ósmej upłynie sześć godzin, to jest druga. Czyżby 8+6=2? Tak, w tej arytmetyce tak!
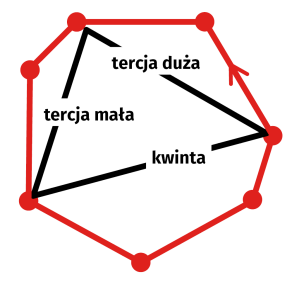
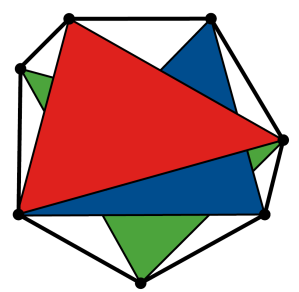
No dobrze. Gama durowa to ciąg ośmiu dźwięków o odległościach kolejno: 1, 1, ½, 1, 1, 1, ½. Odpowiada to siedmiokątowi o interesującym kształcie (4).
Na zakończenie "obrazków z wystawy" zdumiewająca ilustracja muzyczna najważniejszego twierdzenia geometrii rzutowej (czyli geometrii perspektywy zbieżnej) - widoczna na rys. 7.
Twierdzenie (Desargues, ok. 1660). Jeżeli dwie czwórki punktów są harmonicznie sprzężone, to jeden z nich powstaje z drugiego przez rzutowanie środkowe!
Taniec wirowy z metrum ¾ - Walc pani Joli
Przechodzimy do walca. Jako matematyk, zacznę od definicji. Jest to taniec wirowy, z metrum ¾ (trzy ćwierćnuty na takt), wywodzący się z niemieckich tańców ludowych. Dopiero w 1786 r. zagrano po raz pierwszy walca na wielkiej scenie operowej w Wiedniu i od tej pory szybko zdobył on pozycję tańca bardzo uroczystego, nie tracąc swej ludyczności.
Czy ktoś zna Jacquesa Brela "Walc na tysiąc pas"? Polecam znaleźć na YouTubie.
A przepiękny walc Zygmunta Koniecznego do słów Juliana Tuwima ("Kwiaty polskie") w przejmującym wykonaniu Ewy Demarczyk?
Spójrzmy teraz na sam początek walca, o którym tu mowa (8). Podłożone słowa są moim wymysłem na potrzeby tego artykułu.
Najpierw sprawdźmy, czy zgadzają się ułamki. Melodia jest na trzy czwarte, czyli w takcie mamy trzy ćwierćnuty. Liczymy: nie zgadza się. Już w pierwszym mamy
Jak pamiętamy ze szkoły podstawowej
Sytuację ratuje jednak niepozorny znak na początku: pauza ósemkowa. Pauzy liczą się do biegu melodii, to dość oczywiste.
W dziale matematyki zwanej matematyką dyskretną ważne są permutacje. To po prostu przestawianki: brak - bark, rolka - karol - koral - lokra - kralo - oakrl. Ostatnie trzy słowa nic nie znaczą, ale nie o to chodzi w permutacjach. Matematyk woli przestawiać liczby. Może ktoś pamięta ze szkoły, że permutacji siedmiu liczb 1, 2, 3, 4, 5, 6, 7 jest aż 5040 (tzw. liczba platońska)?
No właśnie. Już w pierwszych dwóch taktach mamy permutację nut oktawy. Kompozytorka zmieniła kolejność, ale nic nie dodała, nic nie ujęła. Przełóżmy to na liczby, żeby było prościej (co matematyka, to matematyka) - rys. 10.
Można powiedzieć, że kompozytorka złamała tu naturalną opadającą kolejność dźwięków, przenosząc je od czwartego o oktawę wyżej. Dla muzyka to fraszka, ale matematycznie rzecz jest całkiem skomplikowana. W skali temperowanej (dla matematyka: dyskretnej, w przeciwieństwie do nietemperowanej, czyli ciągłej) sekwencja opadająca to ciąg geometryczny o ilorazie
(odwrotność dwunastego pierwiastka z dwóch), a przejście o oktawę wyżej to mnożenie przez 2. Mam tu na myśli częstość, czyli liczbę drgań na sekundę (a więc herców).
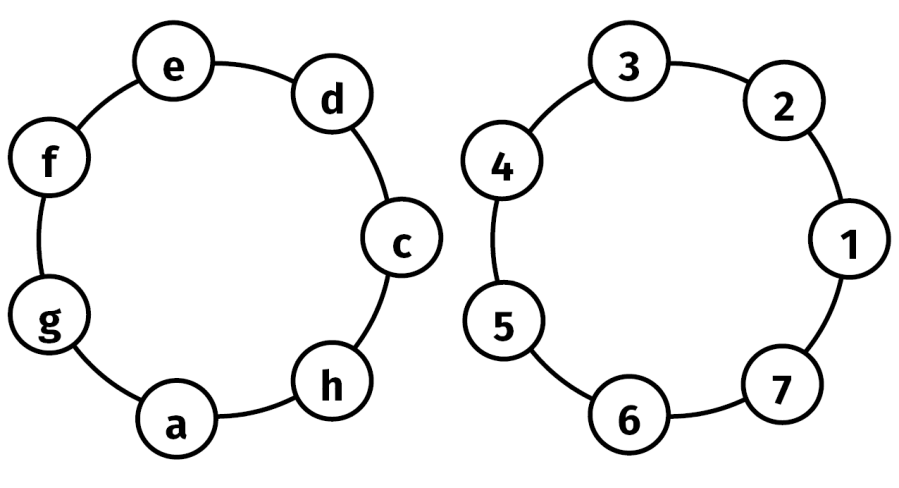
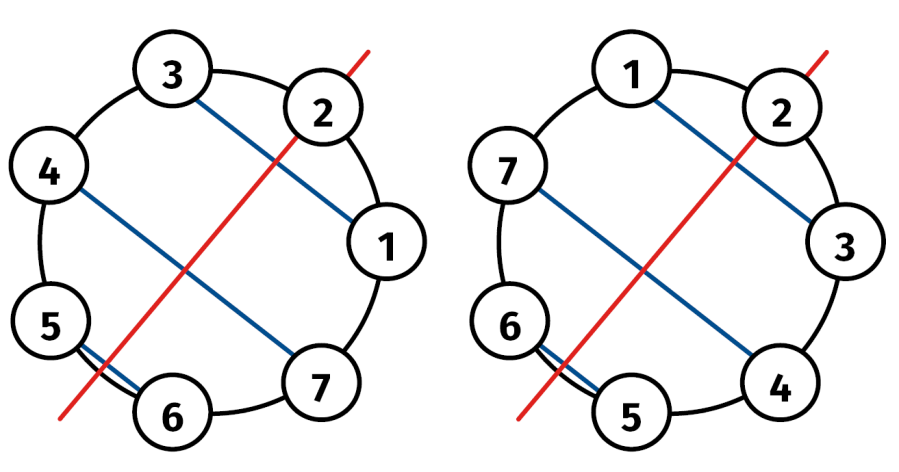
Przedstawmy jeszcze inaczej tę permutację. Zamieniamy 1 z 3, 4 z 7 oraz 5 i 6 (11). Jest to kolejność dźwięków początkowej frazy naszego walca. Oczywiście ważne są też długości dźwięków, ale tym zajmiemy się w dalszej części.
Co to za przekształcenie geometryczne (11)? Oczywiście: symetria względem zaznaczonej ukośnej prostej czerwonej! Wierzę w Pitagorasa: fraza jest muzycznie tak ładna dlatego, że pochodzi od jednego z najprostszych i najważniejszych przekształceń matematycznych: symetrii osiowej. Proste jest piękne. Piękno jest proste.
Sprawa nadaje się na egzamin z matematyki na studiach. Jakie własności ma permutacja s=(3217654)? Mógłbym dać takie zadanie:
- Rozłóż s na cykle. Odpowiedź: są cztery
- Oblicz 2019 potęgę permutacji s.
- Wyznacz, na którym miejscu wśród wszystkich permutacji znajduje się s. Zrób to dla porządku leksykograficznego (odpowiedź: 1584) i indukcyjnego (odpowiedź: 144)
O, proszę. Mam zadania dla studentów (ale dopiero na wiosenny semestr). Ze względu jednak na to, że "Młody Technik" nie jest wyłącznie do mojej dyspozycji, nie wejdę w szczegóły. Studenci: czy zdarza się, żeby wykładowca podawał zadania przed kolokwium?
W następnych dwóch taktach widzimy następstwo nut przesunięte o 1 w prawo. Przypomina to znany w teorii kodowania "szyfr Cezara". Dla utajnienia informacji przesuwamy wszystkie litery o jedną lub kilka w prawo (zamiast a bierzemy b, zamiast b piszemy c itd). Fraza BACA PASIE OWCE stanie się wtedy ciągiem CBDB RBTJF PXDF - jeżeli nie będziemy uzwględniać polskich znaków diakrytycznych, czyli naszych ą, ć, ę, ł, ń, ó, ś, ż, ź. To bardzo prosty szyfr, choć można go tak skomplikować, że nawet dzisiaj nadawać się będzie do szyfrowania depesz dyplomatycznych.
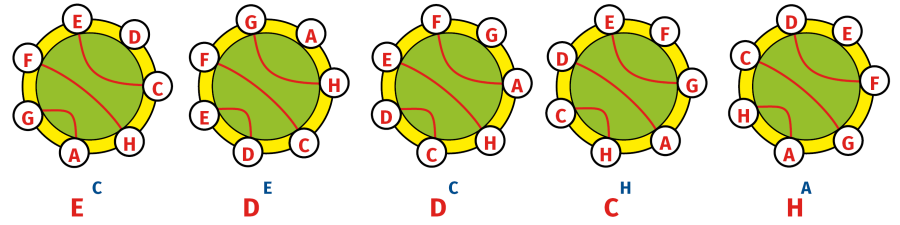
Oto przykład. Chcemy za pomocą naszego "Walca o burym kotku" zaszyfrować słowo "cecha". Tworzymy, np. z tektury, przyrząd złożony z wewnętrznego zielonego kółka i żółtego pierścienia z zaznaczonymi literami.
Całość jest rozcięta po obwodzie wewnętrznego kółka. Zewnętrzny pierścień może się wobec tego obracać po zielonym. Wygodniej jest zresztą zrobić pełne żółte kółko i usadzić je na wspólnej osi z zielonym. Ustawiamy przyrząd w położeniu wyjściowym. Przy pierwszym połączeniu litera C łączy się z E. Obracamy pierścień o jedną siódmą pełnego obrotu. Druga litera słowa "cecha", czyli E, łączy się teraz z D. Po następnym obrocie mamy połączenie C-D. I na tym zasadza się zmyślność metody. Nie ma sztywnego przyporządkowania liter, jak w dziecięcych szyfrach harcerskich. Zmienność może być opisana… właśnie pierwszymi taktami piosenki.
Wydaje się to też dość proste. I jest proste. Ale tak właśnie działała słynna niemiecka maszyna szyfrująca Enigma. Liter było w niej oczywiście nie 7, a tyle, ile w alfabecie, i połączenia nie okazywały się tak proste. Zasada była jednak taka sama. Trzeba było tylko wybrać permutację.
Lżej kończ waść fugę i spłódź hymn trąb!
Co to znaczy? No, jak to? Jakiś kompozytor zabrnął niepotrzebnie w didaskalia przy fudze, a jeszcze trzeba napisać uroczyste zakończenie. Tak, tak, ale czy ma to jakikolwiek związek z artykułem? Nie widać? W tym zdaniu (autorstwa Juliana Tuwima) są wszystkie litery języka polskiego, każda po razie. Permutacja! Kolejny przykład na związki matematyki i muzyki. Matematyka jest wszędzie, a muzyka łagodzi obyczaje.
Jak może Czytelnicy się zorientowali, nie wyszedłem poza analizę czterech pierwszych taktów walca. O pozostałych - może innym razem.
Przyda się i w lidze
Miałem już kończyć pisanie, ale coś mi wciąż chodziło po głowie. Pamiętałem, że gdzieś już widziałem rysunek przypominający te, oznaczone jako 11 i 12. Ależ tak! Przypomniałem sobie: sam o tym pisałem w książce sprzed dziesięciu lat. Chodzi o… rozstawienie drużyn piłkarskich w rozgrywkach ligowych. Ten sam schemat.
Wyobraźmy sobie, że w lidze występuje tylko siedem zespołów z następujących miejscowości: Chrzanów, Drawsko, Ełk, Frombork, Gliwice, Aleksandrów i Hajnówka. Patrzymy na pierwszy element z rys. 12. Drawsko ma wolny termin, Ełk gra z Chrzanowem, Frombork z Hajnówką, a Aleksandrów z Gliwicami. Obracamy pierścień zewnętrzny, jak przy szyfrowaniu. Odpoczywa Aleksandrów, Gliwice jadą do Hajnówki, Frombork potyka się z Chrzanowem, Ełk z Drawskiem itd. Teoria permutacji gwarantuje, że system działa.
Jak każdy chłopiec, grywałem w piłkę nożną. W drużynie podwórkowej byłem bramkarzem. Obecnie gra ta polega jednak chyba na czym innym niż kiedyś. Do końca nie wiem, ale reklamy telewizyjne przedstawiają ją jednoznacznie. Chodzi o to, żeby… trafić w słupek, bo wtedy jest okazja do… napicia się piwa.
Kompozytorce, której walc posłużył mi jako temat artykułu, może być jednak przykro, że jej utwór może być wykorzystywany i przez Zbigniewa Bońka, i jego sztab. A może wprost przeciwnie: przyjemnie?
Muzyka towarzyszy nam od początku do końca życia.
Zobacz także:
Wycieczka w nierzeczywisty świat matematyki
Myślenie ma kolosalną przyszłość