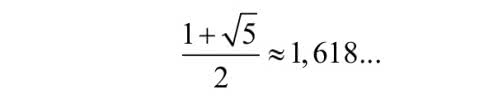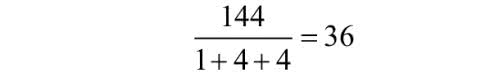SU DO KU, czyli: SpróbUj, DOKąd Umiesz - część 2
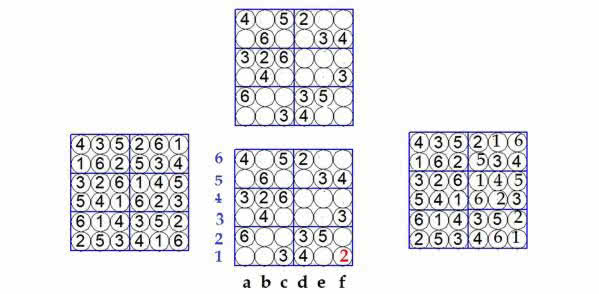
Na rys. 1 widzimy tę łamigłówkę w łatwiejszej wersji, czyli kwadrat 6×6, podzielony na prostokąty 2×3. Wstawiamy weń liczby 1, 2, 3, 4, 5, 6 - tak, by nie powtarzały się ani w pionie, ani w poziomie, ani w każdym z wyróżnionych sześciokątów.
Spróbujmy rozwiązać sudoku widoczne w górnym kwadracie. Czy można uzupełnić go liczbami od 1 do 6, zgodnie z ustalonymi dla tej gry regułami? Można - ale niejednoznacznie. Zobaczmy - dopełniamy do kwadratu po lewej, albo do kwadratu po prawej.
Można powiedzieć, że to nie jest baza do łamigłówki. Na ogół zakładamy, że łamigłówka ma jedno rozwiązanie. Zadanie znalezienia różnych baz dla "dużego" sudoku, czyli 9×9, jest trudnym zadaniem i nie ma szans na jego pełne rozwiązanie.
Jeszcze jedna ważna zależność - układ sprzeczny. Środkowego dolnego kwadratu (tego z liczbą 2 w prawym dolnym narożniku) nie da się uzupełnić do całości. Dlaczego?
Zabawy i dygresje
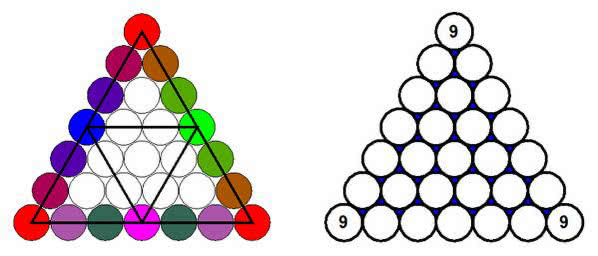
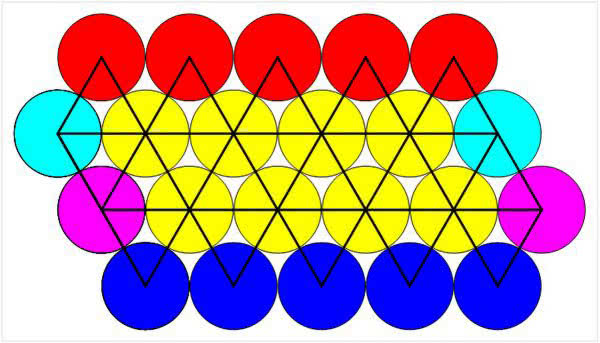
Pobawmy się dalej. Skorzystajmy z intuicji dzieci. One czują, że zabawa to wstęp do nauki. Wyjdźmy w przestrzeń. Czy na rys. 2 każdy widzi siatkę czworościanu, zbudowanego z kuleczek, np. piłeczek pingpongowych? Przypomnijmy sobie szkolne lekcje geometrii. Kolory po lewej stronie rysunku wyjaśniają, co się do czego dokleja przy składaniu bryły. W szczególności trzy narożne (czerwone) kulki zostaną sklejone w jedną. Dlatego ma w nich stać ta sama liczba. Może nią być 9. Dlaczego? A dlaczego nie?
Aha, nie sformułowałem przecież zadania. Brzmi ono tak: czy można w widoczną siatkę wpisać liczby od 0 do 9 tak, by każda ściana zawierała wszystkie liczby? Zadanie nietrudne, ale ile trzeba sobie wyobrazić! Nie będę psuł przyjemności Czytelnikom i rozwiązania nie podam.
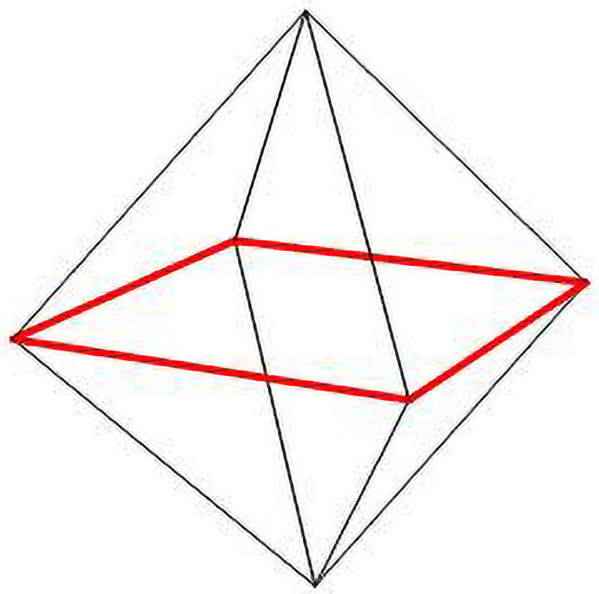
Bardzo ładną i niedocenianą bryłą foremną jest ośmiościan foremny, zbudowany z dwóch piramidek (= ostrosłupów) o podstawie kwadratowej. Jak sama nazwa wskazuje, ośmiościan ma osiem ścian.
Wierzchołków w ośmiościanie jest sześć. To przeciwnie niż w sześcianie, który ma sześć ścian i osiem wierzchołków. Krawędzi obie bryły mają tyle samo - po dwanaście. Są to bryły dualne - co znaczy, że łącząc środki ścian sześcianu, dostaniemy ośmiościan, a środki ścian ośmiościanu dadzą sześcian. Obydwie te bryły spełniają ("bo muszą") wzór Eulera: suma liczby wierzchołków i liczby ścian przewyższa o 2 liczbę krawędzi.
Zadanie 1. Najpierw zapisz ostatnie zdanie poprzedniego akapitu wzorem matematycznym. Na rys. 3 widzisz siatkę ośmiościanu, również takiego zbudowanego z kuleczek. Każda krawędź ma cztery kulki. Każda ściana jest trójkątem o dziesięciu kulkach. Zadanie narzuca się samo: czy da się wpisać w kółka siatki liczby od 0 do 9 tak, by po sklejeniu bryły każda ściana zawierała wszystkie liczby (z tego już wynika, że bez powtórzeń). Tak jak poprzednio, największą trudnością w tym zadaniu jest wyobrażenie sobie, jak z siatki powstaje bryła. Nie umiem tego wytłumaczyć słowami pisanymi, więc i tu rozwiązania nie podam.
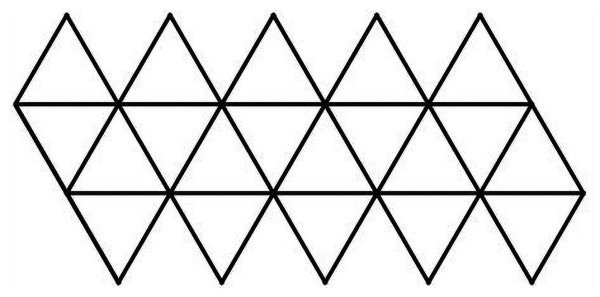
Już Platon (a żył w V-IV wieku p.n.e.) znał wszystkie wielościany foremne: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan. Zastanawiające, jak do tego doszedł - bez ołówka i papieru, długopisu, książek, smartfonu i Internetu! O dwunastościanie mówić tu nie będę. Za to sudoku na dwudziestościanie jest interesujące. Widzimy tę bryłę na ilustracji 4, a jej siatkę na rys. 5.
Podobnie jak i poprzednio, nie jest to siatka w sensie, jaki pamiętamy (?!) ze szkoły, a sposób sklejenia trójkątów utworzonych z piłeczek (kulek).
Zadanie 2. Ile kulek potrzeba na złożenie takiego dwudziestościanu? Czy następujące rozumowanie pozostaje poprawne: ponieważ każda ściana jest trójkątem, więc skoro ma być 20 ścian, to potrzeba aż 60 kul?
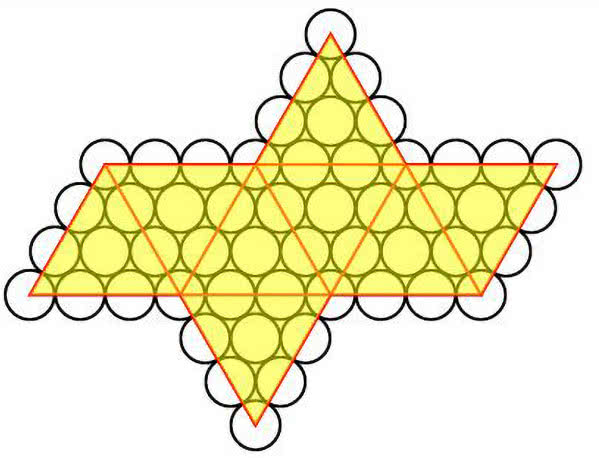
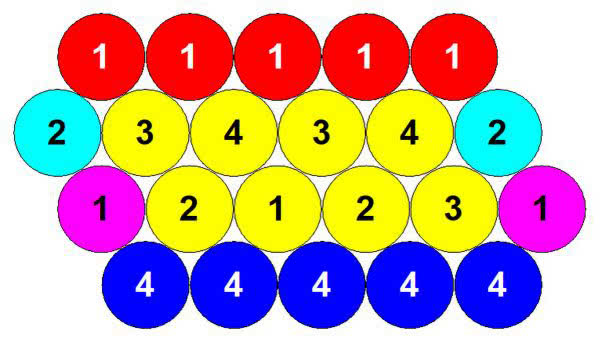
Nietrudno się przekonać, że trzy liczby w dwudziestościanie nie wystarczą. Dokładniej: nie da się ponumerować wierzchołków liczbami 1, 2, 3 tak, by na każdej ścianie (trójkątnej) występowały te trzy liczby, a nie byłoby powtórzeń. A czy da się czterema liczbami? Tak, to jest możliwe! Spójrzmy na rys. 6 i 7.
Zadanie 3. Z czterech liczb można wybrać trzy na cztery sposoby: 123, 124, 134, 234. Znajdź po pięć takich trójkątów w dwudziestościanie z rys. 7 (a także z ilustr. 4).
Zadanie 4 (potrzebna jest bardzo dobra wyobraźnia przestrzenna). Dwudziestościan ma dwanaście wierzchołków, a zatem można go skleić z dwunastu kulek (rys. 7). Przekonaj się, że są trzy wierzchołki (= kulki) oznaczone numerem 1, trzy oznaczone numerem 2 i tak dalej. Kulki jednego koloru tworzą zatem trójkąt. Jaki to trójkąt? Może równoboczny? Spójrz znowu na ilustr. 4.
Następne zadanie jest dla dziadka/babci oraz wnuka/ wnuczki. Rodzice ostatecznie też mogą spróbować swoich sił, ale potrzebują cierpliwości, no i czasu.
Zadanie 5. Kup dwanaście (a lepiej 24) piłeczek pingpongowych, trochę farb w czterech kolorach, pędzelek i odpowiedni klej – nie polecam tych błyskawicznych, typu Superglue czy Kropelka, bo za szybko schną, no i są niebezpieczne dla dzieci. Sklej dwudziestościan. Ubierz wnuczka/wnuczkę w koszulkę, która zaraz potem pójdzie do prania (albo do wyrzucenia). Nakryj stół folią (lepsze niż gazety). Pomalujcie starannie dwudziestościan czterema kolorami 1, 2, 3, 4 - jak na rys. 7. Można zmienić kolejność - najpierw pomalować piłeczki, a potem sklejać. W tym przypadku trzeba zostawić niezamalowane malutkie kółeczka, żeby nie kleić farby do farby.
Teraz najtrudniejsze zadanie (a raczej cały ich ciąg).
Zadanie 6 (a raczej ogólny temat). Zbuduj dwudziestościan taki, jak czworościan i ośmiościan na rys. 2 i 3 - to znaczy, że na każdej krawędzi mają być cztery kulki (piłeczki). W tej wersji zadanie jest i pracochłonne, i nawet kosztowne. Zacznijmy od wyliczenia, ile piłeczek potrzeba. Każda ściana ma dziesięć kulek, zatem do dwudziestościanu potrzeba dwustu? Nie! Musimy pamiętać, że wiele kulek jest wspólnych. Ile krawędzi ma dwudziestościan? Da się to pracowicie policzyć, ale od czego wzór Eulera?
w–k+s=2
gdzie w, k, s są odpowiednio liczbami wierzchołków, krawędzi i ścian. Pamiętamy, że w=12, s=20, a zatem k=30. Mamy 30 krawędzi dwudziestościanu. Można do tego dojść inaczej, bo skoro jest 20 trójkątów, to mają w sumie 60 krawędzi, ale po dwie są wspólne.
Liczmy, ile piłeczek potrzeba. W każdym trójkącie jest tylko jedna kulka wewnętrzna - nie leżąca ani w wierzchołku naszej bryły, ani na krawędzi. Łącznie mamy zatem 20 takich kulek. Dochodzi 12 wierzchołkowych. Na każdą krawędź przypadają dwie kulki, które nie są wierzchołkowe (znajdują się wewnątrz krawędzi, ale nie wewnątrz ściany). Ponieważ jest 30 krawędzi, dawałoby to 60 kulek, ale po dwie są wspólne, czyli, że potrzeba ich tylko 30. Łącznie potrzeba zatem 20+12+30=62 kulek. Piłeczki można kupić po nie mniej niż 50 groszy za sztukę (zwykle jednak drożej). Jeśli doliczymy koszt kleju, wyjdzie… sporo. Ładne sklejenie wymaga kilku godzin uważnej pracy. Wszystko razem nadaje się na relaksujące zajęcie - polecam je zamiast np. oglądania telewizji.
Dygresja 1. W filmie-serialu Andrzeja Wajdy "Z biegiem lat, z biegiem dni" dwóch mężczyzn gra w szachy, "bo trzeba jakoś zabić czas przed obiadem". Rzecz dzieje się w galicyjskim Krakowie. Rzeczywiście: gazety już przeczytane (wtedy miały 4 strony), telewizji ani telefonu jeszcze nie wynaleziono, meczów piłkarskich nie ma. Nudy na pudy. W takiej sytuacji ludzie wymyślali sobie rozrywki. Dziś mamy je po naciśnięciu pilota…
Dygresja 2. Na zjeździe Stowarzyszenia Nauczycieli Matematyki w 2019 r. pewien hiszpański profesor demonstrował program komputerowy, który potrafił zamalować ściany brył na dowolne kolory. Było to z lekka upiorne, bo malowały same ręce, niemalże odcięte od tułowia. Pomyślałem sobie: ile przyjemności można mieć z takiego "zamalowania"? Wszystko trwa dwie minuty i w czwartej już nic nie pamiętamy. Tymczasem staroświeckie "robótki" uspokajają, kształcą. Kto nie wierzy, niech spróbuje.
Wracajmy do XXI wieku i naszych realiów. Jeśli nie chcemy relaksu w postaci mozolnego sklejania piłeczek, to choć narysujmy siatkę dwudziestościanu, którego krawędzie mają po cztery kulki. Jak to zrobić? Odpowiednio rozdrobnić rys. 6. Uważny Czytelnik domyśla się już zadania:
Zadanie 7. Czy można ponumerować piłeczki liczbami od 0 do 9 tak, by na każdej ścianie takiego dwudziestościanu występowały wszystkie te liczby?
Za co nam płacą?
Dzisiaj często stawiamy sobie pytanie o cel naszej działalności, a "szary podatnik" zapyta, dlaczego ma płacić matematykom za zajmowanie się takimi łamigłówkami?
Odpowiedź jest dość prosta. Takie "łamigłówki", same w sobie przecież interesujące, są "odpryskiem czegoś poważniejszego". Parady wojskowe to przecież jedynie zewnętrzna, widowiskowa część trudnej służby. Przytoczę tylko jeden przykład, ale zacznę od dziwnego, choć uznanego w świecie zagadnienia matematycznego. W 1852 r. pewien student angielski zapytał swojego profesora, czy każdą mapę można pokolorować czterema kolorami, tak by sąsiadujące państwa były zawsze przedstawione w różnych barwach? Dodam, że nie uważamy za "sąsiadując" te, które stykają się tylko w jednym punkcie, tak jak stany Wyoming i Utah w USA. Profesor nie wiedział… i problem czekał na rozwiązanie ponad sto lat.
Przyszło ono z nieoczekiwanej strony. W 1976 r. grupa matematyków amerykańskich napisała program, który miał to rozstrzygnąć (i rozstrzygnął: tak, zawsze cztery kolory wystarczą). Był to pierwszy dowód faktu matematycznego, osiągnięty za pomocą "maszyny matematycznej" - jak się pół wieku temu mówiło na komputer (a jeszcze wcześniej: "mózg elektronowy").
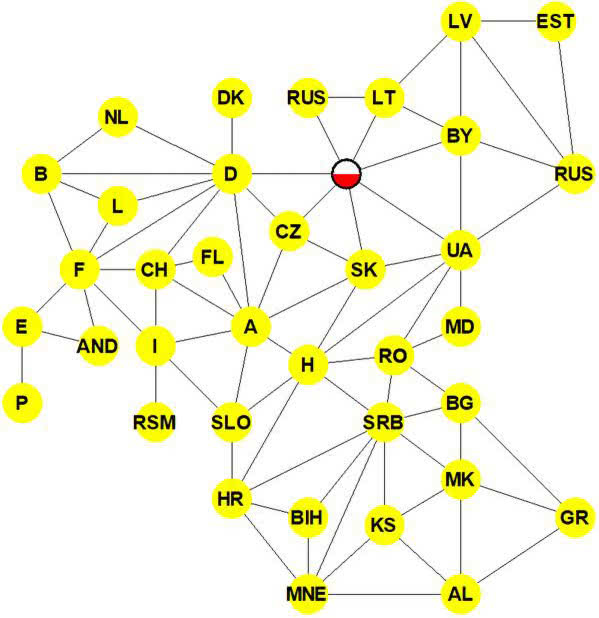
Oto specyficznie pokazana "mapa Europy" (rys. 9). Połączone są te kraje, które mają wspólną granicę. Pokolorowanie mapy jest tym samym, co pokolorowanie kółek owego wykresu (zwanego grafem) tak, by żadne połączone kółka nie miały tego samego koloru. Rzut oka na Lichtenstein, Belgię, Francję i Niemcy pokazuje, że trzy kolory nie wystarczą. Jeżeli chcesz, Czytelniku, pokoloruj czterema kolorami.
No tak, ale czy to też jest warte pieniędzy podatnika? Spójrzmy wobec tego na ten sam wykres nieco inaczej. Zapomnijmy, że są tam państwa i granice. Niech kółka symbolizują pakiety informacji, jakie mamy przesłać z jednego punktu do drugiego (np. z P do EST), a odcinki - to możliwe połączenia, z których każde ma swoją przepustowość. Jak najszybciej to przesłać?
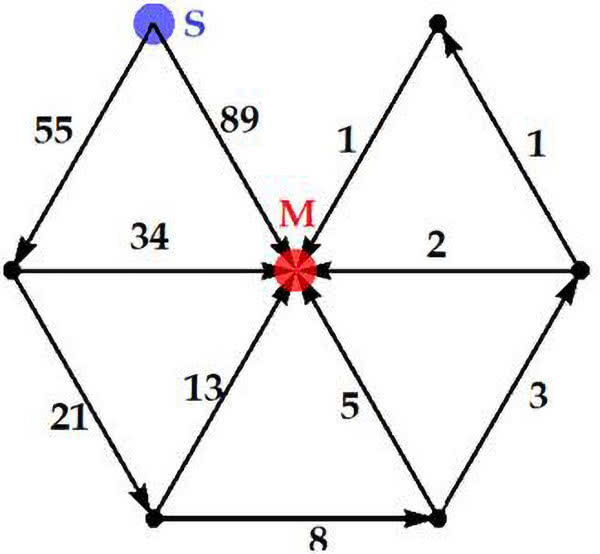
Zobaczmy najpierw bardzo uproszczoną, ale i bardzo interesującą matematycznie sytuację. Mamy coś przesłać z punktu S (= jak start) do punktu M (= meta), wykorzystując sieć połączeń o takiej samej przepustowości, powiedzmy 1. Widzimy to na rys. 10.
Wyobraźmy sobie, że chodzi o 89 bitów informacji, które mają trafić z S do M. Piszący te słowa lubi zadania o pociągach, zatem wyobraża sobie, że jest zawiadowcą w Stacyjce Zdrój, skąd ma skierować 144 wagony do stacji MegaPolis. Dlaczego akurat 144? Bo, jak zobaczymy, posłuży to do wyliczenia przepustowości całej sieci. Na każdym odcinku przepustowość jest równa 1, czyli w jednostce czasu może przejechać jeden wagon (jeden bit informacji, może być i Gigabite).
Zobaczmy, że wszystkie wagony spotykają się jednocześnie w M . Każdy dociera tam w 89 jednostek czasu. Jeżeli mam do wysłania bardzo ważny pakiet informacji z S do M, dzielę go na pęczki po 144 jednostki i pcham jak wyżej. Matematyka zapewnia, że tak jest najszybciej. Skąd wiedziałem, że trzeba 89? Tak naprawdę to zgadłem, ale gdybym nie zgadł, musiałbym rozwiązać układ równań Kirchhoffa (czy ktoś pamięta? - to równania opisujące przepływ prądu). Przepustowość sieci jest równa 184/89, czyli ok. 1,62.
O radości
Tak na marginesie, lubię liczbę 144. Lubiłem jeździć autobusem o tym numerze na plac Zamkowy w Warszawie - kiedy jeszcze nie było przy nim odbudowanego Zamku Królewskiego. Być może młodzi Czytelnicy wiedzą, co to jest tuzin. To 12 sztuk, ale tylko mocno starsi Czytelnicy pamiętają, że tuzin tuzinów, czyli właśnie 122=144, to tzw. gros. A wszyscy znający trochę więcej matematyki niż w programie szkolnym zorientują się od razu, że na rys. 10 mamy liczby Fibonacciego i że przepustowość sieci jest bliska "złotej liczbie"
W ciągu Fibonacciego 144 jest jedyną liczbą, będącą pełnym kwadratem. Sto czterdzieści cztery to również "liczba dająca radość". Tak właśnie hinduski matematyk-amator Dattathreya Ramachandra Kaprekar w roku 1955 nazwał liczby, które są podzielne przez sumę tworzących je cyfr:
Gdyby wiedział to Adam Mickiewicz, na pewno napisałby w "Dziadach" nie: "Z matki obcej; krew jego dawne bohatery/A imię jego czterdzieści i cztery", tylko zgrabniej: A imię jego sto czterdzieści cztery.
Rozrywka na poważnie
Mam nadzieję, że przekonałem Czytelników, iż łamigłówkowe zadania o sudoku to właśnie rozrywkowa strona zagadnień, które na pewno zasługują na poważne traktowanie. Nie mogę rozwinąć tego tematu szerzej. Aha, pełne obliczenie przepustowości sieci z diagramu widocznego na rys. 9 zajęłoby dwie, albo i więcej, godziny pisania układu równań - ewentualnie może nawet kilkadziesiąt sekund (!) pracy komputera.
Michał Szurek