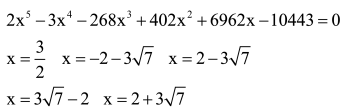Telefon komórkowy, XIX-wieczna kostka Rubika, trochę sudoku i algebra abstrakcyjna

Nie uczę już w szkole średniej, ale studentów, na ogół na ich pierwszym roku. Coraz częściej mówię do nich na zajęciach: "Wyjmujemy telefony…" Nie tylko dlatego, że mają tam kalkulatory i nie tylko dlatego, że mogą w Wikipedii znaleźć informacje, potrzebne im właśnie do rozwiązania zadania, ale i mogę za pomocą tej pralki, o, przepraszam, telefonu pokazać nawet niektóre zagadnienia algebry abstrakcyjnej. Mniej więcej o tym jest ten artykuł.
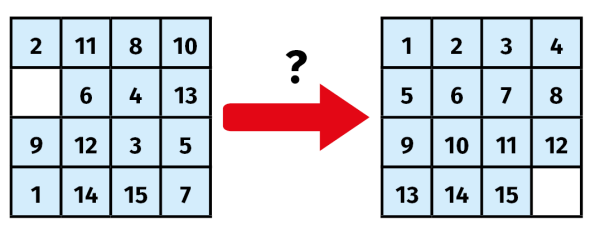
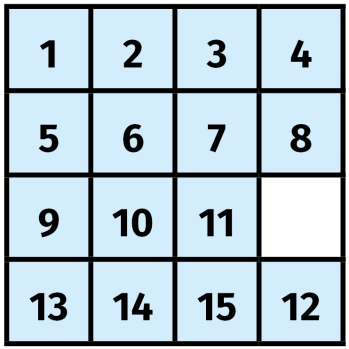
Zacznę od XIX wieku. Przez pewien, dość krótki zresztą, czas w intelektualnych kręgach była wtedy popularna gra w "piętnastkę". Można powiedzieć, że była to XIX-wieczna kostka Rubika. Można tę grę znaleźć i dzisiaj na Allegro. W kwadratowym obramowaniu mamy piętnaście przesuwalnych kwadracików, ustawionych na chybił trafił (matematyk powie: losowo). Zadanie polega na ułożeniu ich po kolei, w naturalnym porządku (1).
Gra jak gra - nie ma w niej strzelania, ucieczek, efektownej grafiki. Jest tylko trochę myślenia. Tysiące ludzi zmagały się sto pięćdziesiąt lat temu z jednym najtrudniejszym zadaniem (2). Liczby po lewej są ustawione "prawie" po kolei, tylko w ostatnim rzędzie mamy 13-15-14, zamiast 13-14-15. Jak może wiemy z pewnej reklamy telewizyjnej, "prawie" robi różnicę. Tak jest i tutaj.
W rozważaniach pomoże nam teoria grup. W 1826 roku, a więc prawie 200 lat temu Norweg Niels Henryk Abel rozwiązał problem, z którym bezskutecznie zmagali się uczeni włoscy XVI wieku: jak znaleźć ogólne wzory na rozwiązanie każdego równania piątego stopnia. Dziś może jesteśmy skłonni powiedzieć: a co za problem - wklepać dane do komputera i wyjdzie.
Na przykład:
Ale to nie tak. Dla tak prostego równania, jak x5-x-2=0 możemy tylko podać rozwiązanie przybliżone. Komputer wyliczy nam z dowolną dokładnością, na przykład, że
x≈1.26716830454212431725289142797768964122
ale dokładnego wzoru nie poda - bo go nie ma. Nie dlatego, że nie potrafimy znaleźć, bo równanie jest za trudne. Nie. Po prostu można wykazać, że takiego wzoru nie można podać. To z początku trudno zrozumieć, ale to ładnie obrazuje możliwości matematyki - nie są nieograniczone. Z drugiej jednak strony - matematyka ma monopol na dowody niemożliwości - że czegoś się nie da zrobić. Widziałem napisany około 1880 roku tekst, uzasadniający, że człowiek nigdy nie stanie na Księżycu. Dowód był prosty - nie ma tam atmosfery, zatem balonem się nie doleci. Wprawdzie od 49 lat rzeczywiście nikogo tam nie było, ale wiemy, że "gdyby nam się chciało", moglibyśmy znów tam dotrzeć.
Wrócę do matematyki. Niels Abel posłużył się pomysłem zabitego kilka lat wcześniej w pojedynku Evarysta Galois: z każdym równaniem zwiążemy pewną grupę i zbadamy własności tej grupy… Rezultat był nieoczekiwany. Są równania, dla których owa grupa jest tak zła, że wynika stąd, iż równania rozwiązać się nie da. Można oczywiście znaleźć rozwiązania przybliżone, ale dokładnych się nie da.
No tak, zdaję sobie sprawę, że nie wytłumaczyłem, co to jest grupa. W uproszczeniu można powiedzieć, że składa się ona z pewnych funkcji albo inaczej przekształceń, transformacji itp. Muszą one być do siebie jakoś "podobne" - ale bardziej precyzyjnie nie napiszę. Wystarczy taka intuicja. Może tylko kilka przykładów. Mamy grupę przesunięć (jej elementami są zatem przesunięcia w dowolnym kierunku), mamy grupę obrotów wokół jednego punktu o dowolny kąt. Mamy też grupę permutacji, czyli przestawianek.
Weźmy talię kart, fabrycznie opakowaną i ułożoną kolorami i wartościami, np. od dwójki do asa. Potasujmy. Otrzymamy permutację 52 elementów-kart. Tasowanie kart to poruszanie się w grupie permutacji.
Zrozumiałe jest zatem, że przesuwanie okienek naszej układanki to działania w grupie permutacji… szesnastu liczb. Dlaczego szesnastu, choć nawet w samej nazwie gry mamy 15? To jasne - wolne pole możemy traktować jako szesnasty element. Ono też przecież zmienia położenie.
Pomówimy teraz o inwersjach. Słowo to ma czasami miłą konotację. Z inwersją w górach mamy do czynienia, gdy zimne powietrze (zgodnie z prawami fizyki) spływa w doliny i często gęsto sprowadza chmury. Jest zimno, mokro i mgliście. Tymczasem na szczytach jest ciepło, słonecznie i mamy wspaniałą widoczność. Ale w matematyce "inwersja" oznacza raczej nieporządek. Zdarza się on, gdy większa liczba stoi przed mniejszą. Nie czeka grzecznie na swoją kolej, tylko spycha mniejszą do tyłu.
Na przykład w permutacji 1 4 3 2 mamy trzy inwersje, trzy nieporządki. Czwórka jest niezasłużenie przed trójką i przed dwójką a trójka przed dwójką. W ustawieniu "po kolei", np. 1 2 3 4 5 6 7 8, mamy zero inwersji, a gdy ustawimy osiem liczb "od końca": 8 7 6 5 4 3 2 1, będzie tych inwersji 7+6+5+4+3+2+1=28.
Pokolorujmy pola "piętnastki" na czarno i biało - w zwykłą szachownicę (3). Dołączmy wirtualny szesnasty element. W położeniu takim, jak na rysunku 3, "szesnastka" jest na białym polu, a permutacja nie ma inwersji. Matematycznie: ma zero inwersji.
Zero jest liczbą parzystą. Wspomnę tu swojego ojca, który wytłumaczył mi to kiedyś tak: jeżeli w misce jest zero pierogów, to można je sprawiedliwie podzielić na dwie albo więcej osób - każdy dostanie po tyle samo… po zero.
Inaczej mówiąc: permutacja 1 2 3…15 16 ma parzystą liczbę inwersji.
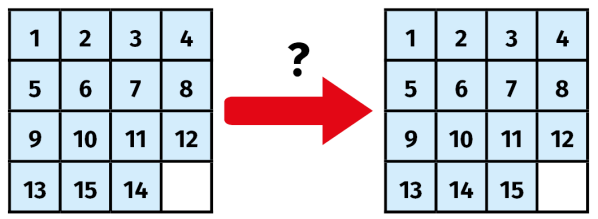
Mamy dwa typy ruchów: przesunięcie w poziomie i w pionie. Zanalizujmy je. Na rysunku 4 przesunąłem 15 na wolne pole. Pojawiło się ono wobec tego na lewo, w kwadraciku, który na naszej szachownicy z rysunku 3 jest czarny. Przypomnijmy sobie, że stoi tam "wirtualna" szesnastka. Widzimy zatem permutację
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 15.
Ile ma ona inwersji (nieporządków)? Tylko jedną (jeden) - szesnastka stoi przed 15. Liczba 1 jest nieparzysta.
Wprowadźmy trochę algebry. Będą dwie liczby, powiedzmy a oraz b. Każda z nich będzie albo równa +1, albo -1. Pierwszą z nich, czyli a, określimy tak: +1, gdy "szesnastka" jest na białym polu, a -1, gdy na czarnym. Druga b będzie jedynką (plus jedynką), gdy permutacja ma parzystą liczbę inwersji, a minus jedynką, gdy nieparzystą. Matematycy powiedzieliby, że rozpatrujemy sumę prostą dwóch grup multiplikatywnych: Z2 ⊕ Z2. Stąd cały pomysł - zaangażowanie teorii grup.
Położenie normalne to para (+1, +1). Po wykonaniu ruch "poziomego" (rysunek 4) zmienia się ona na (-1, -1), tj. a=1, b=1. Obie liczby zmieniają się. O właśnie: iloczyn ab pozostał równy +1.
Na rysunku 5 mamy ruch "pionowy" - przesunąłem 12 na wolne pole. Co się zmieniło? Wolne miejsce (=szesnastka) jest na czarnym polu, tzn. a=-1. Ile inwersji (nieporządków) mamy tam? Policzmy: szesnastka (=wolne pole) jest przed 13, 14, 15, 12 (cztery inwersje). Trzynastka, czternastka i piętnastka stoją przed dwunastką (trzy inwersje). Łącznie siedem, a to jest liczba nieparzysta, b=-1.
W porządku, iloczyn ab znów jest równy +1. Nietrudno zauważyć, że dla każdego ruchu będzie właśnie tak: iloczyn ab nie zmieni się. Matematycy powiedzieliby: dowolna transpozycja zmienia znak permutacji. Tak czy owak, do położenia "normalnego" można dojść tylko z tych pozycji, dla których ab=1. Jak wygląda sytuacja dla konfiguracji, w której 15 zamieniła się z 14 (6)? Wolne pole jest na miejscu białym (a = +1), ale permutacja ma tylko jedną inwersję (15-14), a zatem b=-1, iloczynem jest niestety -1. Trudno zresztą określić, czy niestety, czy "stety". Z układu z rysunku 6 nie da się dojść do położenia normalnego bez inwersji.
Zobaczmy, co z położeniem z rysunku 1. Wolny kwadracik jest na polu, które zaznaczyliśmy na czarno, zatem a=-1. Pracowicie licząc inwersje, naliczymy ich 59, a zatem b=-1. Iloczyn wyniesie +1. Konfiguracja jest "ustawialna", można z niej dojść do naturalnej…
Uważny Czytelnik odkryje błąd logiczny. Wykazaliśmy tylko, że z pewnych układów nie da się dojść do podstawowego. Jest ich zresztą połowa wszystkich możliwych. Skąd wiadomo, że nie ma jeszcze innych ograniczeń?
Istotnie, tego fragmentu rozumowania nie ma. Gdy pobawimy się grą, stanie się jasne, że warunek ab=+1 jest również wystarczający.
Ile jest zatem możliwych konfiguracji, jakie można otrzymać z podstawowej? Jeżeli pamiętamy, że 16 liczb można ustawić na 16!=20922789888000 sposobów. Połowę z nich da się ustawić. To daje 10461394944000. Popuśćmy wodze fantazji.
Wyobraźmy sobie, że układamy kolejne konfiguracje, po jednej na sekundę. Pracujemy bez snu i jedzenia 24 godziny na dobę. No, pozwólmy sobie na odpoczynek każdego 29 lutego. Ile czasu zajmie nam ułożenie wszystkich? Nietrudno obliczyć: trochę ponad 331728 lat. Kawał czasu. Ale gdyby do roboty zaprząc całą ludzkość, nawet bez małych dzieci, chorych, niesprawnych - powiedzmy 3 miliardy. Uporaliby się w niespełna godzinę. To obliczenie ma jeden sens: pokazuje, jak wiele jest nas na jedynej planecie, która jeszcze nas lubi. Bo w kolonizację Marsa jakoś nie wierzę.
Kostka Rubika przeżyła szczyt swojej popularności 40 lat temu. Uczyłem wtedy w warszawskim XIV Liceum imienia Klementa Gottwalda, komunistycznego prezydenta Czechosłowacji. Po 1990 roku Liceum wróciło do przedwojennego patrona, Stanisława Staszica. Ciekawe, czym naraził się Staszic rządom PRL…Ale nie będę w to wnikał. Jeszcze mam w uszach skrzypienie dziesiątek prekręcanych na przerwach (i lekcjach!), jakie rozlegało się w szkołach całej Polski w trudnym okresie wiosną 1982 roku.
Kręcono nimi na lekcjach i przerwach, w tramwaju, na ulicy, w czasie meczu i na wycieczkach. Tamta "pandemia" była nieszkodliwa, choć Douglas R. Hofstadter opisał taką oto jednostkę chorobową:
Cubitis magikia. Poważny rozstrój umysłowy, połączony z jednoczesnym swędzeniem końców palców. Ulgę przynosi jedynie dłuższy kontakt z wielobarwną kostką pochodzenia węgierskiego i japońskiego. Objawy często nie zanikają przez wiele miesięcy. Wysoce zaraźliwe!
Jak wiele wynalazków, tak i ten nie wziął się znikąd. Na przełomie XIX i XX wieku wśród dziecięcych skarbów w domach angielskich znajdowało się niekiedy "pudełko Mac Mahona" - zawierało drewniane sześcienne klocki, pomalowane na sześć kolorów. Należało zrobić to, co z kostką Rubika; ułożyć sześcian o jednokolorowych ścianach.
Chcę jednak omówić trudniejszą (niż piętnastka, ale oczywiście nieporównanie łatwiejszą niż kostka Rubika) i matematycznie ciekawszą grę, którą miałem właśnie na swojej pierwszej komórce. Była to zresztą Nokia 3210. Wykorzystuję tę grę, gdy uczę studentów algebry.
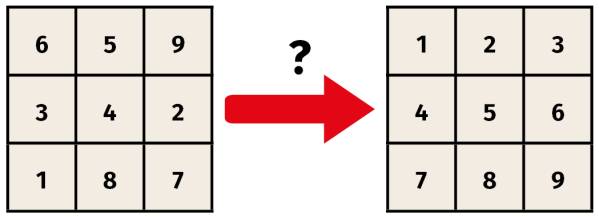
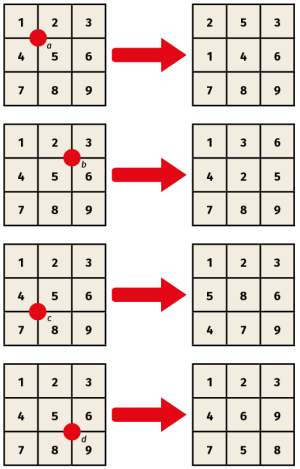
Na ekranie ukazuje się dziewięć liczb, ustawionych w kwadrat, na przykład jak na rysunku 7. Można wykonywać następujące działania, oznaczę je przez a, b, c, d (8). Każde z nich to obrót małego kwadracika 2×2 w kierunku przeciwnym do wskazówek zegara. Oczywiście obrót w drugą stronę, przeciwną uzyskujemy przez trzykrotny obrót w pierwszą.
Pytanie jest oczywiście jak poprzednio: czy każdy układ można przywrócić do wyjściowego położenia 1 2 3 4 5 6 7 8 9 za pomocą operacji a, b, c, d.
Nie będę szczegółowo opisywał, jak udało mi się rozstrzygnąć ten problem przy wykorzystaniu prostej teorii grup. Powiem tylko, że sądzę, iż podobne, choć tysiąckrotnie bardziej złożone rozumowanie musieli przeprowadzić polscy kryptografowie Marian Rejewski, Henryk Zygalski i Jerzy Różycki, którzy złamali niemiecki szyfr Enigma podczas wojny.
W teorii grup ważną rolę grają komutatory. To wyrażenia postaci xyx-1y-1, albo i dłuższe:
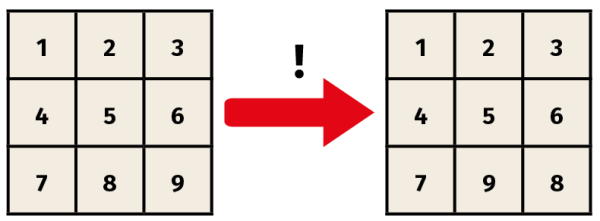
xyztux-1y-1z-1t-1u-1. W Centrum Nowych Technologii Uniwersytetu Warszawskiego, na marmurowej tablicy poświęconej matematyce, mamy fragment obliczeń Rejewskiego, Zygalskiego i Różyckiego: właśnie takie długie komutatory. A my przyjrzyjmy się komutatorowi b-1 c b c-1 . Wykonajmy te operacje po kolei i dostawmy na końcu czwarty obrót, ale w drugą stronę, czyli b-1 c b c-1 d-1. Otrzymamy wynik na rysunku 9.
Bingo! Widzimy, że udało się przestawić dwie sąsiednie liczby: 8-9 zamienić na 9-8. To już droga do celu; trzeba trochę pokombinować, żeby móc przestawić dowolne dwie liczby, a to znaczy, że "wszystko można". Każdy układ da się doprowadzić do początkowego! Z przytoczonych rozważań można też wydostać algorytm: jak doprowadzić dane ustawienie do położenia normalnego, ale to już byłoby za dużo matematyki. Powiem tylko, że matematyk od razu zapyta o podobną grę w większym kwadracie albo prostokącie i o stosowny algorytm, a wszystko to mieści się w zagadnieniu najszybszego sortowania dużych plików. To zagadnienie o żywotnym znaczeniu dla całej informatyki - a w XXI wieku informatyka dotyka każdego.
Gdy zaczynałem pisać ten artykuł, chciałem dojść i do sudoku - bo i na tym przykładzie można pokazać duży fragment abstrakcyjnej matematyki. No, to mam temat na następny odcinek…
Michał Szurek