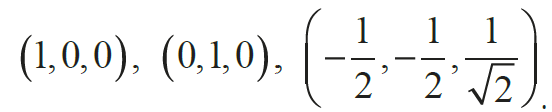Najwyższa nagroda matematyczna dla Ukrainki
Medal Fieldsa jest najwyższym wyróżnieniem dla matematyka i traktowany jest jako odpowiednik Nagrody Nobla. Może nawet jest czymś więcej, bo przyznaje się go raz na cztery lata - choć na ogół dla kilku (dwóch do czterech) osób. Wyboru dokonuje oczywiście odpowiedni komitet, złożony z uczonych o najwyższej renomie. W odróżnieniu od Nagrody Nobla, preferowani są ludzi młodzi, poniżej 40. roku życia. Jest smutną prawdą, że czterdziestoparoletni matematyk ma już swoje najlepsze lata za sobą; wyjątki są nieliczne. W naukach humanistycznych czterdziestka to dopiero początek rozwoju - bo tu gra dużą rolę dojrzałość społeczna i doświadczenie życiowe.
Ustanowienie takiego wyróżnienia zasugerował w swoim testamencie kanadyjski matematyk John Charles Fields (1863-1932). Był wystarczająco dobrze sytuowany, by ufundować zarówno medal, jak i związaną z nim nagrodę pieniężną 15000 dolarów kanadyjskich. Dziewięćdziesiąt lat temu była to przyzwoita suma. Sam medal wykonany jest z 14K złota; ma kształt koła o średnicy 63,5 mm, waży 169 gramów. Z jednej strony jest na nim głowa Archimedesa i cytat z rzymskiego poety, astrologa i filozofa stoickiego Marcusa Maniliusa (I wiek n.e.) - transire suum pectus mundoque potiri (Wznieść się ponad granice ludzkich możliwości i przewodzić światu), z drugiej - napis Congregati ex toto orbe mathematici ab scripta insignia tribuere (Zebrani z całego świata matematycy honorują wielkie osiągnięcia).
Wartość samego medalu jest szacowana na 5500 CND (dolarów kanadyjskich) - ale oczywiście trudno sobie wyobrazić, by laureat/ka chciał/a medal sprzedać. Przecież jeśli chodzi o pieniądze, to ma "jak w banku" zapewnioną posadę w najlepszych uniwersytetach świata. Może, jak piłkarz Robert Lewandowski, przebierać w ofertach. To chyba jasne.
Medale są przyznawane na kongresach Międzynarodowej Unii Matematycznej, odbywających się raz na 4 lata. Był jeden wyjątek: na 1982 rok zaplanowano kongres w Polsce, ale z powodu stanu wojennego u nas przełożono go na 1983. Kongres 2022 zaplanowany był w mieście, które przez większą część mojego życia było Leningradem, teraz nazywa się inaczej. W związku z napaścią Rosji na Ukrainę kongres przeniesiono do przestrzeni wirtualnej, ale uroczystość wręczenia medali odbyła się już na żywo w Helsinkach.
Maryna Wiazowśka jest drugą kobietą w historii, uhonorowaną tym odznaczeniem. Pierwszą była Iranka Maryam Mirzakhani (2014). Nim skupię się na odkryciach Laureatki, wymienię trzech pozostałych - przecież to też matematycy z najwyższej półki: Brytyjczyk James Maynard z Oksfordu, June Huh (Korea → USA, Princeton University) i Hugo Duminil-Copin (Francja, Institut des Hautes Études Scientifiques).
Nie jest łatwo opowiedzieć przystępnie o tych odkryciach - jak zresztą i o większości odkryć matematycznych najwyższego szczebla. Najpierw powiem tak, pewnie nie całkiem zrozumiale (można opuścić ten akapit): prace Wiazowśkiej łączą teorię algebr Liego, reprezentacji podgrup skończonych w grupie izometrii przestrzeni euklidesowych, analizę Fouriera, a wszystko w sosie modnej od półwiecza geometrii algebraicznej. Dotyczą diagramów Dynkina - struktur pojawiających się jak Deus ex machina w najrozmaitszych działach matematyki. Najwięksi matematycy próbowali to ogarnąć, zrozumieć, czemu diagramy te pojawiają się nieoczekiwanie tu i tam. Przypomina mi się motyw z jednego z opowiadań Stanisława Lema. Występował tam smok, pojawiający się jednocześnie w wielu miejscach. Lem tłumaczył: gdy wystawimy dłoń spod wody, niewprawny obserwator zobaczy pięć oddzielnych palców, a dopiero po dłuższych rozważaniach może dojść do wniosku, że jest to pięć palców jednej ręki. Zawsze wzbudzał we mnie strach koncept "myślącego oceanu" (Solaris). Dlaczego Lem nie dostał Nobla? Trudno pojąć.
Ale jednak spróbuję przybliżyć Czytelnikom jeden z wątków odkryć Laureatki. Można powiedzieć, że właśnie "odkryła smoka", tego z Lema.
W młodości grywałem w koszykówkę, dość zresztą nieźle. Pamiętam, jak po treningu trener pakował piłki do worka. Do dużego worka wchodziło zaledwie kilka. Nic dziwnego; okrągłe źle się mieści w przestrzeni. Jak źle? Jak można najlepiej? Zacznijmy od kół na płaskiej powierzchni. Polecam eksperyment, coraz trudniejszy do wykonania z powodu… inflacji i coraz powszechniejszego użycia kart płatniczych. Coraz trudniej o monety, zwłaszcza o małych nominałach. Ale może uda nam się zgromadzić kilkanaście jednakowych. Połóżmy je na stole i dopychajmy do siebie. Zobaczymy, że będą "same" dążyć do trójkątnej piramidki, jak na rysunku 1. Zamiast monet możemy wziąć - jak na fotografii 2 - rzodkiewki. Z pomidorami raczej nie próbować! Można obliczyć, że koła zajmują około 89% pola. To łatwe szkolne zadanie. Układ ten widzimy też na rysunku 6.
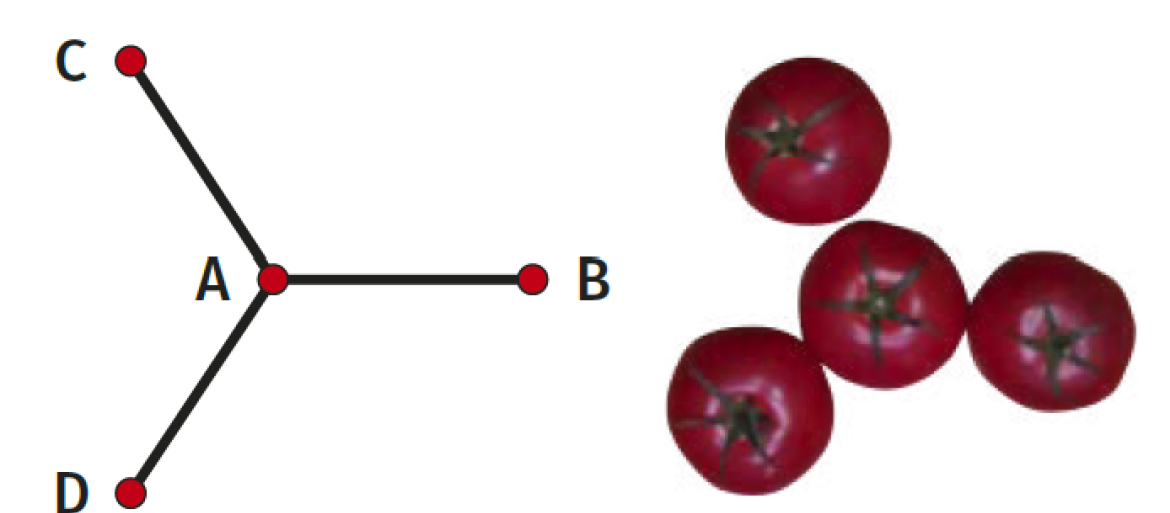
Co z kulami w przestrzeni? Intuicja podpowiada nam, że najlepsze upakowanie to też takie w piramidkę - tyle że czworościenną. Układamy pierwszą warstwę tak, jak rzodkiewki na rysunku 2, a następne (jabłka, rzodkiewki, pomarańcze, a na fotografii 3 grapefruity) wkładamy w zagłębienia pierwszej warstwy i tak dalej. Osiągamy gęstość nieco mniej niż 75% - to już trudniejsze, ale wciąż szkolne zadanie. Ciekawe, że tę samą gęstość osiągamy nieco innym sposobem. Na fotografii 4 widzimy bryłę sklejoną z piłeczek pingpongowych. Takie bryły pasują jedna do drugiej i możemy wypełniać nimi całą przestrzeń - oczywiście nie ściśle, tylko z dziurami. Obliczenie, ile miejsca tracimy, jest zadaniem na poziomie dobrego maturzysty; oczywiście rozwiązanie można też sobie gdzieś wygooglować.
Ale czy na pewno jest to najlepsze upakowanie? Otóż to! Takie pytanie postawił w 1611 roku Johannes Kepler, bardziej znany ze swoich odkryć astronomicznych. Na rozwiązanie czekaliśmy stosunkowo niedługo, 387 lat. Dopiero w 1998 roku Thomas Callister Hales ogłosił dowód, który jednak - zdaniem specjalistów - był tylko "poprawny na 99%” - a to z powodu trudności z prześledzeniem algorytmów komputerowych, użytych w dowodzie. Hales wziął się do pracy i po 16 latach (czyli w roku 2014) podał dowód, który został już zaakceptowany.
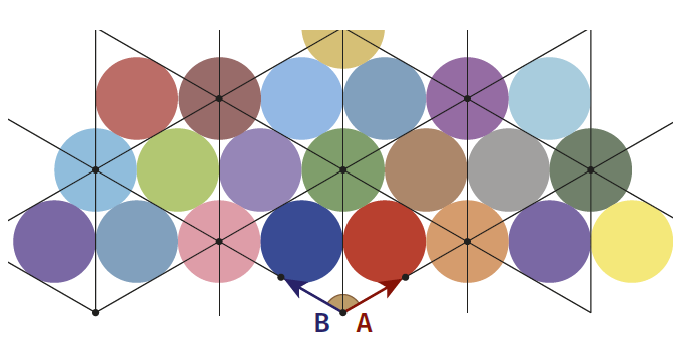
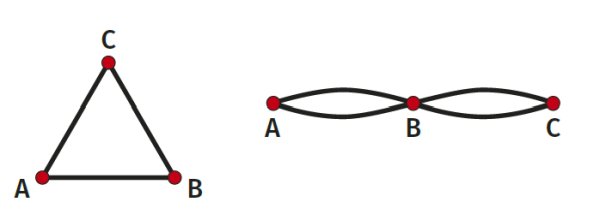
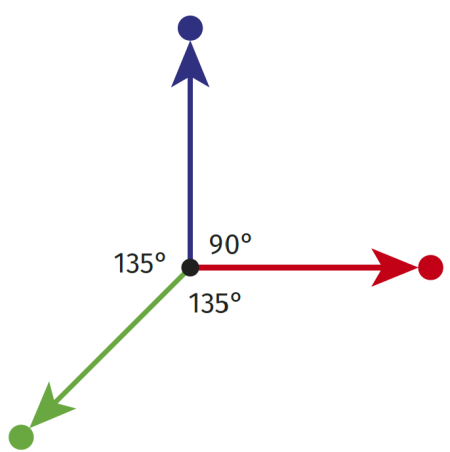
Wejdę teraz w matematykę na poziomie uniwersyteckim. Naprawdę - choć będzie się można zdziwić, że to "takie proste". Spójrzmy na rysunki 5, 8 i 11 - mamy na nich punkty (kropki) połączone odcinkami. To swoisty sposób kodowania położenia wektorów w przestrzeni. Konwencja jest prosta: każdy punkt to wektor (po prostu strzałka). Jeżeli punkty są połączone jedną kreską, to znaczy, że odpowiadające im wektory tworzą kąt 120°, dwie kreski symbolizują kąt 135°, a trzy - 150°. Dlaczego takie kąty? Są to wielokrotności 30° i 45° - podstawowych kątów sieci krystalicznych.
Jeżeli punkty nie są połączone, to znaczy, że odpowiadające im wektory są prostopadłe (90°). Popatrzmy zatem na rysunku 5 - dwa albo trzy punkty na jednym odcinku. Pierwszy układ to dwa wektory nachylone do siebie wzajemnie pod kątem 120°. Widzimy je na rysunku 6 - dwa skromne wektory A, B tworzą bazę całej sieci trójkątnej i realizują układ monet z fotografii 1 i rzodkiewek z fotografii 2.
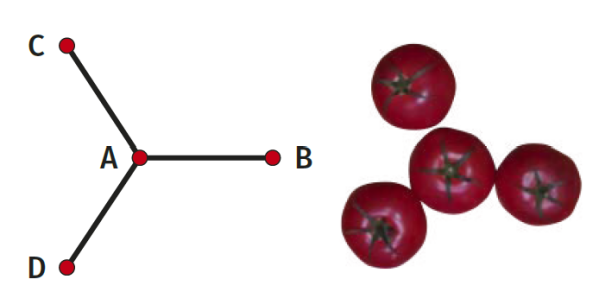
Diagram A3 tworzy bardziej skomplikowany układ, choć wciąż nietrudny do "ogarnięcia". Wektory A i C są prostopadłe, a B tworzy z nimi kąt 120°. To się da utworzyć w przestrzeni trójwymiarowej; należy wziąć wektory o współrzędnych:
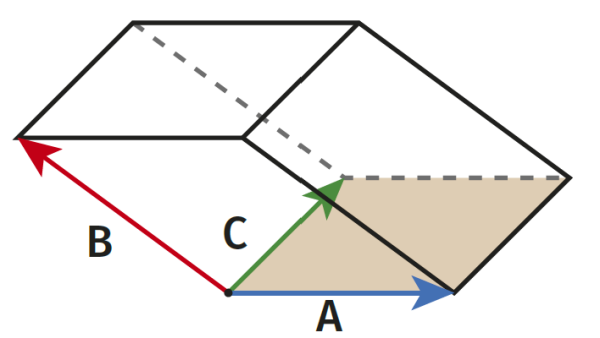
Łatwo je sobie wyobrazić jako krawędzie "przewracającego się" graniastosłupa (rysunek 7). Wektory A, B są prostopadłe, wektor C tworzy z nimi kąty po 120°.
Zadanie (szkolne). Pod jakim kątem wektor B jest nachylony do płaszczyzny podstawy graniastosłupa?
Tu muszę wygłosić ważną uwagę, skierowaną do kolegów i koleżanek matematyków/matematyczek, którzy mogą skrytykować, że to trochę nie tak". Jak widzicie, nie chcę tu mówić o systemach pierwiastków, tylko o bazach, a i to upraszczając. Albert Einstein: wszystko należy upraszczać, jak tylko można, ale nie bardziej!
Zróbmy kilka ćwiczeń. Bez większego trudu zrozumiemy, co daje trójkąt ABC z rysunku 8. Trzy wektory, tworzące każdy z każdym kąt 120°. Jedyna możliwość to… logo Mercedesa - trzy wektory rozmieszczone równomiernie. Druga część rysunku 8 daje układ, gdzie wektor A jest prostopadły do C, natomiast B tworzy z nimi oboma kąt 135°, czyli tak, jak na rysunku 10.
Ćwiczenie. Jak zakodować układ trzech krawędzi sześcianu wychodzących ze wspólnego wierzchołka?
Odpowiedź: Trzy kropki, niepołączone w ogóle odcinkami!
Przechodzimy do trudniejszego zadania (rysunek 11). Co skrywa diagram Dynkina, tradycyjnie oznaczany symbolem D4?
Przyjrzyjmy się. Mamy mieć trzy wektory wzajemnie prostopadłe (bo punkty B, C, D nie są połączone), natomiast czwarty, A, tworzy z każdym z nich kąt 120°. Tego nie da się osiągnąć w przestrzeni trójwymiarowej, musimy wejść w czwarty. Jeżeli ktoś z czytelników zna podstawy geometrii analitycznej, łatwo zgodzi się, że mogą to być wektory.
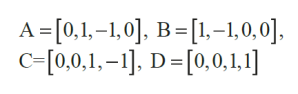
To już trudno narysować.
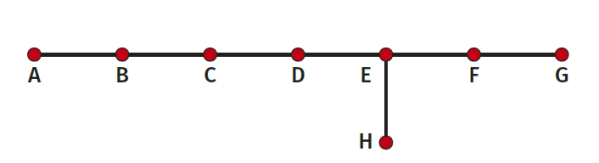
Przeskoczę kilkanaście pięter matematyki, do diagramu o oznaczeniu E8 (rysunek 12). Pamiętamy zasady - kodujemy układ ośmiu wektorów, tworzących kąty: między AB, BC, CD, DE, EF, FG i IH jest po 120°, a pozostałe pary są prostopadłe. Realizacja takiego układu to już przestrzeń ośmiowymiarowa. Znalezienie takich wektorów jest dość trudnym (ale nie przesadnie trudnym) zadaniem na poziomie pierwszego, może drugiego roku studiów - oczywiście na takich kierunkach, gdzie matematyka nie jest traktowana po macoszemu. Dla porządku podam te wektory, ale to nie jest istotne (można oczywiście przeskoczyć te cyferki):
[2, –2, 0, 0, 0, 0, 0, 0], [0, 2, –2, 0, 0, 0, 0, 0], [0, 0, 2, –2, 0, 0, 0, 0],[0, 0, 0, 2, –2, 0, 0, 0], [0, 0, 0, 0, 2, –2, 0, 0], [0, 0, 0, 0, 0, 2, –2, 0],[0, 0, 0, 0, 0, 0, 2, –2], [–1, –1, –1, –1, –1, 1, 1, 1].
Od tego już niedaleko do odkrycia Wiazowśkiej, a w każdym razie do zrozumienia, o co w tym chodzi. Zmieniając trochę te wektory, dochodzimy do takiego układu (tym razem trzeba współrzędne wektorów czytać pionowo, z góry na dół). Z nich powstaje cała sieć (podobnie jak z dwóch wektorów A, B na rysunku 6). W węzłach tej sieci umieszczamy kule o promieniach. Otrzymujemy upakowanie o gęstości 384 0, 25387. Najgęściej upakowane kule w przestrzeni ośmiowymiarowej zajmują niewiele ponad 25% przestrzeni. Już w 1935 roku Hans Frederic Blichfeld wykazał, że jest najlepsze upakowanie dla tak zwanych pokryć kratowych (regularnych). Dla dowolnych konfiguracji jest to zadanie bardziej złożone - o kilka(naście) pięter trudności. Na ich pokonaniu polegają odkrycia Halesa i Wiazowśkiej, przy czym o metodzie Laureatki mówi się, że jest zdumiewająco prosta i piękna.
Wstaw kule w wierzchołki sieci, która z tego powstaje, a otrzymasz najgęstsze upakowanie
jednakowych kul w przestrzeni wymiaru 8
Czytelnik może poczuć się rozczarowany. I to wszystko? Nie, nie wszystko. Ale można pytać dalej: jaką wartość ma ten wynik, jak wpływa na nasze codzienne życie? Czy to tylko jakaś igraszka matematyków? Czy ktoś płaci za takie rozważania, a jeśli to idzie z naszych podatków, to dlaczego mamy je przeznaczać na to właśnie?
Zacznę od końca. Uczeni, trochę podobnie jak wojsko i lekarze, są również potrzebni "na wszelki wypadek". Gdybyśmy mieli zagwarantowane zdrowie i bezpieczeństwo, można by się obejść bez doktorów i żołnierzy. Dalej, jeśli nawet dla nas najważniejszy jest lekarz domowy, to przecież zgadzamy się, że badania naukowe w medycynie są konieczne. Postępy informatyki wlokłyby się w ślimaczym tempie, gdyby nie matematyka. Zgadzamy się dotować teatry, popieramy artystów, choć moglibyśmy się bez nich obejść. Jeżeli zaś chodzi o czystą matematykę, to wartość odkryć Wiazowśkiej polega po pierwsze na postępach w zagadnieniach, które były nierozwiązane przez blisko 400 lat. Po drugie - ale to już trzeba wejść w samą matematykę - na powiązaniu z pozoru odległych faktów, twierdzeń i teorii. To piękny fragment matematyki. Dla wirtuoza, choć może nie dla fantasty. Z dużym wzruszeniem przekopywałem się przez prace Laureatki - do pełnego zrozumienia bardzo, ale to bardzo mi daleko.
Historia uczy, że najdziwniejsze odkrycia matematyczne mogą znaleźć zastosowanie. Przez stulecia teoria liczb uchodziła za ciekawą dyscyplinę, nazywaną nawet Królową Matematyki - ale o zastosowaniach mowy nie było. Ot, intelektualne figle. Mniej więcej pół wieku temu okazało się, że to potrzebne i to do nie byle czego: do kodowania i szyfrowania, w tym na przykład do podpisu elektronicznego. Och, wcale nie pół wieku temu. Wojnę 1920 roku wygraliśmy również dzięki matematykom, którym udało się złamać szyfry wojsk rosyjskich, a kto rozszyfrował niemiecką Enigmę w czasie II wojny? Matematycy! Problemy dotyczące najlepszego upakowania sfer mają zastosowanie w "error correcting code", co można przetłumaczyć jako "algorytm poprawiania błędów" (w domyśle: w przekazywaniu wiadomości w sieci).
Wracając do Maryny Wiazowśkiej, przypomnę Stanisława Lema: chodzi o odkrycie smoka. Dobrze, żeby okazał się dobrotliwy.
I jeszcze jedno. Profesor Wiazowśka dopiero na samym końcu wykładu powiedziała kilka słów o obecnej (połowa lipca) sytuacji. Pokazała zdjęcia z ogródka swojej mamy, spod Kijowa (fotografia 14). Wojska rosyjskie były o 5 km od jej domu. Teraz jest spokojnie (powiedziała Laureatka) i dodała: chciałabym każdemu Polakowi i każdej Polce móc wręczyć taki bukiet kwiatów za Waszą pomoc. Napisałem na czacie: sława Ukrainie, herojam sława.
Michał Szurek