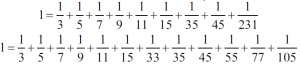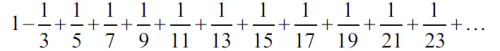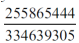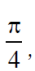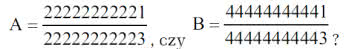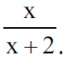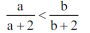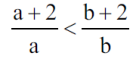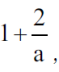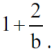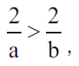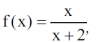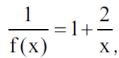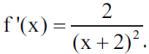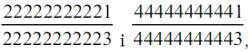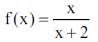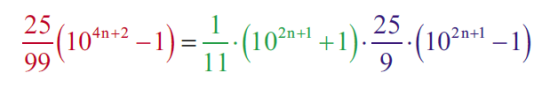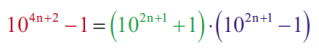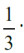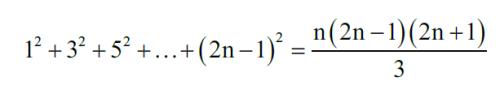Jeszcze o liczbach nieparzystych

W naszych czasach bardziej nam się podobają liczby parzyste - są  takie równe. Oddaje to angielska nazwa: even numbers, podczas gdy nieparzyste są "dziwne": odd numbers. W języku, którym mówi się w tym kraju za Ukrainą (nazwy tego kraju nie wymienię), mamy parzysty = четный, czyli jakby "honorowy", co z kolei wiąże się ze staropolskimi określeniami "cetno" i "licho". Możemy się uśmiechnąć, że w pierwszej polskiej książce matematycznej (1538, autorstwa księdza Tomasza Kłosa) mamy zwrot "przyszło w licho", co znaczy "otrzymaliśmy liczbę nieparzystą".

Nieparzystość jest niekiedy pożądana. Komisje i komitety powinny się składać z nieparzystej liczby członków - bo inaczej mogą być kłopoty z podjęciem decyzji, gdy jest remis. Na ogół zresztą przyjmuje się wtedy, że decyduje głos przewodniczącego.

Nieznajomość elementarnej matematyki może i tu doprowadzić do nieporozumień. Przyjmuje się niekiedy, że "bezwzględna większość" to 50% plus jeden głos. Przyjrzyjmy się. Jeżeli komisja ma 7 osób, to 50% plus jeden arytmetycznie równa się cztery i pół; ale nie można mieć "cztery i pół głosu" poparcia. Tak więc z dosłownego rozumienia tej zasady wynikałoby, że  "bezwzględna większość" to co najmniej 5:2. Niewiele brakowało, a wskutek tej zasady Wojciech Jaruzelski nie zostałby prezydentem w 1989 r.

Czy pamiętamy, że liczby pierwsze są nieparzyste: 3, 5, 7, 11, 13, 17, 19, 23, 29 i tak dalej? Jeśli tak pamiętamy ze szkoły, to… źle pamiętamy. Liczba 2 też jest pierwsza: dzieli się przecież tylko przez 1 i siebie. Przypomnę również, że liczby 1 nie zaliczamy ani do pierwszych, ani do złożonych. Dla starożytnych Greków jedynka w ogóle nie była liczbą, bo - mówiąc dzisiejszym językiem - nie opisywała liczności żadnego zbioru. Dzisiaj matematycy mówią, że należy odróżnić zbiór jednoelementowy od tego elementu. Tłumaczyłem to uczniom tak: jeżeli w pewnej małej, wiejskiej szkole w klasie jest trzech uczniów, a odejdzie dwóch, to klasa będzie miała tylko jednego ucznia, ale będzie to oddzielna klasa, z dziennikiem i wychowawcą.

Programowania uczyłem się oczywiście w mocno dojrzałym wieku. Przedtem … nie było co programować. Dotknąłem po raz pierwszy klawiatury komputera, gdy miałem 40 lat. Nie, nie 4, tylko 40. To robi różnicę. Pamiętam, że jednym z pierwszych programów, jakie napisałem, dotyczył algorytmu na rozkład liczby 1 na sumę ułamków o liczniku 1 i nieparzystym mianowniku. Przypuszczamy, że taka suma musi się składać z co najmniej dziewięciu ułamków i musi być w niej mianownik co najmniej równy 105.

Pół wieku temu samo sprawdzenie, że tak jest, mogło wpędzić uczniów (i nie tylko ich) w roztrój nerwowy. Pisemne dodawanie ułamków było i jest umiejętnością obcą znacznej części nawet licealistów. Przekonuję się o tym stale.

Rodzice uczniów (bardziej niż sami uczniowie) zapytają: jaki sens mają takie zadania? Odpowiedź jest prosta: to takie trochę SUDOKU matematyczne. Z tym, że bardziej matematyka niż łamigłówka. Natomiast samo napisanie programu jest dobrym ćwiczeniem dla początkujących informatyków (w każdym razie tych, którzy będą pisać programy, a nie tylko znać się na gotowych aplikacjach).

Skoro mowa o ułamkach, to jeszcze gorzej idą uczniom obliczenia z ułamkami piętrowymi. A ja zawsze je lubiłem. Tak ładnie wyglądają… Oto ciekawe

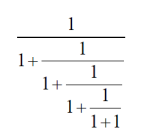
Zadanie 1

Oblicz:

Jaki będzie wynik, gdy dopiszemy jeszcze kilka(naście) kresek ułamkowych?
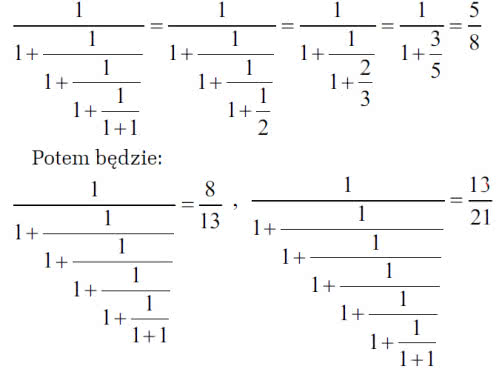
Spróbujmy:

i tak dalej

Tak to znaczy jak? W licznikach i mianownikach pojawiać się będą wyrazy ciągu Fibonacciego: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, … Jak może pamiętamy, każdy wyraz tego ciągu jest sumą dwóch poprzednich. Za  moich studenckich czasów mawialiśmy, że każdy obiad w stołówce stu-denckiej jest także sumą dwóch poprzednich!

Ciąg Fibonacciego odnajdujemy w wielu miejscach matematyki użytkowej, nawet w matematycznej analizie giełdy - chociaż wydaje mi się to wpychaniem metod matematycznych na siłę tam, gdzie są mało przydatne Gottfried Wilhelm Leibniz (1646–1716) jest znany jako matematyk, choć bardziej niż nim, był jednak filozofem. I ja odejdę zatem na chwilę od matematyki. Od  zawsze nurtowało nas wszystkich, dlaczego na świecie jest tyle zła. Leibniz odpowiedział na to w niesamowity sposób. Rozumowanie jego może się wydać nieco przewrotne. Otóż, mówi Leibniz, Pan Bóg stworzył najdoskonalszy świat, jaki może istnieć. Nie mógł stworzyć innego świata, bo wtedy sam nie byłby doskonały. A zatem świat, w  którym byłoby mniej zła, byłby gorszy. Zła jest tyle, ile powinno być.

Hm. Niech i tak będzie. Wolę się skupić na podziwianiu tak zwanego szeregu Leibniza. Będę na przemian dodawał i  odejmował odwrotności kolejnych liczb nieparzystych:

Do czego dojdę? Obliczmy sumę, którą właśnie napisałem. Otrzymamy ułamek:

Czy to naprawdę jest coś ciekawego? Nie, niespecjalnie. Obliczmy wartość dziesiętną tego ułamka i pomnóżmy przez 4. Wyjdzie, też w przybliżeniu, 3,0584. Co może być interesującego w tej liczbie? Tak naprawdę to nic. W każdym razie niewiele. Ale - i to jest właśnie odkrycie Leibniza - kolejne sumy będą się zbliżać do 

jednej czwartej znanej wszystkim, tajemniczej liczby π.

Pamiętam, że przeżyłem swego rodzaju dreszcz emocjonalny. Pitagorejczycy mówili, że liczby rządzą światem. I to nie dlatego, że za ich pomocą można zapisywać stan kont bankowych wszelkich oligarchów. Liczby Pitagorasa rządziły światem w sposób metafizyczny, tworzyły wszystko.

W szeregu Leibniza piszę, dodaję i odejmuję najprostsze liczby - dochodząc do owej niewymiernej i niealgebraicznej liczby wiążącej zakrzywiony obwód koła z jego średnicą. Dzisiaj już mi to odkrycie spowszedniało, ale w wieku 20 lat przeżywa się wszystko silniej. I jeszcze ciekawostka. W 1984 roku kupiłem sobie w Kanadzie programowany kalkulator. Dopuszczał pętle złożone z co najwyżej sześciu instrukcji. Udało mi się zaprogramować go tak, by obliczał kolejne sumy szeregu. Zostawiłem go na całą noc. Wstałem przed świtem. Nacisnąłem Enter. Zgadzało się. Liczba pi była równa 3,1415…

Szereg Leibniza dąży do swojej granicy bardzo powoli. Trzeba blisko tysiąca wyrazów, by otrzymać znane nam wszystkim przybliżenie π≈3,14. Szereg taki nie nadaje się do bezpośrednich obliczeń. Trzeba wziąć inne szybko zbieżne szeregi.

Wróćmy do ułamków. Często daję studentom takie.

Zadanie 2

Która liczba jest większa?

Mówię, że chodzi tu o rozwiązanie zadania bez elektronicznych urządzeń liczących. Co więcej, że jest to zadanie do rozwiązania w pamięci, bez obliczeń.

Rozpiszę się na temat tego zadania. Najpierw jednak zaprzęgnijmy do pracy matematykę. Zdarza się i nawet dość często, że łatwiej jest rozwiązać zadanie ogólniejsze niż podane szczegółowe. Można powiedzieć, że z oddali lepiej widzimy. Użyjmy więc algebry. Zauważmy, że obydwa ułamki są postaci

Dla liczby A mamy x= 22222222221, dla liczby B jest x=44444444441. Wykażę, że jeżeli 0<a<b, to:

Ta ostatnia nierówność jest równoważna nierówności odwrotnej na odwrotnościach, czyli:

Ale lewa strona tej ostatniej nierówności to

prawa to 

Czyli zgadza się: jeżeli a<b, to

a zatem dla wyjściowej funkcji musi być odwrotnie… Może za  dużo tego "odwracania kota ogonem", ale to jedyna trudność.

Dla maturzystów: można to ująć inaczej, zgrabniej, używając funkcji. Przyjrzyjmy się funkcji 

w dziedzinie liczb dodatnich x. Czy jest ona rosnąca, czy malejąca? Jest rosnąca wtedy i tylko wtedy, gdy jej odwrotność jest malejąca. Odwrotność tej funkcji to 

a to jest oczywiście malejąca - bo przecież gdy mianownik rośnie, to ułamek maleje, a zatem nasza wyjściowa funkcja jest rosnąca.

I jeszcze wytoczę "armatę na wróbla". Nasza funkcja f(x) jest ciągła i różniczkowalna. Obliczam pochodną tej funkcji, zgodnie z regułą różniczkowania ilorazu. Otrzymuję

Pochodna jest dodatnia, a zatem funkcja jest rosnąca.

W zadaniu było polecenie, żeby rozwiązać je bez "elektroniki", ale zobaczmy, co ona daje. Aby porównać ułamki

jemy mnożenia krzyżowe 22222222221·44444444443 i  22222222223·44444444441. Wyniki nie mieszczą się w  okienkach żadnego kalkulatora, a nawet są za duże dla Excela. Skorzystałem z ogólnie dostępnego programu Wolfram-Alpha. Dał on: 22222222221·44444444443=987654320901234567903 22222222223·44444444441=987654320945679012343

Drugi iloczyn jest większy, a więc drugi ułamek jest większy.

Rys. 1

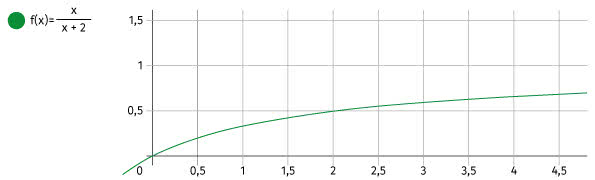
Mimo wszystko sprawdźmy. Zróbmy wykres funkcji (1): 

Zgadza się, funkcja jest rosnąca. Coraz wolniej, ale idzie do góry.

To jeszcze nie koniec analizy rozwiązania o skomplikowanych ułamkach. Staram się wpajać uczniom, żeby w miarę możliwości sprawdzali rozwiązanie ze zdrowym rozsądkiem. Największe "osiągnięcie" miał na tym polu pewien student geografii, któremu wyszło z obliczeń, że biegun północny jest 114  km od Warszawy. Co gorsza, nie widział w tym żadnej niedorzeczności. "Tak podał kalkulator, o proszę".

I oto rozwiązanie czysto rozumowe, bez żadnych rachunków. Spójrzmy na nasze ułamki. W obydwu różnica między mianownikiem a licznikiem jest taka sama, równa 2. Powiedzmy, że są to dwie jakieś jednostki. Im większe liczby, tym różnica ta ma mniejsze znaczenie, a zatem drugi ułamek musi być bliższy jedynki niż pierwszy.

***

Zadanie 3

A oto ładna piramidka liczbowa: 

25=1·25252525=91·2775
2525252525=9091·277775
25252525252525=909091·27777775
252525252525252525=90909091·2777777775
2525252525252525252525=9090909091·277777777775

Jaka jest reguła jej budowy? Napisz stosowny wzór. 

Zadanie 4

Uporządkuj od najmniejszej do największej liczby:

Zadanie 5

Zbuduj z klocków ładną wieżę, w której piętra będą kwadratami, których długości boków są  kolejnymi liczbami nieparzystymi. Oblicz kubaturę takiej wieży złożonej z sześciu pięter.

Zadanie 6

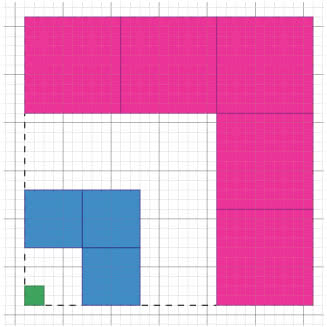
Spójrz na  rysunek 2. Czy widzisz na nim sumę 1³+3³+5³?

Rys. 2

Rozwiązanie zadania 3

Oto ta zależność:

Dowód jest bardzo łatwy. Polecam maturzystom wykonanie stosownych rachunków, a mianowicie: współczynnik liczbowe po obydwu stronach to 

a wzór skróconego mnożenia (na różnicę kwadratów) daje równość:

Rozwiązanie zadania 4

Nie do wiary, ale te wszystkie liczby są równe! Wystarczy sprawdzić. Można przeprowadzić ciekawy ogólny dowód formalny. Też warto prześledzić. W liczniku jest suma n początkowych liczb nieparzystych; wiemy, że ta suma to n². W mianowniku
mamy dalszych n liczb, razem więc 2n. Suma kolejnych 2n liczb nieparzystych to (2n)²=4n². W mianowniku jest różnica sumy 2n początkowych liczb nieparzystych i n takich liczb, czyli wartość mianownika to 4n²–n²=3n². Po skróceniu ułamka
otrzymujemy 

Rozwiązanie zadania 5 

Kubatura takiej wieży to 112+92+72+52+32+12. Udowodnienie ogólnego, ładnie wyglądającego wzoru na sumę kwadratów kolejnych liczb naturalnych to znów ćwiczenie dla maturzystów:

Komentarz do zadania 6

Ja… widzę tę sumę. Kolejne zaś zadanie dla uczniów: udowodnić wzór na sumę sześcianów kolejnych liczb nieparzystych. Wygląda przystępniej niż suma kwadratów:

1³+3³+5³+...+(2n–1)³=n²(2n²–1) 

Michał Szurek