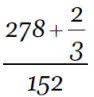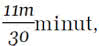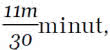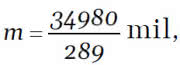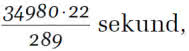Cudowne, z lekka bezsensowne zadania

Kilka następnych zadań pochodzi od Lewisa Carolla, autora Alicji w Krainie Czarów. Lewis Carroll był matematykiem, znanym także ze swoich abstrakcyjno-nonsensownych idei. Doradzał na przykład posługiwanie się mapami w skali 1:1 i sugerował zmianę oznaczeń sin i cos na… jakieś dziwne. W 1891 roku opublikował niewielką książeczkę Problemy do poduszki. Zawierała ona 72 zadania matematyczne, które rozwiązywał, gdy nie mógł spać. Już pierwsze zadanie… może nas nieźle uśpić. Ale spróbujmy przetrzymać ogarniającą nas senność.
Zadanie 1. Gdy 1 lipca mój zegar ścienny wybił godzinę ósmą, na zegarku kieszonkowym była 8.04. Poszedłem na spacer do Greenwich i gdy w obserwatorium biło południe, mój zegarek pokazał 5.59. Dnia 30 lipca o godzinie 9 rano według zegara ściennego, zegarek ręczny pokazywał 8.57, a tego samego dnia w południe według zegarka ręcznego, na zegarze w Greenwich była już 12.05. Tego dnia o jedenastej wieczorem obydwa zegary (ręczny i ścienny) pokazały tę samą godzinę. Jaką godzinę pokażą zegary w prawdziwe południe (tj. GMT) 31 lipca?
Zadanie to przepisałem z… własnych notatek sprzed wielu lat. Zacząłem rozwiązywać i… doszedłem do wniosku, że właśnie w tej wersji jest to tzw. bardzo dobre zadanie. Treść może i nudnawa, ale…
Rozwiązanie jest ciekawsze od samego zadania. Przeczytajmy kilka razy. Widać, że "coś jest nie tak". Pierwsze podejrzenie budzi godzina 5.59, gdy obserwatorium Greenwich podaje południe. Po drugie, jeżeli przez dwadzieścia dziewięć dni (od 1 do 30 lipca) były tak niewielkie różnice między zegarami, cóż może zajść w jeden dzień? Po trzecie: pierwszego lipca rano zegarek ścienny spieszy się względem ściennego cztery minuty, 30 lipca rano późni się trzy minuty a potem od razu wyrównują się. Co u licha?
Mamy do czynienia nie tylko z zadaniem matematycznym, ale i łamigłówką: "co się przeinaczyło przy kolejnych kopiowaniach tekstu? Nie umiem już dojść, czy błąd był w oryginalnej książce, czy w moich notatkach, kilkakrotnie przepisywanych. I to właśnie jest właściwe zadanie: jak było naprawdę? Jakie zadanie chciał ułożyć autor?
Na kursach, gdzie uczy się redaktorów książek, egzamin polega między innymi na zredagowaniu tekstu: przeczytania tekstu, wyłapania błędów i chropowatości. Jeżeli na przykład autor napisał, że benzyna była w powszechnym użyciu od końca XVIII wieku, redaktor "musi" to zauważyć i poprawić na "XIX". Jeżeli napisze, że ci mali Murzyni należą do plemienia Masajów, redaktor musi poprawić na "Pigmejów" - Masajowie to właśnie plemię bardzo wysokie. I tak dalej.
Może i to jest pomysł na nauczanie "inne niż zwykle". Nie "trzy z": zakuj, zdaj, zapomnij, tylko "trzy p": przeczytaj, pomyśl, popraw.
Wróćmy do zadania z zegarami. Nietrudno zgodzić się z tym, że tak zwany chochlik drukarski zamienił 11.59 na 5.59. Co z 30 lipca? Postawmy roboczą hipotezę: autorowi zadania chodziło o trzeci lipca, nie trzydziesty. Zero zostało "gdzieś, kiedyś" dopisane. Sprawdźmy tę hipotezę.
Kryptolodzy mawiali, że każdy szyfr da się złamać, każda zakodowana informacja da się odczytać - pod warunkiem że otrzymany tekst jest rzeczywiście komunikatem, że zawiera jakąś treść. Dzisiaj znamy szyfry, dla których prawdopodobieństwo złamania w czasie, powiedzmy, kilku lat (!) jest bliskie zeru, ale jeśli chodzi o proste kodowanie, pogląd kryptologów jest prawdziwy. Opisuje to z emocją Stanisław Lem (Głos Pana).
Załóżmy więc, że Lewis Carroll ułożył dobre, nie-złośliwe zadanie. Mamy tylko je zrekonstruować, jak archeolog wazę ze skorupek.
I może to jest pomysł…, może i to wplatać w lekcje matematyki? Nie chwal się, że znasz algorytm. Najpierw odkryj, wysupłaj, wyjaw sens. Rozwiązać zadanie… to byle komputer potrafi. Ale znaleźć sens? Wytropić, "co autor miał na myśli".
No, to do pracy. Przeróbmy 5.59 na 11.59, bo to wynika z kontekstu. Przetestujmy hipotezę, że "30 lipca", powinno być "3 lipca". Pierwszego lipca o ósmej rano zegarek ręczny wyprzedzał ścienny o cztery minuty, a 49 godzin później (3 lipca o dziewiątej) spóźniał się o trzy minuty. To nie może być przypadek, czujemy, że jesteśmy na właściwym szlaku, jak na odnalezionym z powrotem szlaku w górach. A zatem dalej pracujemy przy założeniu, że ręczny spóźnia się względem ściennego o minutę na siedem godzin. Dość dużo, ale w XIX wieku nie było elektroniki, jaka dzisiaj oplątała cały świat.
Następny kłopot czeka nas 3 lipca wieczorem. Zegarek ręczny jakoś dziwnie przyspieszył. Analizujemy tekst: "w południe według zegarka ręcznego, na zegarze w Greenwich była już 12.05". Zarówno Sherlock Holmes, jak i nawet Hercules Poirot (jak pamiętamy, był Belgiem) pomyślałby wtedy: co robi człowiek, który stwierdza, że jego zegarek późni się aż o pięć minut w stosunku do czasu, którym żyje całe Imperium? To proste. Człowiek ten ustawia zegarek na właściwy czas - popycha zegarek o pięć minut. Minuty sprzed dwóch dni nie uwzględnił. Tego nie było w treści zadania - to musieliśmy sami wyciągnąć z analizy tekstu. To dlatego o jedenastej wieczorem 3 lipca ścienny zrównał się z ręcznym: rano "sam z siebie" opóźniał się o trzy minuty, do wieczora opóźnił się jeszcze o dwie (bo upłynęło dwa razy po siedem godzin), no, ale w południe dostał "doping" pięciominutowy.
Teraz już prosto… Z początkowych danych wynika, że ręczny spóźnia się według Greenwich o 4 minuty na 48 godzin, a więc dwie minuty na dobę. 3 lipca w południe były nastawione tak samo. Zatem 31 lipca, po dwudziestu ośmiu dobach, zegarek ręczny wskaże 11.04… o ile nie będziemy go regulować, a to sugeruje zadanie. Co wskaże ścienny - pozostawiamy Czytelnikowi z komentarzem, że na pewno tak kiepskich zegarków nie było w wiktoriańskiej Anglii… Chyba że wymyślimy inną interpretację zadania.
Zadanie 2 (też Lewis Carroll). Podróżni A i B idą tą samą drogą w tym samym kierunku, maszerując codziennie od 6 rano do 6 wieczorem. W poniedziałki A przechodzi 10 mil, we wtorki 9 mil, w środy 8 mil i tak dalej aż do soboty, gdy przechodzi 5 mil. Podróżny B zaczyna od 2 mil w poniedziałek, następnie we wtorek przebywa 4 mile, w środę sześć, w czwartek osiem, piątek dziesięć, w sobotę dwanaście. W niedzielę odpoczywają. Pewnego poniedziałku rano (o godz. 6) B wyprzedzał A o 14 mil. Zakładając, że idą jednostajnym krokiem, wyliczyć, gdzie i kiedy się spotkają.
Komentarz: zadanie jest urocze (co docenimy, rozwiązując) i bawi nierealnym doborem danych. Lewis Carroll mało liczył się z realiami. Na przykład w poniedziałek podróżny B szedł 12 godzin jednostajnym krokiem i przeszedł dwie mile. Mila na sześć godzin to dwieście kilkadziesiąt metrów na godzinę… metrów, nie kilometrów! 12 mil w sobotę to też niewygórowane wymagania: 3 kilometry na godzinę, co prawda jednostajnie i bez przystanku...
Teraz rozwiązanie. Zauważmy, że tygodniowo A przebywał 10+9+8+7+6+5=45 mil, a B tylko 2+4+6+8+10+12=42, a zatem A nadrabiał 3 mile na tydzień. W poniedziałek wieczorem A był już tylko 6 mil za B. We wtorek wieczorem tylko milę. Co się działo w środę? Do godziny 12 piechur A przeszedł połowę dziennego dystansu, czyli 4 mile, a podróżny też połowę swojej środowej porcji, czyli 3 mile. Wtedy się spotkali.
Ale co było dalej? Do końca dnia A nadrobił milę i tak wystartowali w czwartek rano. Czwartkowa porcja dla A to 7 mil, dla B osiem. A zatem czwartkowy wieczór znów ich połączył. Z treści zadania wynika, że A wypił więcej piwa niż B, bo w piątek wlókł się (6 mil przez cały dzień), podczas gdy B "machnął" dziesięć. Nadrobił cztery, a w sobotę dołożył jeszcze siedem. Niedzielny ranek zastał ich odległych o 11 mil, a więc przez tydzień A nadrobił trzy mile…i powtarzamy obliczenia. Wynik: podróżny A doganiał B w środę w południe, w czwartek na samym końcu dnia, następnie we wtorek w drugim tygodniu
o 15.34, w kolejny poniedziałek o 18.00 (na końcu dnia) i po raz ostatni w piątek ok. 12.26.
***
Bardziej jako ciekawostkę i żeby "ocalić od zapomnienia" niż do poważnej analizy przytaczam dwa zadania o pociągach z ponad 100-letniego zbiorku Stanisława Michalskiego Nowy zbiór przykładów i zadań algebraicznych, wraz z teorją, wyd. M. Arcta, Warszawa–Poznań–Lwów–Równe–Lublin–Łódź–Wilno. Zbiorek był w użyciu jeszcze przed odzyskaniem niepodległości przez Polskę; mój egzemplarz, wyraźnie przeredagowany (wydanie czwarte), pochodzi z 1922 roku. Autor pisze, że zastosował się do wytycznych Ministerstwa z dnia 18 lipca 1921 roku. Zbiorek kupiłem za złotówkę w sklepie ze złomem (!) w Kazimierzu w 2004 roku. Aha, nie wiem, czy Czytelnicy wiedzą, że nie zrealizowałem chłopięcych marzeń: chciałem być konduktorem kolejowym, a zostałem profesorem matematyki. Nie wszystkie plany udaje nam się zrealizować. Ale oto zadanie:
Zadanie 3. O godzinie 8.40 wyszedł z Warszawy pociąg pospieszny do Poznania via Toruń. O tej samej godzinie wyruszył z Poznania balon sterowy typu "Zeppelin" i poszybował w kierunku Warszawy, lecąc stale ponad torem kolejowym również via Toruń. Szybkość pociągu pospiesznego 72 km, a balonu sterowego 80 km na godzinę. Pociąg stracił wskutek postoju na stacjach 1 godzinę 16 minut, natomiast balon szybował bez przerwy z jednakową szybkością. Odległość pomiędzy Warszawą a Poznaniem wynosi 380 kilometrów. W ile godzin po wzlocie balon znajdzie się nad parowozem pociągu pospiesznego?
Zadanie też urocze, również ze względu na wątki pozamatematyczne. Narzuca się pytanie: dlaczego pociąg pospieszny z Warszawy do Poznania jechał przez Toruń, a nie wprost, przez Konin, Koło i Swarzędz? Z oczywistej przyczyny: w XIX wieku z Warszawy do Poznania jechało się koleją kaliską albo właśnie przez Toruń. Obie trasy były międzynarodowe. Dopiero w 1921 roku wybudowano linię z Konina do Poznania przez Strzałkowo, co było najkrótszym połączeniem Warszawy z Poznaniem. Nawet dzisiaj, kiedy wyjeżdżam z Poznania pociągiem w kierunku Warszawy, mam wrażenie, że jest to odgałęzienie od linii głównej na Toruń. Zbiorek, z którego biorę zadanie, został napisany kilka lat wcześniej i nie był poprawiany. A czy wszyscy wiedzą, co to był "balon sterowy typu Zeppelin"?
Zadanie ma też niejasną treść. Nie wiadomo, kiedy pociąg stracił ową godzinę i 16 minut. Przyjmijmy, że przed spotkaniem z balonem. Możemy więc założyć, że wyjechał już z Warszawy z tym opóźnieniem. Byłaby wtedy godzina 9.56. Do tego czasu balon przeleciał 101 1/3 kilometra. I teraz już prosto: dzieliło ich 278 2/3 kilometra przy szybkości względnej 152 km na godzinę. Trzeba podzielić:
…ojojoj, jakie to trudne… równa się, o, jak prosto wychodzi:
godziny; to znaczy godzina i 50 minut. Teraz też nie jest łatwo: jeżeli od 9.56 upłynęła godzina pięćdziesiąt minut, to która jest? Oczywiście trzeba dodać dwie godziny do 9.56 (będzie 11.56) i odjąć dziesięć minut. Jedenasta czterdzieści sześć.
No, to ja dam Czytelnikowi zadanie, na mój ulubiony temat: ułóż zadanie. Zmień jak najmniej treść zadania wyjściowego, by balon nadleciał nad parowóz punktualnie o godzinie 12.00. Możesz oczywiście przesunąć wszystko o te 14 minut. Ale może manipuluj prędkościami i opóźnieniem pociągu?
Zadanie 4. (Michalski, 1922). W poniedziałek o godzinie 12-ej w południe podług czasu miejscowego z miasta A wychodzi pociąg pospieszny, przebywający po 6 mil na godzinę i dąży w kierunku miasta B, leżącego na zachód od A na tymże równoleżniku. Pociąg przybywa do B w czwartek o godzinie 7 minut 26 rano czasu miejscowego (B). Jaka jest odległość między miastami A i B, jeżeli pociąg nie zatrzymuje się na przystankach i co mila, wskutek biegu w kierunku zachodnim, zyskuje 22 sekundy?
Zadanie jest bardzo ciekawe zupełnie niezależnie od swojej niebanalnej treści matematycznej. Daje odskocznię do innych problemów, pozwala wczuć się w nie tak dawną przeszłość. Zastanówmy się najpierw nad znaczeniem słów "zyskuje 22 sekundy". Przyjmujemy, że znaczy to, że co milę czas lokalny zmienia się o 22 sekundy. Gdy nie było nawet słowa "globalizacja", a podróże trwały długo, regiony miały swój własny czas, niezwiązany z przynależnością do stref czasowych. Na przykład przewodnik Walerego Eljasza po Tatrach z 1891 roku podawał rozkład jazdy pociągiem do Tatr z komentarzem: "daty podane są według czasu krakowskiego; czas lwowski różni się od tego o 16 minut". Czas na terenie całej Polski ujednolicono dopiero po odzyskaniu niepodległości. Zadanie to jest najwyraźniej reliktem z wcześniejszej edycji zbiorku... i dobrze, że się zachowało. Jak i w wielu innych cytowanych przeze mnie zadaniach, ich autor mało dba o realia. Nasz pociąg jechał około 19 godzin bez przerwy.
O jakiej mili może być mowa w zadaniu? Były wtedy (pod koniec XIX wieku) na ziemi polskiej trzy mile: geograficzna=7,426 km, austriacka=7,586 km i polska=8,536 km. Najbardziej prawdopodobna (również ze względu na rozwiązanie) jest mila geograficzna.
Rozwiązujmy. Przyjmijmy, że maszynista nie przestawiał zegarka. Która godzina była na jego zegarku, gdy po tak długiej podróży dotarł do celu? Trzeba do 7,26 dodać
gdzie m jest liczbą przebytych mil. Dlaczego dodać? Wyobraź sobie, że lecisz samolotem do Anglii, gdzie czas jest o godzinę wcześniejszy…
A więc pociąg był w drodze 19 godzin 26 minut +
Lepiej przeliczyć to na minuty: 1166 +
Prędkość 6 mil na godzinę to jedna dziesiąta mili na minutę. Droga to prędkość razy czas; a zatem
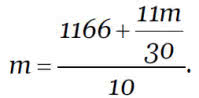
Wyznaczamy stąd
czyli nieco ponad 121 mil, ok. 900 km.
Nasuwa się kilka komentarzy. Dzisiaj tak się nie układa zadań - uczeń jest przyzwyczajony, że odpowiedź nie powinna być "dzika". Można dyskutować z tym poglądem, bo przecież w zadaniach "z życia" na ogół nie ma okrągłych liczb. Po drugie, sprawdźmy jednak rozwiązanie z realiami geograficznymi. Pociąg "zyskał"
to jest blisko trzy czwarte godziny. Zakładamy, że rzecz się dzieje w naszych szerokościach geograficznych. Długość równoleżnika krakowskiego to około 40 000 km razy cos(50°), czyli około 25700 km (dlaczego? - a, to osobne zadanie!), czyli 900 km odpowiada w przybliżeniu 50 minutom różnicy w czasie lokalnym. Zadanie było zgodne z realiami!
Wykorzystajmy też cytowaną informację z przewodnika Walerego Eljasza, że "czas krakowski różni się od lwowskiego o 16 minut" do obliczenia odległości między tymi dwoma niegdysiejszymi stolicami Galicji. Skoro 900 km odpowiadało 50 minutom, to 16 minut daje (jak to obliczyć?) około 288 km. A jak jest w rzeczywistości? Możesz sprawdzić? Jak? No wiesz, takie pytanie w XXI wieku?
I na zakończenie jeszcze dwa zadania. Pierwsze znów o pociągach.
Zadanie 5 (Michalski, 1922). Pociąg osobowy idzie z A przez B do C (przypuszczamy, że B i C leżą na prawo od A), zatrzymując się w B siedem minut. W 2 minuty po wyjściu z B pociąg ten spotyka inny pociąg pospieszny, idący na jego spotkanie z 2 razy większą szybkością. Pociąg pospieszny wyszedł ze stacji C w chwili, gdy osobowy znajdował się o 28 km na lewo od B. Wiemy, że pociąg pospieszny przebywa przestrzeń pomiędzy C i B w ciągu 1½ godziny; następnie, gdyby pociąg ten po przybyciu do A i nie zatrzymując się na tej stacji, natychmiast wyruszył z powrotem, to przybyłby do C w 3 minuty po przybyciu do tej stacji osobowego pociągu. Ile kilometrów robi na godzinę każdy pociąg i jaka jest odległość pomiędzy A, B i C?
Wielu z Czytelników pomyśli sobie: "a cóż to za głupie zadanie - nic dziwnego, że matematyka to ogłupianie ludzi za pomocą cyferek!" Każdy nauczyciel matematyki musi odpowiadać na pytanie: "Po co mam to robić - przecież to mi się w życiu nie przyda!". Różnie na to odpowiadamy, ale niekiedy trafia do uczniów porównanie, że to po prostu trening intelektualny. Jeżeli nie potrafisz pomyśleć nad takim zadaniem, to może nie jesteś tak dobry intelektualnie, jak mi się zdawało? A sportowcy też robią na treningu ćwiczenia, których potem nie ma na meczu…
Rozwiązania nie podam.
Drugie zadanie pochodzi podobno z college'u w Cambridge, z… 1815 roku - jakże jest ono nieekologiczne. Dziś już nie strzela się do zwierząt dla rozrywki. Wiem, że tacy ludzie są i dziwię się temu.
I tu nie podam rozwiązania, nie chcąc zabierać Czytelnikom przyjemności myślenia nad tym cudownie bezsensownym zadaniem.
Zadanie 6. Dwaj myśliwi przynieśli z polowania 10 ptaków. Suma kwadratów liczb strzałów, jakie oddał każdy z nich, wyniosła 2880, iloczyn zaś tych samych liczb był 48 razy większy od iloczynu liczby ptaków, jakie ustrzelił każdy z nich. Gdyby B oddał tyle strzałów co A, to ustrzeliłby 5 razy więcej ptaków niż A. Ile ptaków zabił każdy z nich?
***
Jedna rzecz od razu się narzuca. Pan A był kiepskim myśliwym. A co do zadania - cóż, taka była wtedy matematyka. Można się pośmiać z tych zadań, ale myślenia na pewno uczyły. Zresztą, naukę języków obcych traktowano też jako ćwiczenia umysłowe. Bo i kto 200 lat temu podróżował? Garstka arystokratów.
Michał Szurek