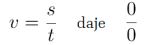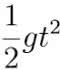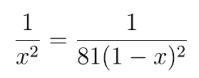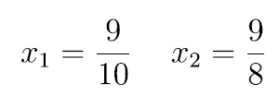Punkty charakterystyczne

Otóż w listopadzie dostałem egzemplarz prestiżowego czasopisma „Nature” z 2022 roku z opisem odkrycia drugiego Trojańczyka naszej planety. Szczerze mówiąc, zrozumiałem z niego tylko geometrię i kilka danych liczbowych, dotyczących orbity i przypuszczalnego składu chemicznego planetoidy. Przypomniałem sobie jednak, jak o tym (to znaczy o punktach libracyjnych, z potwierdzonym w 1906 roku odkryciem planetoidy w takim punkcie dla układu Słońce-Jowisz) opowiadał nam na wykładzie fizyk, profesor Andrzej Jurewicz, zmarły w 2013 roku.

Ale ponieważ jesteśmy w kąciku „Rozmaitości Matematyczne”, więc najpierw będzie stosunkowo dużo o prostej geometrii elementarnej - z elementami filozofii włącznie.

W geometrii wszystko składa się z punktów. Nie mamy trudności ze zrozumieniem, czym jest punkt - chociaż z logicznego punktu widzenia jest z tym trochę dziwnie. Punkt nie ma rozmiarów - ani długości, ani szerokości, ani oczywiście wysokości. Wyobrażamy go sobie jako małą kropkę albo kulkę w przestrzeni. Jest jednak mniejszy od kropki, która kończy to zdanie. Jest nawet od niej nieskończenie razy mniejszy. Zatem skąd to nasze wyobrażenie, że jest kółeczkiem albo kulką? Może dlatego, że koło i kula - może raczej okrąg i sfera - są dla naszych zmysłów idealnymi figurami geometrycznymi. Są „wszędzie takie same”. Wobec tego także idealny punkt powinien być okrągły. Takie rozważania nie mają jednak znaczenia. Punkt to punkt… i kropka.

Swoim zwyczajem skręcę i w obszar odległy od matematyki. Mamy w potocznym języku kilka określeń, związanych z punktem. Przedstawić coś w kilku punktach to znaczy wypunktować. Ten ostatni czasownik ma inne znaczenie na przykład w boksie (=wygrać na punkty).

Jeśli mamy w planie poważną dyskusję, warto przyjść na nią punktualnie. Gdy znajdziemy najbardziej istotną część rozumowania albo planu działania, możemy powiedzieć, że z naszą analizą trafiliśmy w punkt, a gdy przekonam oponenta do mojego punktu widzenia, to „punkt dla mnie”.  Potem dalsze sprawy będziemy omawiać punkt  po punkcie. Przy ważnych kwestiach możemy powiedzieć, że to dla mnie punkt honoru. Przeciwnik może to zbyć lekceważącym: „no cóż, punkt widzenia zależy od punktu siedzenia”. Może też być przewrażliwiony na jakimś punkcie.

W końcu dyskusja może dojść do punktu kulminacyjnego. Może to być punkt krytyczny, ale jeżeli wszyscy chcą się dogadać, będzie to punkt zwrotny. Stanie się punktem wyjścia do spisania porozumienia.

Jak wszyscy wiemy, punkty mamy i w wielu dyscyplinach sportowych. Oto zadanie dla Czytelnika-kibica: w jakich sportach wygrywa ten, kto zgromadzi więcej punktów, a w jakich ten, który mniej. W każdym razie jeżeli ktoś wygra jednym punktem, to rozgrywka była dramatyczna. A czy są dyscypliny, w których zwycięzca meczu może mieć więcej punktów niż przegrany, ale może mieć mniej? Oczywiście - to takie konkurencje, w których aby zwyciężyć, trzeba wygrać więcej setów, a właśnie niekoniecznie pojedynczych punktów.

Wracajmy powoli do matematyki i fizyki. Pewnych kłopotów dostarcza nam „punkt w czasie”, chwila, moment, nieskończenie mały jego odcinek, nieskończenie razy mniejszy od mrugnięcia okiem. Filozoficzne problemy z tym związane dobrze ujął Henri Bergson (1859–1941, francuski filozof, laureat literackiej Nagrody Nobla w 1927 r.). Nie ma przeszłości - no, bo już jej nie ma. Nie ma przyszłości - bo jeszcze jej nie ma. Zostaje tylko teraźniejszość, tylko ona jest rzeczywista - ale jest realnością psychiczną. A czas, który znamy z równań fizycznych? To nie jest rzeczywisty czas, to fikcja czasu zarysowana na podobieństwo przestrzeni. Ale ten sztucznie skonstruowany czas jest nam niezbędny i dobrze sobie z tym radzimy. Każdy przecież intuicyjnie pojmuje, co to jest prędkość chwilowa. Jeżeli nawet przyspieszam albo zwalniam, jadąc samochodem, to w każdej chwili mam pewną prędkość. W każdej inną, ale zawsze jakąś. I nie przeszkadza nam to, że wzór

Podobne wątpliwości miał filozof George Berkeley, który oponował przeciwko rachunkowi różniczkowemu Newtona, argumentując właśnie, że jest to w końcu dzieleniem zera przez zero. Owszem, zero przez zero nie da się podzielić, ale rachunek różniczkowy działa znakomicie.

Rzucony do góry kamień zawisa na chwilę w powietrzu i dopiero potem spada z powrotem. „Na chwilę” - czyli na nieskończenie mały moment. Przyjrzyjmy się temu „punktowi w czasie”. Wyobraźmy sobie, że siatkarz wystawia piłkę koledze do ataku. Droga przebyta przez ciało w polu grawitacyjnym to

W czasie t= 0,1 sekundy od momentu „zawieszenia” piłka opadnie o 5 centymetrów. A zatem w czasie dwóch dziesiątych sekundy piłka znajduje się w pięciocentymetrowym odcinku (jedna dziesiąta do góry do szczytu i tyle samo w dół). Praktycznie jest to jeszcze mniejszy przedział, bo działa opór powietrza. Niewiele się zatem pomylimy, twierdząc, że wisi bez ruchu.

I tu przychodzi mi do głowy często spotykany, nawet u najwybitniejszych uczonych (że wymienię tylko Alberta Einsteina) motyw zadziwienia, że równania są mądrzejsze od nas, że jest w nich więcej, niż w nie włożyliśmy. W powieści Juliusza Verne’a „Podróż na Księżyc” wystrzeleni z armaty astronauci odczuwają - w miarę oddalania się od Ziemi - zmniejszanie siły przyciągania. Są coraz lżejsi, aż w pewnym punkcie podróży dopada ich nieważkość. Wtedy wyciągają szampana i zwyczajnie, po ziemsku, nalewają do kieliszków. Następnie zaczynają się przygotowywać na zwiększanie swojego ciężaru pod wpływem przyciągania Księżyca.

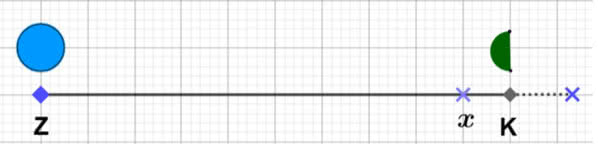
Dziś wiemy, jak to jest naprawdę, ale nie o to chodzi. Oto proste zadanie: gdzie jest taki punkt równowagi, że siły grawitacyjne Ziemi i Księżyc równoważą się? Pamiętamy, że siła ta działa proporcjonalnie do masy tych ciał niebieskich, a odwrotnie proporcjonalnie do kwadratu odległości miedzy nimi. Wiemy, że masa Księżyca to 1/81 masy Ziemi. Za jednostkę odległości weźmy dystans Ziemia-Księżyc. Niech punkt równowagi znajduje się na linii Ziemia-Księżyc w odległości od nas. Odległość do Księżyca to 1-x, rysunek 1.

Rysunek 1.

Układamy równanie:

Przekształcamy do równania kwadratowego, obliczamy „deltę” i po krótkiej chwili otrzymujemy dwa rozwiązania:

Pierwsze rozwiązanie jest zrozumiałe, punkt znajduje się w 9/10 drogi do Księżyca.

Ale równanie przypomniało też o drugim punkcie; znajdującym się za Księżycem. Gdybyśmy poszukali takich punktów nie tylko na prostej Ziemia-Księżyc, otrzymalibyśmy równanie niewielkiej elipsy wokół Księżyca.

Gdyby Ziemia i Księżyc nie były w ruchu, tylko tkwiły „jak słup” zawieszone w przestrzeni, ciało umieszczone w jednym z tych punktów też wisiałoby nieruchomo. Ale każdy z tych punktów jest niestabilny - najmniejsze wychylenie burzy tę kruchą równowagę - podobnie jest z postawieniem stożka na jego wierzchołku.

***

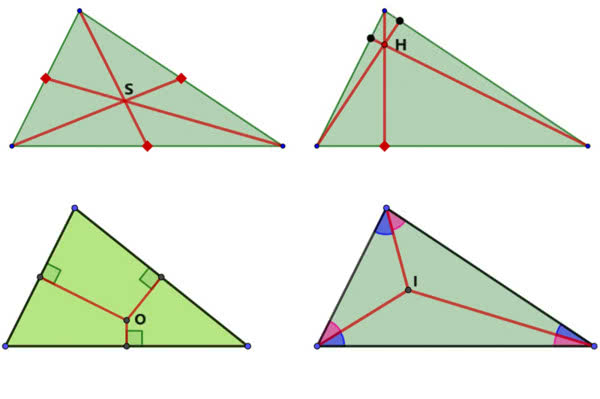
Znamy ze szkoły cztery podstawowe charakterystyczne punkty trójkąta. Są to: środek ciężkości (czyli punkt przecięcia środkowych, S), ortocentrum (czyli punkt wspólny wysokości, H), środek okręgu opisanego (czyli punkt wspólny trzech symetralnych, O) i środek okręgu wpisanego (I, w tym punkcie przecinają się dwusieczne kątów trójkąta). W tej kolejności są przedstawione na rysunku 2. Punkty te nie są całkiem dowolnie położone. Trzy pierwsze z nich leżą zawsze na jednej prostej, zwanej prostą Eulera. Co więcej, punkt S jest w jednej trzeciej odległości HO (rysunek 3). Punkt I leży „na uboczu”, ale też jest związany z pozostałymi ograniczeniami, o których tutaj nie wspomnę.

Rysunek 2.

Rysunek 3.

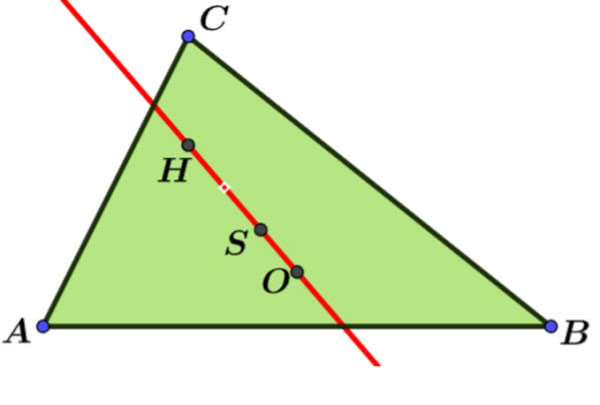
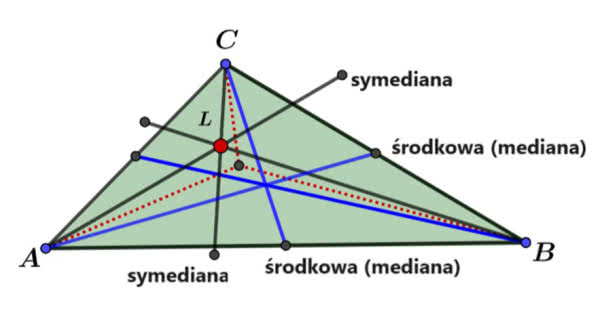
Rysunek 4 pokazuje inny ciekawy charakterystyczny punkt trójkąta, związany z tak zwanymi symedianami. Symediana to „lustrzana środkowa”: odbicie środkowej w dwusiecznej, wychodzącej z tego samego wierzchołka. Symediany przecinają się w jednym punkcie - zwanym punktem Lemoine’a trójkąta.

Rysunek 4.

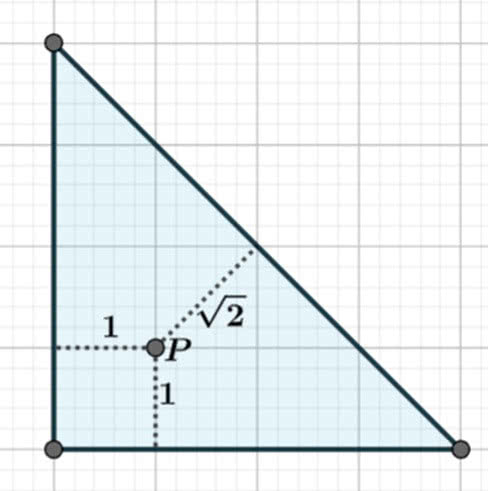
To całkiem ciekawy punkt - a w każdym razie ma „ciekawe współrzędne”. Są to specjalne współrzędne, zwane trójliniowymi. Otóż współrzędnymi trójliniowymi punktu P względem danego trójkąta nazywamy takie trzy liczby a,  b,  c,  że odległości punktu P od boków trójkąta są proporcjonalne do a, b, c. Środek trójkąta równobocznego ma oczywiście współrzędne 1, 1, 1, a punkt P na rysunku 5 - współrzędne (1, 1, √2). Wtedy środek okręgu opisanego na trójkącie ma współrzędne cosα, cosβ, cosγ, a punkt Lemoine’a współrzędne sinα, sinβ, sinγ.

Rysunek 5.

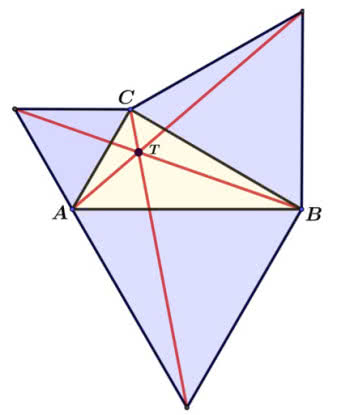
Do symetrii wrócę za chwilę. Z następnym punktem charakterystycznym trójkąta wiąże mnie kolejne „sentymentalne wspomnienie”. To był mój pierwszy kontakt z programem komputerowym, potrafiącym zgrabnie wykonywać obliczenia symboliczne - a nie tylko na konkretnych liczbach. Było to całkiem niedawno, bo prawie dokładnie 40 lat temu; w początkach lutego 1984 roku. „Skoro potrafisz wykonywać obliczenia na symbolach, to może nauczę cię geometrii analitycznej?” Maszyna zamrugała ochoczo i po pewnym czasie nauczyłem ją, jak się prowadzi prostą przez dwa punktu (to znaczy jak się wyznacza równanie tej prostej), jak się oblicza odległość, jak się pisze równanie okręgu i tak dalej. „No to teraz weź ogólny trójkąt, dobuduj trójkąty równoboczne na bokach, poprowadź odcinki jak na rysunku 6 i sprawdź, czy przecinają się w jednym punkcie”.

„Nie ma sprawy”, powiedziała maszyna. „Naciśnij, proszę, Enter. Proszę, oto masz zero na ekranie! Czy rozumiesz, że to znaczy, że trzy odcinki mają punkt wspólny? Naucz się mnie rozumieć!”

Być może w rzeczywistości było to trochę inaczej (i nałożyło mi się na obecne rozmowy z AI), ale tak czy owak, moim pierwszym dowodem komputerowym było właśnie to - dowód istnienia punktu Toricellego T trójkąta; bo tak się on właśnie nazywa (rysunek 6).

Rysunek 6.

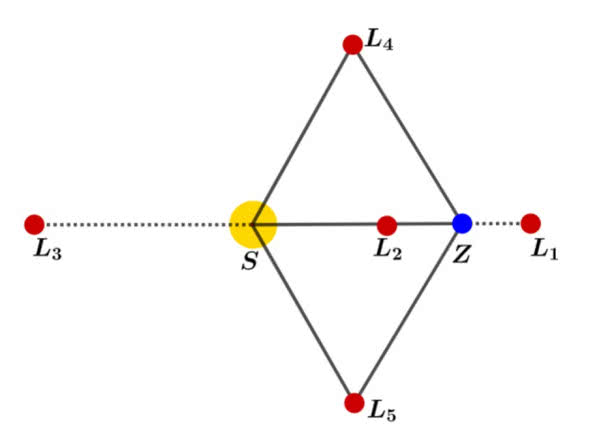
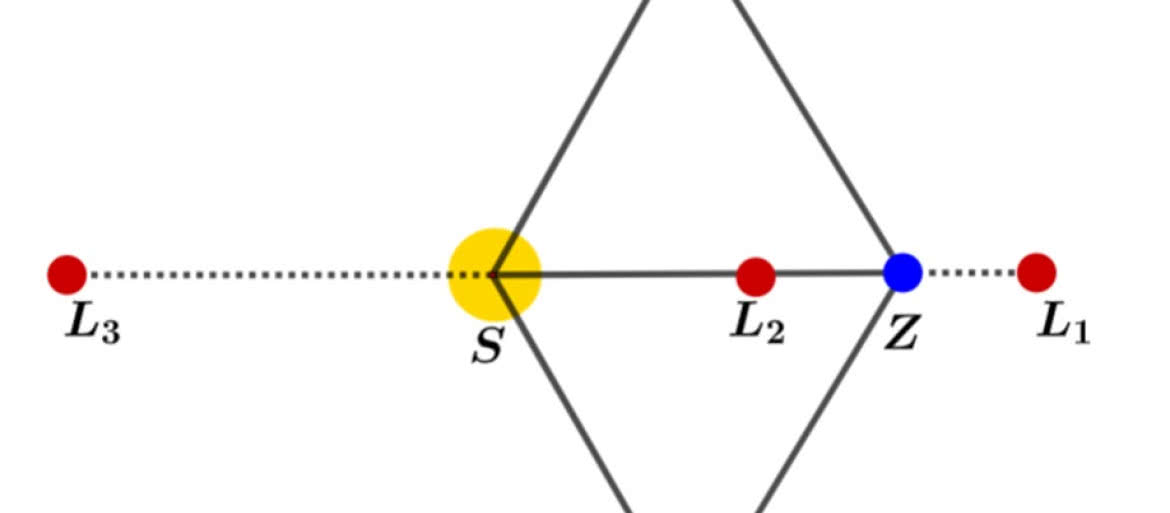
Właśnie to skojarzyło mi się z przejmującym odkryciem dwóch planetoid trojańskich naszej ojczyzny - Ziemi. W 1772 roku francuski astronom Joseph Lagrange wykazał matematycznie, że w układzie dwóch ciał istnieją tak zwane punkty libracyjne - w nich ciało o małej masie może stabilnie pozostawać w spoczynku - siły grawitacyjne i odśrodkowe równoważą się. Jest pięć takich punktów, oznaczanych jako L₁, L₂, L₃, L₄ i L₅. W układzie Słońce-Ziemia trzy pierwsze są na prostej łączącej nas z naszą gwiazdą macierzystą, a dwa pozostałe - w wierzchołkach trójkąta równobocznego. I to właśnie jest dla mnie niesamowite (rysunek 7). Gdzieś w głębokim kosmosie, gdzie Ziemia jest małą kropką, jest taki punkt, w którym można się zatrzymać, odpocząć, przystanąć. Jest to dla mnie psychologiczne trudne do przyjęcia - trochę tak, jak istniejąca podobno kiedyś w miesiącach zimowych karczma na Bałtyku. No, może porównanie jest nieco naciągane.

Rysunek 7.

Punkty libracyjne mają znaczenie w eksploracji kosmosu. Teleskop Webba jest umieszczony w L₂. Na ewentualne dotarcie do planetoidy tam się znajdującej potrzeba mniej paliwa niż do innych, równie odległych punktów kosmosu. Zaniepokoił mnie tylko komentarz autora jednego z opracowań, że może to ułatwić pozyskiwanie surowców naturalnych stamtąd.
Planetoidy na ogół tylko obiegają punkt libracyjny. Jest on bowiem stabilny - to znaczy przyciąga obiekty do siebie (jeżeli stosunek mas dwóch ciał jest dostatecznie duży). Pierwszą taką planetoidę odkrył niemiecki astronom Max Wolf w 1906 roku w układzie Słońce-Jowisz. Znajdowane następnie obiekty nazywano imionami bohaterów wojny trojańskiej.

Planetoidy należące do tak zwanego „obozu greckiego” wyprzedzają przy tym Jowisza w jego ruchu orbitalnym, poruszając się wokół punktu libracji L₄, a te należące do „obozu trojańskiego” podążają za planetą i skupiają się wokół punktu L₅. Znamy już wiele tysięcy Trojańczyków Jowisza, a także innych planet.

No, właśnie. Pierwszego Trojańczyka Ziemi odkryto w 2011 roku, a następnego w 2020 roku. Ten pierwszy jest dużą skałą, 300 metrów średnicy. Drugi jest większy, około 1800 metrów. Autorzy odkrycia starannie zbadali własności planetoidy i jej podługowatej orbity wokół L₅. Będzie nam towarzyszyć około 4000 lat, o ile słowo „towarzyszyć” jest na miejscu. Wykroczyłbym poza swoje kompetencje, gdybym próbował opisywać jej różne własności. Dla mnie, jako dla matematyka, jest fascynujące, że geometria szkolna się przydała i w głębokim kosmosie.

A na zakończenie rzecz ważna. Artykuł w „Nature” ma siedemnastu autorów. Jest wśród nich pani profesor Dagmara Oszkiewicz z Uniwersytetu im. Adama Mickiewicza w Poznaniu. 

Michał Szurek