Figury chiralne

Żeby łacińską literę L przekształcić na grecką "gammę" Γ, należy "wyjąć" ją z płaszczyzny i odbić w lustrze. Podobnie jest z R i rosyjskim Я (litera "ja"). To są figury chiralne: takie, które nie są identyczne ze swoim odbiciem lustrzanym. Zatem już wiesz, czytelniku, że Twoje dwie stopy są chiralne! Twoja prawa ręka w lustrze wygląda jak lewa, a jeżeli zaciąłeś się przy goleniu po lewej stronie (wersja dla Czytelniczek: pomalowałaś już prawą brew, a lewa jeszcze czeka) - lustro pokaże to odwrotnie. Czytałem kilka opowiadań science-fiction, w których kosmonauta po wielu, wielu latach podróży międzygwiezdnej wraca na Ziemię "odwrócony na lewą stronę" - czyli jako swoja chiralna kopia. Wydaje mu się, że to na Ziemi wszystko się zmieniło: piszemy dziwnymi literami a Anglicy zaczęli wreszcie jeździć normalnie, po prawej.
Uważamy, że życie musi być oparte na cząsteczkach chiralnych - inaczej nie bylibyśmy w stanie odróżnić lewej strony od prawej. Nie wiemy też, dlaczego życie wybiera zawsze tylko jedną z dwu możliwości. Aminokwasy, z których zbudowane są białka, są lewoskrętne, a cukry w naszym DNA - prawoskrętne. Czy nie moglibyśmy żyć harmonijnie z istotami odwrotnie skręconymi (tak, jak z osobami naturalnie leworęcznymi?) Można teoretycznie założyć, że byłoby możliwe "lewe" cukry i "prawe" aminokwasy, a jednak takich form życia nie ma. Pytanie "dlaczego" wykracza poza możliwości nauki? Tę chiralność życia wykorzystał ciekawie Stanisław Lem. W podróży numer 8 Ijon Tichy jest delegatem Ziemian na kongres Organizacji Planet Zjednoczonych. W krytycznym momencie przedstawiciel delegacji erydańskiej (tzn. pochodzący z Erydanii) nie zostawia na ludzkości suchej nitki, wykazując, że wzięliśmy się niejako z lewego łoża - nasz Stwórca mieszał aminokwasy w lewą stronę. Na szczęście okazuje się, że to był tylko sen bohatera (a raczej narratora) opowiadania.
Symetria, chiralność i regularność są zatem podstawami budowy świata. Może należy powiedzieć inaczej: jest podstawą naszego rozumienia świata. Tak zwany "chaos" jest też najczęściej wynikiem nałożenia regularnych procesów: tasowanie kart, zagniecenie ciasta, nieubłagane, ścisłe prawa rządzące nieprzewidywalnymi przypadkami. Matematyka powiada: jeżeli rzucisz 100000 razy monetą, to niekoniecznie otrzymasz 50000 razy orła, 50000 razy reszkę, ale masz 99% szans, że różnica między liczbą orłów i reszek będzie nie większa niż 1000, czyli jeden procent liczby rzutów. Wyjaśnia to znany ze szkoły schemat Bernoulliego. Ale nie o tym chciałem dziś napisać, a o prostych symetriach.
Choć uważam, że 90% wiadomości z Internetu to albo fake-news albo tendencyjnie napisane artykuły z naciągami faktami, to może wiadomość, którą się zainteresowałem, należy do tych pozostałych 10 procent. Chodzi o projekty wykorzystania pewnej rzadkiej sieci krystalicznej do budowy baterii słonecznych. Może to prawda.
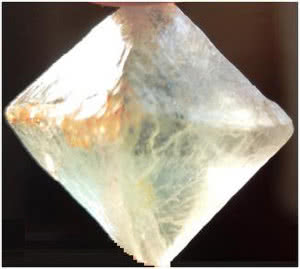
Od znajomego matematyka otrzymałem kilka lat temu w prezencie kryształ fluorytu - CaF2. Matematycznie jest to ośmiościan foremny. Taką bryłę tworzą środki ścian sześcianu. Ta matematyczna własność "pozwala" przyrodzie tworzyć kryształy o takim właśnie kształcie. Jest jeszcze 229 innych możliwości sieci krystalicznych. Dokładniej: matematyka wyjaśnia, że jest "tylko" 230 możliwych typów sieci krystalicznych (217, jeżeli chiralne będziemy uważać za te same). W dwóch wymiarach takich sieci jest tylko 17. Tyle może być zdobień ścian ornamentami, opartymi na powtarzalnym wzorze. Podkreślam, że nie oceniamy piękna takich zdobień i jak gdyby nie dostrzegamy zawsze interesującego łamania symetrii. Patrzymy tylko przez szkiełko i oko matematyka.
A skoro brniemy w matematykę, to powiem, że w przestrzeni czterowymiarowej takich możliwości jest 4894, w pięciowymiarowej - 222097, w sześciu - … ponad sto razy więcej. Ach, ile by było kryształów, gdyby dobry Pan Bóg stworzył nasz świat jako sześciowymiarowy… Ale byłoby z tym więcej kłopotów, niż nam się wydaje. To temat na inny artykuł - zostańmy w naszym trzecim wymiarze. Już starożytni Grecy propagowali umiar. Ale nawet w wymiarze 4, gdybym chciał wyliczyć wszystkie sieci, po 10 w jednym odcinku mojego kącika matematycznego, miałbym temat na … 40 lat. No, ale już po trzecim odcinku nikt by tego nie chciał czytać…
Zatem dla bezpieczeństwa ograniczę się do fryzów. Tak na to mówimy w matematyce. Podobny termin w technice frez ma nieco inne znaczenie - choć pewne podobieństwo jest. Wikipedia wyjaśnia, że fryz pochodzi od włoskiego fregio i jest to "pośredni, poziomy człon belkowania z reguły położony między architrawem i gzymsem; ogólnie - każdy poziomy pas dekoracyjny". Dla matematyka ważne jest to ostatnie określenie. Wymaga to jednak uściślenia. We fryzach występuje pewien podstawowy deseń, który jest przesuwany (teoretycznie bez końca w lewo i w prawo), tak, jakby choćby AAAAAAAA, EEEEEEEE, FFFFFFFF, OOOOOOOO, NNNNNNNN. Uprzedzając dalszą treść, zadam od razu zadanie: Co z innymi literami? Dalszy ciąg tekstu wyjaśni, o co w tym chodzi.
A właśnie, chodzi. Idziemy na spacer. Raz lewa noga w przedzie, raz prawa. W powieści Juliusza Verne’a W osiemdziesiąt dni dookoła świata, przerabianej kilkakrotnie na urocze filmy, pedantyczny Fileas Fogg chodzi do swojego klubu "Reforma", stawiając 1950 razy lewą nogę przed prawą i 1951 razy przeciwnie - a więc tak:
Z matematycznego punktu widzenia podobne naprzemienne ruchy wykonują biegacze narciarscy i para zawodników wiosłujących w kanadyjkach: jeden lewym wiosłem, a jego partner - prawym. Spójrzmy jeszcze raz na ten rysunek naszych stóp na mokrym piasku. Czy mamy tam - matematycznie rzecz biorąc - figurę symetryczną? Nie. Do osiągnięcia symetrii (osiowej, wzdłużnej) musielibyśmy skakać obunóż (zob. dalej, rys. 9). Taki deseń, jak na rys. 2, 3 i 4 ma tak zwaną symetrię z poślizgiem, czyli inaczej z przesunięciem. Narciarz wykonuje symetryczne, naprzemienne ruchy - ale między jednym a drugim już przesunął się o dwa-trzy metry.
Jak widać, nawiązuję do sportu. Co jest najpiękniejszą dyscypliną sportową? Nie mam wątpliwości - to ósemka wioślarska. Spójrzmy na moją układankę z klocków Lego (rys. 5). Który ornament ma tę samą treść matematyczną, co spacer ("raz jedna noga w przedzie, raz druga")? Może niełatwo zgadnąć, ale na pewno każdy przyzna mi rację - to szlaczek piąty od lewej. Czy każdy z Czytelników widzi, że ten piąty szlaczek, to "stop-klatki" takiej właśnie ósemki, wiosłującej do mety na skraju planszy? Widać nawet sternika, prawda?
Zobaczmy w tej układance inne dyscypliny. Pierwszy z lewej to kanadyjkarz (canoe). Wiosłuje jednym wiosłem z jednej strony, klęcząc niewygodnie na jednym kolanie. Porusza się "do przodu", odpowiednio balansując ciałem. Generuje najprostszy fryz - oparty tylko na przesunięciu, bez żadnych symetrii (rys. 6).
Jak opisać drugi szlaczek w układance na rys. 5? Przyszedł mi do głowy tylko prom, albo bardzo dawny parostatek, mający koło napędowe z jednej strony. Trzeci wzór może opisywać ruchy pływaka w stylu motylkowym (fachowo: delfin), albo dwójki podwójnej w wioślarstwie. Czwarty to zwykła dwójka, wioślarska albo kanadyjkowa. Mamy w niej dwóch chiralnych zawodników - w mojej układance ten na nosku ciągnie prawym wiosłem, ten na szlaku - lewym. Na szóstym widzę samolot. Mieszkam pod korytarzem powietrznym wiodącym z lotniska Okęcie. Widzę, że wznoszące się samoloty migają naprzemiennie światłem na lewym skrzydle i na prawym. Siódmy ornament różni się od czwartego tym, że żółte klocki są w środku. Czy widzimy tam ptaka, zrywającego się do lotu?
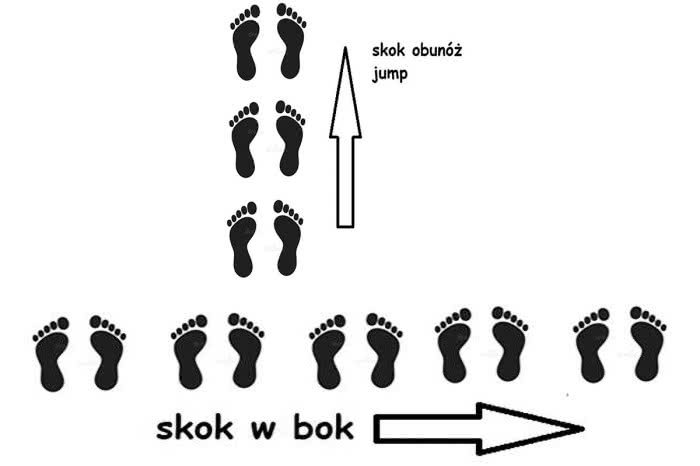
Poskaczmy jeszcze na dwóch nogach. Można do przodu, albo w bok:
Ten fryz ma jedną symetrię podłużną - to znaczy względem osi wyznaczającej kierunek ruchu. Ten na rysunku 10 jest symetryczny względem osi prostopadłej do kierunku ruchu.
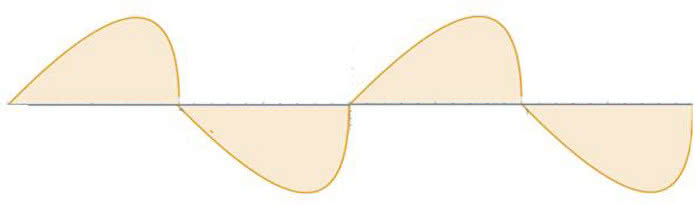
Są jeszcze symetrie obrotowe. Obróćmy tekst "do góry nogami" - szlaczek zostanie taki sam: na górze naprzemiennie czerwone i niebieskie garbki, na dole zwisające girlandy, też na przemian czerwone i niebieskie.
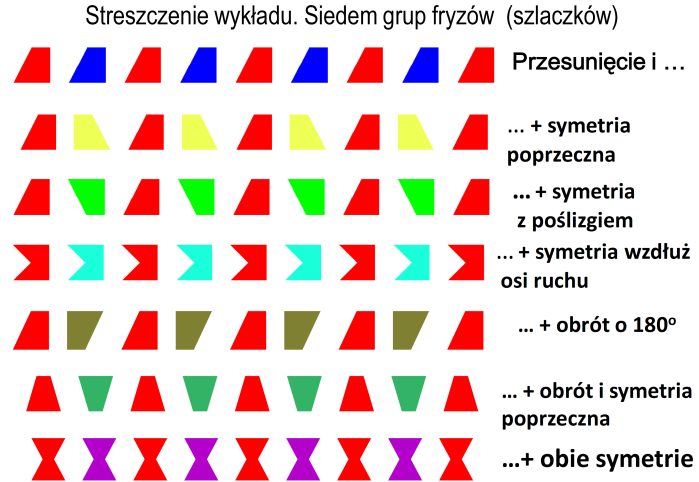
Podsumujmy. Nie jest trudno wykazać, że innych fryzów nie ma. Podkreślam - z matematycznego punktu widzenia. Zestawienie widzimy na rysunku 13.
Ważna uwaga. Artykuł był streszczeniem wykładu, jaki miałem dla studentów PAN-owskiej Wyższej Szkoły Informatyki Stosowanej i Zarządzania. Koronawirus wymusił atrakcyjną formę, którą mogłem tu przekazać. Proste dowody matematyczne opuściłem. Nie będę też uczyć studentów "prawdziwej" krystalografii - to nie mieści się w profilu Szkoły. Ale wycieczka w tę stronę każdemu dobrze zrobi.
Michał Szurek