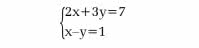Koronawirus i nauczanie matematyki - zbiory częściowo uporządkowane

Wiosną 2020 roku nie ja jeden odkryłem, że lekcje (w tym wykłady, ćwiczenia itp.) można bardzo efektywnie prowadzić zdalnie (Google Meet, Microsoft Teams, etc.), za cenę dużej pracy ze strony nauczającego i po prostu chęci "bycia kształconym" po drugiej stronie; ale i z pewną wygodą: siedzę we własnym domu, na własnym fotelu, a na tradycyjnych wykładach studenci też często-gęsto zajmowali się czym innym. Efekty takiego nauczania mogą być nawet lepsze niż przy tradycyjnym, pochodzącym jeszcze ze średniowiecza, systemie klasowo-lekcyjnym. Co nam z tego zostanie, gdy wirus sobie pójdzie "w cholerę"? Sądzę, że … dość dużo. Ale zobaczymy.
Opowiem dzisiaj o zbiorach częściowo uporządkowanych. To proste. Bo dwuargumentowa relacja w niepustym zbiorze X nazywa się relacją częściowego porządku, gdy jest
Kto nie jest samoukiem, jest nieukiem!
(Tadeusz Kotarbiński, 1886–1981, filozof,
prezes Polskiej Akademii Nauk w latach 1957–1962).
- Zwrotna, tzn. dla każdego x ∈ X jest x « x,
- Przechodnia, tzn. jeżeli x « y, oraz y « z, to x « z,
- Na wpół przeciwsymetryczna, tzn. (x « y ∧ y « x)→x = y.
Łańcuchem nazywamy zbiór o następującej własności: dla każdych dwóch elementów x, y tego zbioru jest albo x « y albo y « x y x. Antyłańcuch to ….
Stop, stop! Czy coś z tego da wyrozumieć? Oczywiście, że w końcu tak. Ale czy ktoś z Czytelników (nieznających tego skądinąd) już pojął, o co tu biega?
Nie sądzę! A taki jest kanon nauczania matematyki. Również w szkole. Najpierw porządna, ścisła definicja, a potem, ci, którzy nie zasnęli z nudów, na pewno coś pojmą. Taką metodę narzucili "wielcy" dydaktycy matematyki. Ma być porządnie i ściśle. To prawda, że w końcu tak ma być. Matematyka ma być nauką ścisłą (zobacz także: Równania, kody, szyfry, matematyka i poezja).
Muszę się przyznać, że w szkole wyższej, w której pracuję po przejściu na emeryturę z Uniwersytetu Warszawskiego, też tak uczyłem przez wiele lat. Dopiero wymuszona przez koronawirusa konieczność zdalnego nauczania była przysłowiowym kubłem zimnej wody (niech tak zostanie: konieczność była kubłem!). I nagle z wysokiej abstrakcji zrobiło się lekko i przyjemnie. Dla ustalenia uwagi: lekko to nie znaczy łatwo. Bokser wagi lekkiej też nie ma łatwo.
Uśmiechnę się do własnych wspomnień. Podstawy matematyki wykładała mi ówczesna pani dziekan wydziału, matematyczka z najwyższej półki, świeżo po dłuższym pobycie w USA, co w owych czasach samo w sobie było czymś nadzwyczajnym. Sądzę, że trochę snobowała się, że trochę zapomniała języka polskiego. Nadużywała staropolskich "ów", "przeto", "azaliż" i wymyśliła to określenie: "relacja na wpół przeciwsymetryczna". Używam go z lubością, jest w gruncie rzeczy trafny. Podoba mi się. Ale nie wymagam tego od studentów. Zwykle mówi się na to "słaba antysymetria". Tyz piyknie.
Dawno, dawno temu, bo w latach siedemdziesiątych (zeszłego wieku) zrobiono wielką, radosną reformę nauczania matematyki. Zbiegło się to z początkiem krótkiego okresu rządów Edwarda Gierka - pewnym otwarciem się naszego kraju na świat. "Dzieci też można uczyć matematyki wyższej" krzyczeli Wielcy Dydaktycy. Zrobiono dzieciom streszczenie uniwersyteckiego wykładu Podstaw Matematyki. Taki był trend nie tylko u nas, ale w całej Europie. Nie wystarczyło rozwiązać równanie, ale trzeba było objaśnić każdy szczegół. Żeby nie być gołosłownym - każdy z Czytelników umie rozwiązać układ równań:
ale uczniowie musieli uzasadniać każdy krok, powoływać się na stosowne twierdzenia itd. Był to klasyczny przerost formy nad treścią. Łatwo mi teraz krytykować. Też byłem kiedyś zwolennikiem takiego podejścia. Jest podniecające … dla młodzieńców zafascynowanych matematyką. A taki oczywiście byłem (i, dla ustalenia uwagi, jestem).
Ale wystarczy już dygresji, przejdźmy do konkretu: wykład, który był "teoretycznie" przeznaczony dla studentów drugiego roku studiów politechnicznych i byłby tak suchy, jak wiórki kokosowe, gdyby nie COVID-19. Trochę przesadzam…
Dzień dobry państwu. Tematem na dzisiaj są częściowe porządki. Nie, nie jest to aluzja do niestarannego sprzątania. Lepszym porównaniem byłoby rozważanie, co jest lepsze: zupa pomidorowa, czy ciastko z kremem. Odpowiedź jest zrozumiała: zależy do czego. Na deser - ciastko, a jako pożywne danie: zupa.
W matematyce zajmujemy się liczbami. Są one dobrze uporządkowane: są większe i mniejsze, ale z dwóch różnych liczb zawsze jedna jest mniejsza, a zatem ta druga - większa. Są po kolei, tak, jak litery w alfabecie. W dzienniku lekcyjnym kolejność może być taka: Adamczyk, Bagińska, Chojnicki, Derkowski, Elget, Filipow, Grzechnik, Holnicki (to koleżanki i koledzy z mojej klasy!). Nie mamy też wątpliwości, że Matusiak « Matuszelański « Matuszewski « Matysiak. Symbol "podwójnej nierówności" ma tu znaczenie "poprzedza".
W moim kółku turystycznym, staramy się układać listy alfabetycznie, ale według imion, a zatem Alina Wrońska « Barbara Kaczarowska « Cezary Bowszyc itd. W oficjalnych sprawozdaniach kolejność byłaby odwrotna. Porządek alfabetyczny matematycy nazywają leksykograficznym (leksykon to mniej więcej to samo, co słownik). Natomiast porządek taki, w którym w dwuczłonowej nazwie (Michał Szurek, Alina Wrońska, Stanisław Smarzyński) patrzymy najpierw na drugi człon, jest dla matematyków porządkiem antyleksykograficznym. Długie nazwy, ale treść przecież bardzo prosta.
Wszystkie takie porządki są nazywane porządkami liniowymi. Porządkujemy po kolei: pierwszy, drugi, trzeci. Wszystko jak po sznurku, od pierwszej pozycji do ostatniej. Nie zawsze to ma sens. Książek w bibliotece nie ustawiamy przecież w ten sposób, tylko działami. Dopiero w obrębie działu porządkujemy liniowo (zwykle alfabetycznie).
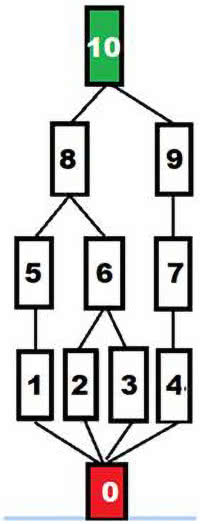
Przy większych projektach, szczególnie w pracy zespołowej, nie mamy już porządku liniowego. Spójrzmy na rys. 3. Chcemy zbudować mały hotelik. Mamy już pieniądze (komórka 0). Załatwiamy zezwolenia, gromadzimy materiały, zaczynamy budowę, ale równolegle prowadzimy kampanię reklamową, szukamy pracowników i tak dalej, i tak dalej. Gdy osiągniemy "10", do hotelu mogą wprowadzić się pierwsi goście (przykład pochodzi z opowieści p. Dąbrowskich i ich hoteliku na przedmieściach Krakowa). Mamy porządek nieliniowy - niektóre sprawy toczyć się mogą równolegle.
Na zajęciach z ekonomii poznają państwo pojęcie ścieżki krytycznej. Jest to zestaw czynności, które trzeba wykonać po kolei (i to w matematyce nazywa się łańcuchem, o tym za chwilę), a które trwają najdłużej. Skrócenie czasu budowy to przeorganizowanie ścieżki krytycznej. Ale o tym na innych wykładach (przypominam, że prowadzę "wykład uniwersytecki"). Skupiamy się na matematyce.
Takie diagramy, jak na rysunku 3, nazywają się diagramami Hassego (Helmut Hasse, matematyk niemiecki, 1898 - 1979). Każde złożone przedsięwzięcie winno być tak zaprojektowane. Widzimy ciągi czynności: 1-5-8-10, 2-6-8, 3-6, 4-7-9-10. Matematycy nazywają je właśnie łańcuchami. Całość przedsięwzięcia to cztery łańcuchy. Natomiast grupy czynności 1-2-3-4, 5-6-7 i 8-9 to antyłańcuchy. Tak się nazywają. Chodzi o to, że w poszczególnej grupie żadna z czynności nie zależy od poprzedniej.
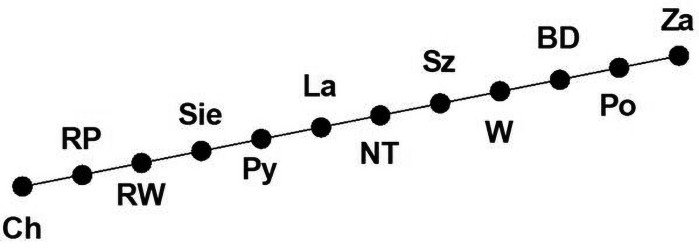
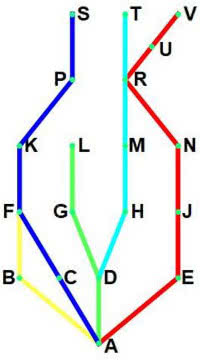
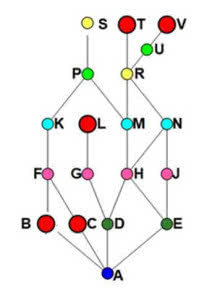
Przejdźmy do rysunku 4. Co się narzuca? Ależ to może być schemat metra w jakimś mieście! Kolejki podziemne są zawsze pogrupowane w linie - nie przejeżdżają z jednej na drugą. Łańcuchy to poszczególne linie. W mieście z rys. 4 jest pięć linii (zapamiętajmy, że pięć jest napisane "boldem" - po polsku nazywa się to półgruby).
Na schemacie tym (rys. 4) jest króciutka żółta ABF, sześciostacyjna ACFKPS, zielona ADGL, błękitna DHMRT i najdłuższa czerwona. Matematyk powie: w tym diagramie Hassego jest pięć łańcuchów. Na czerwonej linii jest siedem stacji: AEJNRUV. Co z antyłańcuchami? Jest ich siedem. Czytelnik już zauważył, że podkreśliłem dwa razy słowo siedem.
Antyłańcuch to taki zestaw stacji, że z żadnej z nich nie da się dojechać do drugiej bez przesiadki. Gdy trochę "pokombinujemy", zobaczymy takie antyłańcuchy: A, BCLTV, DE, FGHJ, KMN, PU, SR. Proszę sprawdzić, np. z żadnej ze stacji BCLTV nie da się przejechać do innej BCTLV bez przesiadki, a dokładniej: bez konieczności powrotu stacji narysowanej niżej. Ile jest antyłańcuchów? Siedem. Jaki rozmiar ma największy z nich? Pięć (znów napisana krojem półgrubym).
Domyślacie się, studenci, że zbieżność tych liczb nie jest przypadkowa. Tak jest. Odkrył to i udowodnił (tzn., że zawsze tak jest) w 1950 roku Robert Palmer Dilworth, (1914-1993, matematyk amerykański). Liczba łańcuchów potrzebnych do pokrycia całego zbioru jest równa rozmiarowi największego antyłańcucha i odwrotnie: liczba antyłańcuchów jest tą samą liczbą, co długość najdłuższego łańcucha. Tak jest zawsze w zbiorze częściowo uporządkowanym, czyli takim, który można zobrazować diagramem Hassego. Nie jest to całkiem ścisła i poprawna definicja. Coś takiego matematycy nazywają "working definition". Jest to trochę co innego, niż "pracująca definicja". Jest to wskazówka, jak należy patrzeć, jak należy rozumieć zbiory częściowo uporządkowane. To jest ważny element każdego uczenia się: zobaczyć, jak to działa.
Angielskim skrótem od partially ordered set jest poset - to słowo ładnie brzmi w językach słowiańskich, trochę tak, jak oset. Zwróćmy uwagę, że oset jest też rozgałęziony jak poset.
Bardzo ładnie, ale po co to komu? Wam, drodzy studenci, jest to potrzebne do zdania egzaminu i to jest chyba wystarczający powód, żeby się tego uczyć. Słucham, jakie są pytania? Słucham, pan spod okna. Aha, pytanie brzmi, czy kiedykolwiek przyda się to Panu w życiu? Może i nie, ale komuś bystrzejszemu od Pana to z pewnością… Może do analizy ścieżki krytycznej przy skomplikowanym projekcie ekonomicznym?
Piszę ten tekst w połowie czerwca, na Uniwersytecie Warszawskim trwają wybory rektora. Przeczytałem kilka komentarzy internautów. Zaskakująco dużo jest nagonki (czyli "hejtu") na "wykształciuchów". Ktoś napisał dosadnie, że ludzie z wykształceniem uniwersyteckich umieją mniej niż ci po zawodówkach. Nie wdam się oczywiście w dyskusję. Jest mi tylko smutno, że wraca mocno ugruntowany w PRL pogląd, że i tak wszystko się da zrobić za pomocą młotka i przecinaka. Wracam do matematyki.
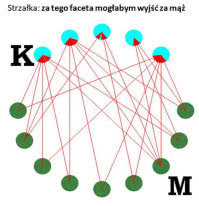
Twierdzenie Dillwortha ma kilka ciekawych zastosowań. Jedno z nich znane jest pod nazwą twierdzenia o małżeństwach (rys. 6).
Jest grupa kobiet (dziewcząt raczej) i trochę większa grupa mężczyzn. Każda dziewczyna myśli mniej więcej tak: "za tego mogłabym się wydać, za tego drugiego też, ale za tego trzeciego to nigdy w życiu". I tak, dalej, każda ma preferencje. Rysujemy diagram, prowadząc do każdej z nich strzałkę od tego z facetów, którego nie odrzuca jako kandydata do ołtarza. Pytanie: czy można tak skojarzyć pary, żeby każda znalazła męża, którego akceptuje?
Twierdzenie, którego autorem jest Philip Hall, mówi, że da się tak zrobić - jeżeli spełnione są pewne warunki, których tu nie będę omawiać (to na następnym wykładzie, proszę studentów). Zauważmy jednak, że o zadowoleniu mężczyzn się tutaj w ogóle nie mówi. Jak wiadomo, to kobiety wybierają nas, a nie odwrotnie, jak się nam wydaje (przypominam, że jestem autorem, nie autorką).
Trochę poważnej matematyki. Jak twierdzenie Halla wynika z Dilwortha? Bardzo prosto. Spójrzmy jeszcze raz na rys. 6. Łańcuchy są tam bardzo krótkie: mają długość 2 (biegną w kierunku M-K). Zbiór mężczyzn stanowi antyłańcuch (właśnie dlatego, że strzałki są tylko w kierunku M-K). Można zatem pokryć cały zbiór tyloma antyłańcuchami, ilu jest mężczyzn. A zatem do każdej kobiety dobiegnie strzałka. A to znaczy, że może się wydać za faceta, którego akceptuje!!!
Zaraz, zaraz, zapyta ktoś, i to wszystko? To ma być całe zastosowanie? Hormony jakoś się dogadają i po co matematyka? Po pierwsze to nie całe zastosowanie, a tylko jedno z dużej serii. Spójrzmy na jedno z nich. Niech K (rys. 6) nie oznacza przedstawicielek lepszej płci, tylko prozaicznie Klientów, a M - to marki np. samochodów, pralek, środków na schudnięcie, oferty biura podróży, itp. Każdy klient ma marki, które akceptuje i które odrzuca. Czy i jak da się zrobić, by każdemu coś sprzedać? Tu nie tylko kończą się żarty, ale i wiedza autora artykułu na ten temat. Wiem tylko, że analiza oparta jest na matematyce z całkiem wysokiej półki.
Nauczanie matematyki polega w szkole na trenowaniu algorytmów. To ważna część tresury. Ale powoli odchodzimy w stronę nauczania nie tyle matematyki, co metody matematycznej. Dzisiejszy wykład był właśnie o tym: mówimy o abstrakcyjnych konstrukcjach myślowych, myślimy o codzienności. Mówimy o łańcuchach i antyłańcuchach w zbiorach z relacją zwrotną, przechodnią i jeszcze inną, stosujemy w modelach sprzedawca-klient. Każde obliczenie wykona za nas komputer. Modeli matematycznych jeszcze nie stworzy. W myśleniu wciąż z nim wygrywamy. Zresztą, oby jak najdłużej!
Michał Szurek