Trójkąt równoboczny

Na zjazdy SNM jeżdżę od wielu lat i zawsze staram się opowiadać o matematyce w konwencji „matematyka wokół nas”. Opowiadałem o najbardziej symetrycznym wśród trójkątów: trójkącie równobocznym. To ładna figura. Symbolizuje równowagę. Nie wywołuje napięć, związanych z przeciwieństwami - tak jak to czyni prostokąt.
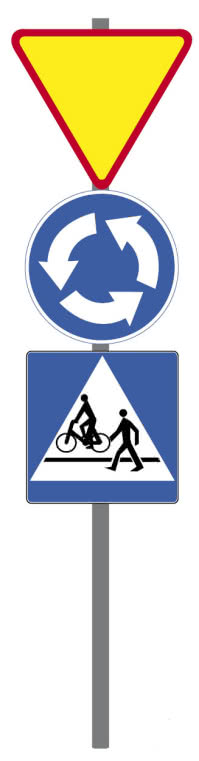
Prawie każdy z nas widzi codziennie jeden trójkąt równoboczny. To ważny dla kierowców znak A-7: To znak A-7, „ustąp pierwszeństwa przejazdu”. Przypomina odwrócony znak nierówności <, w którym mniejsze staje się większe. Jedziemy drogą podrzędną i wjeżdżamy na główną. Nie musimy się zatrzymywać jak przed ośmiokątnym znakiem B-20, ale musimy się uważnie rozejrzeć w lewo i w prawo. Muszą to czynić nawet kierowcy samochodów marki Mercedes (1), a skoro mowa o geometrii w kontekście ruchu drogowego, to zwróćmy uwagę na ciekawe połączenie trójkąta, koła i kwadratu koła przy wjeździe na rondo (2.)
Znamy też Trójkąt Bermudzki, o wierzchołkach w Miami na Florydzie, w Porto Rico i właśnie na Bermudach. Działają tam podobno jakieś tajemnicze siły. Okręty i samoloty przepadają bez śladu, a jedna z teorii mówi, że to z powodu występujących w tym trójkącie anomalii czasu. Można się przenieść do zamierzchłej przeszłości i zniknąć dla współczesnych. Bywa, że chciałbym skorzystać z tej możliwości.
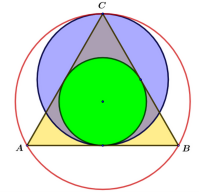
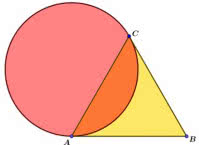
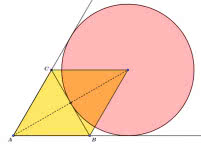
Jak wspomniałem na wstępie, mówiłem do nauczycieli, a zatem dużo było o geometrii szkolnej. Geometria to przede wszystkim wielokąty, odcinki i okręgi. Mam pewien sentymentalny stosunek do okręgów i kul - może dlatego, że moja najważniejsza praca naukowa dotyczyła geometrii kuli czterowymiarowej. A zatem popatrzmy na okręgi związane z trójkątem. Na rysunku 3 widzimy okręgi związane zresztą z każdym trójkątem: wpisany, opisany oraz przechodzący przez wierzchołek i styczny do przeciwległego boku. Jest także czwarty, równie charakterystyczny okrąg (4). Jest styczny do dwóch boków trójkąta w jego wierzchołkach. Jak każdy trójkąt, tak i równoboczny ma trzy okręgi dopisane, oczywiście takie same. Na rysunku 5 widzimy jeden z nich.
Nie ma matematyki bez zadań.
Zadanie 1. Wyznacz promienie okręgów, widocznych na rysunkach 3 i 4, gdy boki trójkąta ABC mają daną długość a. Oblicz promień okręgu dopisanego.
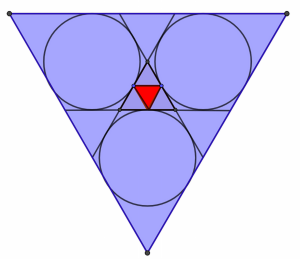
Zadanie 2. Oblicz stosunek pól trójkątów na rysunku 6 – tego najmniejszego w środku i największego (niebieskiego).
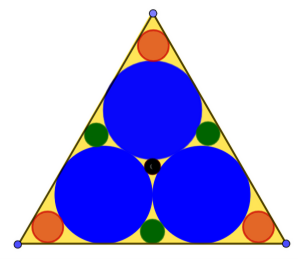
Zadanie 3. Oblicz promienie kół widocznych na rysunku 7. Jak zwykle, zakładamy, że wyjściowy trójkąt ma bok długości a.
Jednym z najładniejszych twierdzeń, w których występują trójkąty równoboczne, jest nazywane powszechnie twierdzeniem Napoleona, chociaż nikt nie wie dlaczego. Być może cesarz istotnie je odkrył, pokazał komuś, ale nic nie zostało nigdzie zapisane, bo przecież wszyscy z otoczenia cesarza mieli inne sprawy na głowie. Ale niech nazwa zostanie.
Twierdzenie Napoleona. Jeżeli na bokach dowolnego trójkąta dobudujemy trójkąty równoboczne, to ich środki też będą tworzyły trójkąt równoboczny.
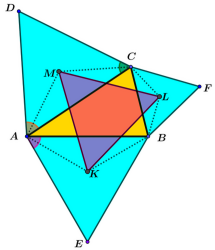
Dowód jest ładniejszy niż samo twierdzenie. Z rachunku na kątach otrzymujemy od razu, że kąty MAK i CAE na rysunku są równe (mają równe miary), a zatem trójkąty ACE i MAK są podobne. Skalą podobieństwa jest, bo taki jest stosunek długości boku trójkąta równobocznego do odległości środka trójkąta równobocznego do długości boku. Podobne rozumowanie pokazuje, że w tej samej skali podobne są trójkąty BCE i BLK. Stąd wynika, że |LM| = |MK|. Podobnie wykazujemy, że kolejne pary boków mają równe długości i wobec tego trójkąt KLM jest równoboczny.
Zadanie 4. Wyznacz długość boku „trójkąta Napoleona”, to znaczy boku trójkąta równobocznego KLM, gdy trójkątem wyjściowym ABC jest trójkąt równoramienny prostokątny o podstawie a.
Zadanie 5. Wyznacz długość boku „trójkąta Napoleona”, to znaczy boku trójkąta równobocznego KLM, gdy trójkątem wyjściowym ABC jest „połowa trójkąta równobocznego”, to znaczy trójkąt o kątach 30o, 60o, 90o.
***
Trójkąt równoboczny pojawia się w zdumiewającym twierdzeniu, sformułowanym w 1899 roku przez angielsko-amerykańskiego matematyka Franka Morleya (1860–1937). Zakomunikował je znajomym, ale dowodu nie podał, a widocznie nikomu nie chciało się go szukać. Twierdzenie Morleya nazwano potem „ostatnim twierdzeniem geometrii euklidesowej”, ale jest to podobne do oświadczenia prezesa amerykańskiego biura patentowego, który podobno (tak twierdził Julian Tuwim) w 1882 roku powiedział, że „niewielu wynalazków należy się spodziewać w przyszłości, bo praktycznie wszystko zostało już wynalezione”.
Twierdzenie Morleya. Proste dzielące kąty trójkąta na trzy równe części ograniczają trójkąt równoboczny (9).
***
Z bogatego zestawu różnych innych konfiguracji, gdzie pojawiają się trójkąty równoboczne, wybrałem jeszcze trzy. Udowodnienie tych własności, sugerowanych przez rysunki, może być trudne - pochodzą z zadań z olimpiad matematycznych.
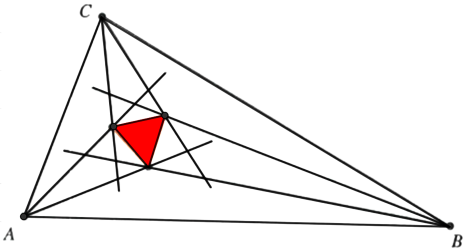
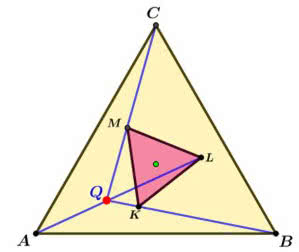
Na rysunku 10 wewnątrz trójkąta równobocznego ABC wybrano inny trójkąt równoboczny KLM, jednakże o tym samym środku, co ABC. Wtedy proste łączące odpowiednie wierzchołki przecinają się w jednym punkcie.
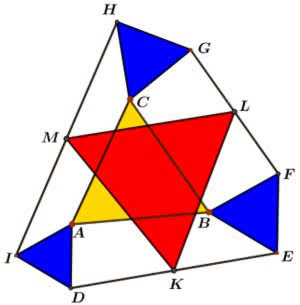
Własność, pokazana na rysunku 11, jest jeszcze bardziej złożona. Do wierzchołków trójkąta równobocznego ABC doczepiono trójkąty równoboczne dowolnych rozmiarów. Punkty K, L, M są środkami odcinków DE, FG i HI i tworzą, jak widać, trójkąt równoboczny. Oczywiście „widać” nie jest żadnym dowodem.
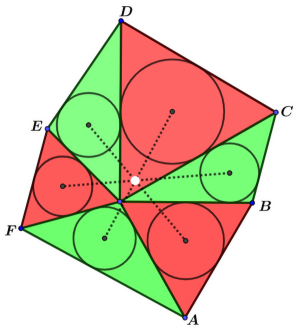
Najbardziej skomplikowana i intrygująca jest własność, którą sugeruje następny rysunek 12. Mamy trzy trójkąty równoboczne, stykające się „dzióbkami” - to te trójkąty o podstawach AB, CD i EF. Uzupełniamy całość do sześciokąta. Tworzą się nowe trójkąty, te o podstawach BC, DE i FA. W każdy trójkąt wpisujemy okrąg. Wtedy proste łączące środki okręgów, wpisanych w przeciwległe trójkąty, mają punkt wspólny.
***
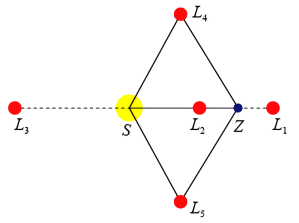
Na zakończenie odlecimy w kosmos. Odkryto niedawno (lata 2011–2020), dwie planetoidy trojańskie naszej planety Ziemi. Otóż w 1772 roku francuski astronom Joseph Lagrange wykazał matematycznie, że w układzie dwóch ciał istnieją tak zwane punkty libracyjne - w nich ciało o małej masie może stabilnie pozostawać w spoczynku - siły grawitacyjne i odśrodkowe równoważą się. Oczywiście w kosmosie nie można po prostu przystanąć i tkwić jak słup. Satelita geostacjonarny też wisi w jednym punkcie, ale pędzi wraz z Ziemią po orbicie. Podobnie jest z punktami libracyjnymi. Jest pięć takich punktów, oznaczanych przez L1, L2, L3, L4 i L5. W układzie Słońce–Ziemia trzy pierwsze są na prostej łączącej
nas z naszą gwiazdą macierzystą, a dwa pozostałe – w wierzchołkach trójkąta równobocznego. I to właśnie jest dla mnie niesamowite. Gdzieś w głębokim kosmosie, gdzie Ziemia jest małą kropką, jest taki punkt, w którym można się zatrzymać, odpocząć, przystanąć. Jest to dla mnie psychologicznie trudne do przyjęcia – trochę tak, jak istniejąca podobno kiedyś
w miesiącach zimowych karczma na Bałtyku. No, może porównanie jest nieco naciągane.
Teleskop Webba jest umieszczony w L2. Na ewentualne dotarcie do planetoidy tam się znajdującej potrzeba mniej paliwa niż do innych, równie odległych punktów kosmosu. Zaniepokoił mnie tylko komentarz autora jednego z opracowań, że może to ułatwić pozyskiwanie surowców naturalnych stamtąd.
Planetoidy na ogół tylko obiegają punkt libracyjny. Jest on bowiem stabilny – to znaczy przyciąga obiekty do siebie (jeżeli stosunek mas dwóch ciał jest dostatecznie duży). Pierwszą taką planetoidę odkrył niemiecki astronom Max Wolf w 1906 roku w układzie Słońce–Jowisz. Znajdowane następnie obiekty nazywano imionami bohaterów wojny trojańskiej. Planetoidy należące do tak zwanego „obozu greckiego” wyprzedzają przy tym Jowisza w jego ruchu orbitalnym, poruszając się wokół punktu libracyjnego L4, a te należące do „obozu trojańskiego” podążają za planetą i skupiają się wokół punktu L5.
Pierwszego Trojańczyka Ziemi odkryto w 2011 roku, a następnego w 2020 roku. Ten pierwszy jest dużą skałą, 300 metrów średnicy. Drugi jest większy, około 1800 metrów. Będzie nam towarzyszyć około 4000 lat, o ile słowo „towarzyszyć” jest na miejscu. Dla mnie, jako matematyka, jest fascynujące, że geometria szkolna się przydała i w głębokim kosmosie. I jeszcze rzecz ważna. Artykuł w „Nature”, przedstawiający tego drugiego Trojańczyka, ma siedemnastu autorów. Jest wśród nich Dagmara Oszkiewicz z Uniwersytetu im. Adama Mickiewicza w Poznaniu.
Odpowiedzi do zadań
Michał Szurek