Problem ośmiu hetmanów

Komplet 92 rozwiązań problemu opublikował dwa lata później nauczyciel matematyki ze Schleusingen (w Turyngiii, Niemcy) Franz Nauck w wydawanej w Lipsku "Illustirte Zeitung". Problemem tym zajmował się też wybitny niemiecki matematyk Carl Friedrich Gauss (1777-1855) (3). Początkowo rozważano zwykłą szachownicę (n=8), ale potem rozszerzono problem hetmanów z ośmiu do n, czyli szukanie sposobów rozmieszczenia n hetmanów na planszach n×n.
Nauck doszedł do wszystkich możliwych ustawień, korzystając ze schematycznej, żmudnej metody prób i błędów. Współcześnie odpowiada jej "siłowy" algorytm z nawrotami, zwany backtrackingiem, który przy zastosowaniu szybkiego komputera daje błyskawicznie komplet rozwiązań. Gauss zauważył możliwość przekształcenia zadania szachowego, a właściwie geometrycznego w arytmetyczne.
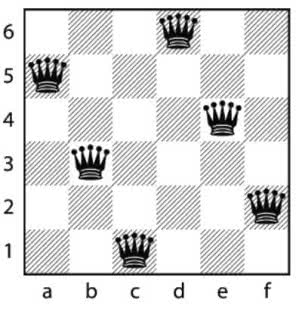
Charakterystyczną cechą rozwiązań jest ustawienie hetmanów w "relacji skoczka". W przypadku klasycznej szachownicy 8×8 istnieją 92 rozwiązania, z których podstawowych jest 12, a resztą to warianty odwrócone (pokrewne pozycje wynikające z odbić zwierciadlanych i obrotów) (4, 5).
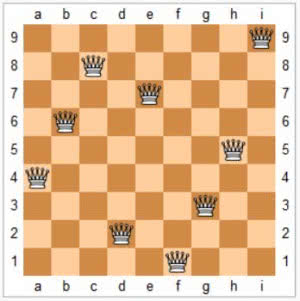
Przykładowe rozwiązania ustawienia hetmanów na planszach 4×4, 5×5, 6×6, 9×9 i 10×10 przedstawione są na diagramach 6-10.
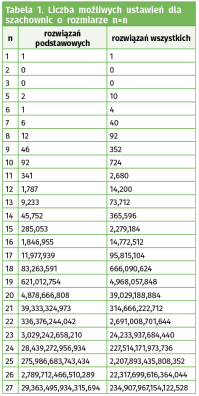
Przed pięciu laty, po ponad roku pracy komputerów na Technische Universität Dresden ustalono, że 27 hetmanów można rozmieścić bezkonfliktowo na planszy 27×27 na 234 907 967 154 122 528 (blisko 235 biliardów) sposobów, z czego całkowicie różnych jest prawie ośmiokrotnie mniej - 29 363 495 934 315 694. Na wynik dla n=28 przyjdzie zapewne poczekać, aż do akcji wkroczą komputery kwantowe.
W lipcu 2021 roku izraelski matematyk Michael Simkin (11), pracownik naukowy Center of Mathematical Sciences and Applications na Uniwersytecie Harvarda, obliczył, bez wykorzystania symulacji komputerowej, że jest około (0,143n)n sposobów rozmieszczenia hetmanów, aby żadne nie atakowały się na szachownicach n×n. Należy jednak pamiętać, że jest to jedynie przybliżony wynik.
Wartość wynikająca ze wzoru Simkina jest tym bliższa rzeczywistej, im większe jest n, jednak zbliżanie się jest bardzo wolne, więc dla kilku-, a nawet kilkunastocyfrowych n wynik obarczony jest znacznym błędem. Na szachownicy o wymiarach 1 000 000 na 1 000 000 liczba sposobów na ułożenie królowych tak, aby wzajemnie się nie atakowały wynosi 1 i… około pięciu milionów zer.
Problem dominacji 4 hetmanów
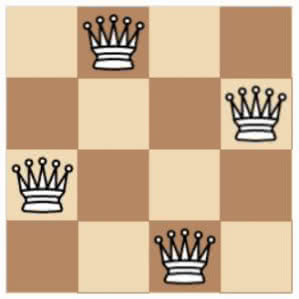
Na szachownicy 8×8 należy rozstawić 4 hetmany tak, aby jak najwięcej pól było atakowanych. Okazuje się, że siła czterech hetmanów nie jest wystarczająca do opanowania całej planszy, zawsze co najmniej dwa pola pozostają nieatakowane.
Jest 8 ustawień (nie licząc wariantów, które można otrzymać za pomocą obrotów i odbić zwierciadlanych), przy których tylko dwa pola są nieatakowane.
Na przykład na diagramie 12 jedyne pola nieszachowane to c3 i d2.
Biorąc pod uwagę planszę n×n, liczba dominacji to minimalna liczba hetmanów (lub innych figur) potrzebnych do zaatakowania lub zajęcia każdego pola. Dla n=8 liczba dominacji hetmana wynosi 5.
dr inż. Jan Sobótka