Kwanty dla bezpieczeństwa komputerowego - ostatnia deska ratunku czy gwóźdź do trumny? Gdy będziemy mieć miliony kubitów
Kilka miesięcy temu w "Applied Physics Letters" naukowcy z Chin zaprezentowali najszybszy jak dotąd kwantowy generator liczb losowych (ang. Quantum Random Number Generator, QRNG) działający w czasie rzeczywistym. Dlaczego to ważne? Bo zdolność do generowania (prawdziwych) liczb losowych jest kluczowa w szyfrowaniu.
Większość systemów QRNG wykorzystuje dziś dyskretne komponenty fotoniczne i elektroniczne, ale integracja takich komponentów w ramach układu scalonego pozostaje sporym wyzwaniem technicznym. Układ opracowany przez grupę wykorzystuje fotodiody indowo-germanowe i wzmacniacz transimpedancyjny zintegrowany z krzemowym układem fotonicznym (1), który zawiera układ sprzęgaczy i tłumików.
Połączenie tych komponentów pozwala QRNG na wykrywanie sygnałów ze źródła entropii kwantowej ze znacznie poprawioną odpowiedzią częstotliwościową. Po wykryciu losowych sygnałów są one przetwarzane przez programowalną tablicę bramek, która wyodrębnia prawdziwie losowe liczby z surowych danych. Powstałe w ten sposób urządzenie może generować liczby z prędkością prawie 19 gigabitów na sekundę, co jest nowym rekordem świata. Liczby losowe mogą być następnie przesłane do dowolnego komputera za pomocą kabla światłowodowego.
Kwantowe generowanie liczb losowych ma fundamentalne znaczenie dla kryptografii. Konwencjonalne generatory liczb losowych zazwyczaj opierają się na algorytmach znanych jako generatory liczb pseudolosowych, które, jak sama nazwa wskazuje, nie są prawdziwie losowe, a zatem potencjalnie podatne na złamanie. Nad optycznymi kwantowymi generatorami liczb prawdziwie losowych pracują m.in. takie firmy jak Quantum Dice i IDQuantique. Ich produkty są już wykorzystywane w celach komercyjnych.
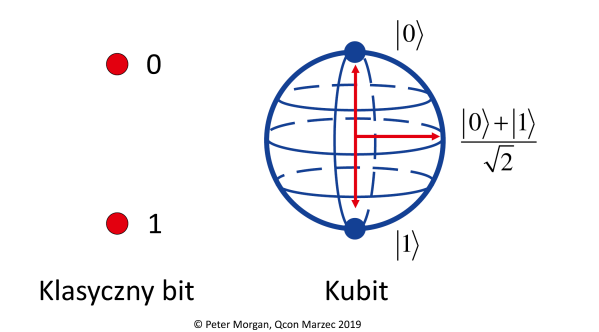
Obliczenia kwantowe opierają się na mechanice kwantowej, która reguluje sposób działania obiektów fizycznych w najmniejszych skalach. Kwantowym odpowiednikiem bitu 1 lub 0 jest kubit (2), który również może mieć wartość 0 lub 1 albo też znajdować się w tak zwanej superpozycji - dowolnej kombinacji 0 i 1. Wykonanie obliczenia na dwóch klasycznych bitach (które mogą mieć wartości 00, 01, 10 i 11) wymaga wykonania czterech działań.
Komputer kwantowy może wykonywać obliczenia na wszystkich czterech stanach jednocześnie. Skaluje się to wykładniczo - tysiąc kubitów byłoby, pod pewnymi względami, potężniejsze niż najpotężniejszy superkomputer na świecie. Inną koncepcją kwantową kluczową dla obliczeń kwantowych jest splątanie, dzięki któremu kubity mogą zostać skorelowane w taki sposób, że są opisywane przez jeden stan kwantowy. Zmierzenie jednego z nich natychmiast ujawnia stan drugiego.
Splątanie jest ważne w kryptografii i komunikacji kwantowej. Potencjał obliczeń kwantowych nie polega jednak na przyspieszeniu obliczeń. Zapewnia raczej wykładniczą przewagę w pewnych klasach problemów, takich jak obliczanie bardzo dużych liczb, co będzie miało głębokie implikacje dla bezpieczeństwa cybernetycznego.
Najpilniejszym wyzwaniem informatyki kwantowej jest osiągnięcie wystarczającej liczby odpornych na błędy kubitów, aby uwolnić potencjał obliczeń kwantowych. Kubity są z natury niestabilne. Interakcja pomiędzy kubitem a jego otoczeniem powoduje degradację informacji w ciągu mikrosekund. Odizolowanie kubitów od otoczenia, na przykład przez schłodzenie ich do temperatury bliskiej zera absolutnego, jest trudne i kosztowne. Szum rośnie wraz z liczbą kubitów, co wymaga zastosowania złożonych metod korekcji błędów.
Komputery kwantowe są obecnie programowane z pojedynczych kwantowych bramek logicznych, co może być akceptowane w małych, prototypowych komputerach kwantowych, ale jest niepraktyczne, gdy dojdziemy do tysięcy kubitów. Od niedawna niektóre firmy, np. IBM i Classiq, opracowują bardziej abstrakcyjne warstwy w stosie programowania, umożliwiając programistom tworzenie potężnych aplikacji kwantowych do rozwiązywania rzeczywistych problemów.
Specjaliści uważają, że podmioty o złych intencjach mogą wykorzystać zalety obliczeń kwantowych do stworzenia nowego podejścia w naruszeniach bezpieczeństwa cybernetycznego. Mogą podejmować działania, które byłyby zbyt kosztowne obliczeniowo na klasycznych komputerach. Dzięki komputerowi kwantowemu haker może w teorii szybko przeanalizować zbiory danych i przystąpić do przeprowadzenia wyrafinowanego ataku na dużą populację sieci i urządzeń.
Choć w tej chwili wydaje się mało prawdopodobne, że hakerzy będą mieli zasoby do rozwijania swoich systemów obliczeń kwantowych, to przy obecnym tempie postępu technologicznego pojawienie się obliczeń kwantowych ogólnego przeznaczenia będzie wkrótce dostępne w chmurze jako platforma typu infrastruktura-jako-usługa, co sprawi, że będą one dostępne dla szerokiego grona użytkowników.
Już w 2019 roku Microsoft ogłosił, że będzie oferował obliczenia kwantowe w swojej chmurze Azure, choć ograniczy ich wykorzystanie do wybranych klientów. W ramach tego produktu firma zapewnia rozwiązania kwantowe, takie jak solwery i algorytmy, oprogramowanie kwantowe, takie jak symulatory i narzędzia do szacowania zasobów, oraz sprzęt kwantowy z różnymi architekturami kubitów, z których wszystkie potencjalnie mogą być wykorzystywane przez hakerów. Innymi dostawcami usług przetwarzania kwantowego w chmurze są IBM i Amazon Web Services (AWS).
Zmagania algorytmów
Klasyczne szyfry cyfrowe opierają się na skomplikowanych formułach matematycznych w celu przekształcenia danych w zaszyfrowane wiadomości do przechowywania i przesyłania. Do szyfrowania i odszyfrowywania danych używany jest klucz cyfrowy.
W związku z tym atakujący próbuje złamać metodę szyfrowania, aby ukraść lub zmodyfikować chronione informacje. Oczywistym sposobem na to jest wypróbowanie wszystkich możliwych kluczy w celu zidentyfikowania tego, który odszyfruje dane z powrotem do czytelnej postaci. Proces ten może być przeprowadzony przy użyciu konwencjonalnego komputera, ale wymaga ogromnego wysiłku i czasu.
Obecnie istnieją dwa główne typy szyfrowania: symetryczne, w którym ten sam klucz jest używany do szyfrowania i odszyfrowywania danych; oraz asymetryczne, czyli z kluczem publicznym, które obejmuje parę matematycznie powiązanych kluczy, jeden udostępniany publicznie, aby umożliwić ludziom szyfrowanie wiadomości dla właściciela pary kluczy, a drugi przechowywany prywatnie przez właściciela w celu odszyfrowania wiadomości.
W szyfrowaniu symetrycznym ten sam klucz jest używany do szyfrowania i deszyfrowania danego fragmentu danych. Przykładem algorytmu symetrycznego jest Advanced Encryption Standard (AES). Algorytm AES, przyjęty przez rząd USA, obsługuje trzy rozmiary kluczy: 128 bitów, 192 bity i 256 bitów. Algorytmy symetryczne są zwykle używane do masowych zadań szyfrowania, takich jak szyfrowanie dużych baz danych, systemów plików i pamięci obiektowych.
W szyfrowaniu asymetrycznym dane są szyfrowane przy użyciu jednego klucza (zwykle określanego jako klucz publiczny) i odszyfrowywane przy użyciu innego klucza (zwykle określanego jako klucz prywatny). Powszechnie stosowany algorytm Rivesta, Shamira, Adlemana (RSA) jest przykładem algorytmu asymetrycznego. Mimo że działają wolniej niż szyfrowanie symetryczne, algorytmy asymetryczne rozwiązują problem dystrybucji klucza, który jest ważnym zagadnieniem w szyfrowaniu.
Kryptografia klucza publicznego jest używana do bezpiecznej wymiany kluczy symetrycznych oraz do cyfrowego uwierzytelniania - lub podpisywania - wiadomości, dokumentów i certyfikatów, które łączą klucze publiczne z tożsamością ich właścicieli. Gdy odwiedzamy bezpieczną witrynę internetową, która używa protokołów HTTPS, nasza przeglądarka używa kryptografii klucza publicznego do uwierzytelnienia certyfikatu witryny i skonfigurowania klucza symetrycznego do szyfrowania komunikacji do i z witryny.
Ponieważ praktycznie wszystkie aplikacje internetowe używają zarówno kryptografii symetrycznej, jak i kryptografii klucza publicznego, obie formy muszą być bezpieczne. Najprostszym sposobem złamania kodu jest wypróbowanie wszystkich możliwych kluczy, aż do uzyskania tego, który działa. Konwencjonalne komputery potrafią to zrobić, ale jest to bardzo trudne.
Na przykład w lipcu 2002 r. pewna grupa ogłosiła, że odkryła symetryczny klucz 64-bitowy, ale potrzebowała wysiłku 300 tys. osób przez ponad cztery i pół roku pracy. Klucz o dwukrotnie większej długości, czyli 128 bitów, miałby ponad 300 sekstylionów rozwiązań, czyli liczby wyrażonej przez 3, po którym następuje 38 zer. Nawet najszybszy superkomputer na świecie potrzebowałby trylionów lat na znalezienie właściwego klucza. Metoda obliczeń kwantowych, zwana algorytmem Grovera, przyspiesza jednak ten proces, zamieniając 128-bitowy klucz w kwantowo-komputerowy odpowiednik klucza 64-bitowego. Obrona jest jednak prosta - należy wydłużyć klucze. Na przykład klucz 256-bitowy ma takie samo zabezpieczenie przed atakiem kwantowym, jak klucz 128-bitowy przed atakiem konwencjonalnym.
Kryptografia z kluczem publicznym stanowi jednak o wiele większy problem ze względu na sposób działania matematyki. Popularne obecnie algorytmy szyfrowania z kluczem publicznym, nazywane RSA, Diffiego-Hellmana i kryptografia krzywych eliptycznych, umożliwiają rozpoczęcie od klucza publicznego i matematyczne obliczenie klucza prywatnego bez wypróbowywania wszystkich możliwości.
Przyszłe komputery kwantowe mogą umieć złamać rozwiązania szyfrowania, które opierają swoje zabezpieczenia na faktoryzacji liczb całkowitych lub logarytmach dyskretnych. W przypadku powszechnie stosowanej w e-commerce metody RSA, na przykład klucz prywatny można obliczyć poprzez faktoryzację liczbę, która jest iloczynem dwóch liczb pierwszych, tak jak 3 i 5 dla 15. Do tej pory szyfrowanie z użyciem klucza publicznego było nie do złamania. Badania przeprowadzone przez Petera Shora na MIT ponad 20 lat temu wykazały, że złamanie szyfrowania asymetrycznego jest możliwe.
Wystarczająco zaawansowane komputery kwantowe mogłyby złamać nawet 4096-bitowe pary kluczy w ciągu zaledwie kilku godzin, stosując metodę zwaną algorytmem Shora. To jednak dotyczy idealnych komputerów kwantowych przyszłości. Jak dotąd największa liczba obliczona na komputerze kwantowym to 15 - zaledwie 4 bity.
Chociaż algorytmy symetryczne nie są zagrożone przez algorytm Shora, moc obliczeń kwantowych wymusza zwielokrotnienie rozmiarów kluczy. Na przykład duże komputery kwantowe działające według algorytmu Grovera, który wykorzystuje metody kwantowe do bardzo szybkiego przeszukiwania baz danych, mogłyby zapewnić czterokrotną poprawę wydajności w atakach typu brute force na symetryczne algorytmy szyfrujące, takie jak AES. Aby odeprzeć ataki typu brute force, należy podwoić rozmiar klucza, aby zapewnić ten sam poziom ochrony. W przypadku algorytmu AES oznacza to stosowanie 256-bitowych kluczy, aby zachować dzisiejszą 128-bitową siłę zabezpieczeń.
Dzisiejsze szyfrowanie RSA, powszechnie stosowana forma szyfrowania, szczególnie w przypadku przesyłania poufnych danych przez Internet opiera się na liczbach 2048-bitowych. Eksperci szacują, że komputer kwantowy musiałby mieć aż 70 milionów kubitów, aby złamać to szyfrowanie. Biorąc pod uwagę, że obecnie największe komputery kwantowym mają nie więcej niż sto kubitów (choć IBM i Google mają plany osiągnięcia miliona do 2030 r.), może minąć sporo czasu, zanim pojawi się rzeczywiste zagrożenie Ponieważ jednak tempo badań w tej dziedzinie stale przyspiesza, nie można wykluczyć, że taki komputer powstanie w ciągu najbliższych 3-5 lat.
Przykładowo Google i Instytut KTH w Szwecji podobno znalazły niedawno "bardziej wydajny sposób", za pomocą którego komputery kwantowe mogą wykonywać obliczenia związane z łamaniem kodów, zmniejszając zasoby, których potrzebują, o rzędy wielkości. Ich praca, opisana w "MIT Technology Review", głosi, że komputer o mocy 20 milionów kubitów jest w stanie złamać 2048-bitową liczbę w ciągu zaledwie 8 godzin.
Kryptografia postkwantowa
W ciągu ostatnich kilku lat naukowcy ciężko pracowali nad stworzeniem szyfrowania "bezpiecznego kwantowo". "American Scientist" donosi, że amerykański Narodowy Instytut Standardów i Technologii (NIST) jest już w trakcie analizy 69 potencjalnych nowych metod nazywanych "kryptografią postkwantową (PQC)". Jednak to samo pismo zaznacza, że kwestia złamania współczesnej kryptografii przez komputery kwantowe pozostaje wciąż w sferze hipotetycznej.
Tak czy inaczej, według raportu National Academies of Sciences, Engineering, and Medicine z 2018 roku, "nowa kryptografia musi zostać opracowana i wdrożona już teraz, nawet jeśli komputer kwantowy, który mógłby złamać dzisiejszą kryptografię, powstanie dopiero za dekadę". Przyszłe komputery kwantowe łamiące kody mogą mieć sto tysięcy razy większą moc obliczeniową i obniżony poziom błędów, co czyni je zdolnymi do walki nowoczesnymi technikami cyberbezpieczeństwa.
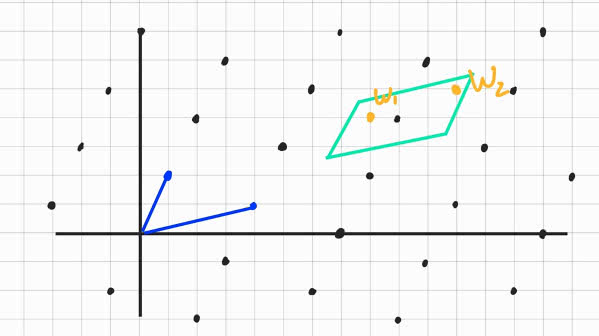
Z rozwiązań zwanych "postkwantową kryptografią" znana jest m.in. firma PQShield. Specjaliści ds. bezpieczeństwa mogą zastąpić konwencjonalne algorytmy kryptograficzne algorytmami opartymi na siatce (Lattice-Based Cryptography), które zostały stworzone z myślą o bezpieczeństwie. Te nowe metody ukrywają dane wewnątrz złożonych problemów matematycznych zwanych kratami (3). Takie struktury algebraiczne są trudne do rozwiązania, dzięki czemu kryptografowie mogą chronić informacje nawet w obliczu silnych komputerów kwantowych.
Według badaczki z IBM, Cecilii Boschini, kryptografia oparta na siatkach będzie w przyszłości udaremniać ataki oparte na komputerach kwantowych, a także stanowić podstawę dla szyfrowania w pełni homomorficznego (Fully Homomorphic Encryption, FHE), które umożliwia użytkownikom wykonywanie obliczeń na pliku bez oglądania danych lub ujawniania ich hakerom.
Inną obiecującą metodą jest dystrybucja klucza kwantowego (QKD). Kwantowa dystrybucja kluczy QKD (4) wykorzystuje zjawiska mechaniki kwantowej (takie jak splątanie), aby umożliwić całkowicie tajną wymianę kluczy szyfrujących, a nawet może ostrzegać o obecności "podsłuchiwacza" między dwoma punktami końcowymi.
Początkowo metoda ta była możliwa tylko przez światłowód, ale firma Quantum Xchange opracowała teraz sposób na przesyłanie jej również przez Internet. Znane są, na przykład chińskie, eksperymenty QKD przez satelitę na odległość kilku tysięcy kilometrów. Poza Chinami pionierami w tej dziedzinie są firmy KETS Quantum Security i Toshiba.
Mirosław Usidus