Piąty wymiar ciemnej materii w nieznanym stanie skupienia. Informacja-kwanty-rzeczywistość-świadomość

Zaproponowana w 2019 r. przez Melvina Vopsona, fizyka z Uniwersytetu z Portsmouth w Wielkiej Brytanii zasada równoważności masa-energia-informacja (M/E/I), według której masa może być wyrażona jako energia lub informacja lub odwrotnie, zakłada, że bity informacji muszą mieć pewną niewielką masę. Uczony twierdzi, że informacja jest piątą formą materii we Wszechświecie.
Jego hipotezy, których trafność sprawdzana jest eksperymentalnie, należą do narastającej w fizyce fali badań nad informacją, która miałaby być w niektórych teoriach nie tyle nawet równoważnikiem masy czy energii lecz czymś od nich nawet bardziej podstawowym, zasadą, która miałaby leżeć głębiej, podłoża wszystkiego w znanym nam Wszechświecie, a może nawet poza nim. Tak się jednocześnie składa, że temat "informacyjny" a nawet, powiedzmy "informatyczny" w fizyce w 2022 roku powrócił z hukiem, gdyż ubiegłoroczni Nobliści krążyli w swoich nagrodzonych badaniach eksperymentach wokół kwestii informacji w mechanice kwantowej.
Upiorne działanie
Laureatami Nagrody Nobla z fizyki w 2022 roku byli Alain Aspect, John Clauser i Anton Zeilinger (1). Nagroda została przyznana "za eksperymenty ze splątanymi fotonami, ustalenie naruszenia nierówności Bella i pionierskie odkrycia w dziedzinie informatyki kwantowej". Ich prace miały kluczowe znaczenie dla dziedziny zwanej współcześnie kwantową teorią informacji, która obejmuje kwestie związane z budową komputerów kwantowych, kwantową kryptografię i teleportację.
Szczególnie ważne w rozwoju tego nurtu były badania irlandzkiego fizyka Johna Bella (2). W latach 60. XX wieku Bell opracował twierdzenie zwane też nierównością Bella. W skrócie jest to formułowane w ten sposób: "żadna lokalna teoria zmiennych ukrytych nie może opisać wszystkich zjawisk mechaniki kwantowej". Brzmi niewinnie, ale był to potężny cios w serce fizyki, które krwawiło z powodu paradoksów kwantowych już od kilku dekad wcześniej.
W pierwszych dekadach XX wieku fizycy byli podzieleni w kwestii interpretacji mechaniki kwantowej. Wśród tych, którzy uważali, że świat kwantowy jest zasadniczo odmienny od znanych teorii, byli m.in. Werner Heisenberg i Niels Bohr. W obozie naukowców, którzy uważali, że świat kwantowy musi być taki jak zwykły świat, tylko na razie nie możemy tego klasycznie wyjaśnić, byli Albert Einstein i Erwin Schrödinger. U podstaw tego podziału znajduje się jedno z przewidywań teorii kwantowej dotyczące splątania stanów kwantowych i w konsekwencji czegoś co Einstein określił jako "upiorne oddziaływanie na odległość".
W 1935 roku Einstein wraz z dwoma kolegami opracował eksperyment myślowy, który pokazał, że mechanika kwantowa nie daje nam całej wiedzy o splątaniu. Uważali, że musi być coś więcej, czego jeszcze nie możemy zobaczyć. Wszystko to było jednak traktowane jako coś w rodzaju problemu filozoficznego a nie przedmiot badań fizycznych. Dopiero w latach sześćdziesiątych wspominany Bell wykazał, że nie ma możliwości, aby opis kwantowy był niekompletny przy jednoczesnym zakazie "upiornego działania na odległość" i nadal odpowiadał przewidywaniom teorii kwantowej. Nie była to jednak jeszcze wygrana przeciwników Einsteina. W latach 60. nie było bowiem wciąż oczywiste, czy przewidywania teorii kwantowej są rzeczywiście poprawne. Aby naprawdę udowodnić twierdzenie Bella, ktoś musiał poddać ten wywód eksperymentalnej próbie.
I tu do historii wkraczają dwaj tegoroczni laureaci Nagrody Nobla. Najpierw John Clauser, a potem Alain Aspect, przeprowadzili eksperymenty na proponowanym przez Bella układzie. Ostatecznie wykazały one, że przewidywania mechaniki kwantowej są dokładne. W rezultacie, o ile nie przyjmiemy "upiornego działania na odległość", nie istnieje żaden układ splątanych układów kwantowych, który mógłby opisać obserwowany świat kwantowy. Inaczej rzecz ujmując, wydaje się, że nie chodzi o to, że świat kwantowy jest taki sam jak znany nam świat a my po prostu nie umiemy go opisać. Jak to ujął trzeci tegoroczny laureat Nagrody Nobla, Anton Zeilinger, "rozróżnienie między rzeczywistością a naszą wiedzą o niej, czyli między rzeczywistością a informacją, jest niewykonalne". Nie ma możliwości odniesienia się do rzeczywistości bez użycia informacji, które o niej posiadamy.
Jak teoria informacji spotkała się z mechaniką kwantową
Od czasu powstania teorii informacji w 1948 roku, kiedy to Claude Shannon (3) opublikował wraz Warrenem Weaverem pracę zatytułowaną "A Mathematical Theory of Communication", rozbudowuje się jej powiązania z wieloma dziedzinami, w tym oczywiście z fizyką, ostatnio głównie mechaniką kwantową. Powiązania a nie proste przekładanie jednej teorii na drugą, gdyż w rzeczywistości kwantowa teoria informacji ma konsekwencje, które nie mają wiele wspólnego z klasyczną wersją teorii informacji. Niemniej zapewnia ona logiczną strukturę pozwalającą na wprowadzenie idei kwantowej teorii informacji. Michał Horodecki, polski fizyk pisał, że koncepcja informacji kwantowej zrodziła się na pograniczu dwóch dziedzin - mechaniki kwantowej i nauk o informacji, za których "ojca" uważa się Shannona.
Teoria informacji opiera się na teorii prawdopodobieństwa i statystyce, często zajmując się miarami informacji rozkładów związanych ze zmiennymi losowymi. Jedną z najważniejszych miar jest entropia, która stanowi budulec wielu innych miar. Entropia określa miarę niepewności związanej z wartością zmiennej losowej lub wynikiem procesu losowego. Na przykład, określenie wyniku rzutu monetą (z dwoma równie prawdopodobnymi wynikami) dostarcza mniej informacji (niższa entropia) niż określenie wyniku rzutu kostką (z sześcioma równie prawdopodobnymi wynikami). Duża część matematyki stojącej za teorią informacji o zdarzeniach o różnym prawdopodobieństwie została opracowana w dziedzinie termodynamiki przez Ludwiga Boltzmanna i J. Willarda Gibbsa. Widać więc związki między entropią w teorii informacji a entropią termodynamiczną. Wspomniany prof. Horodecki uważa nawet, iż entropia przestrzeni fazowej Gibbsa w termodynamice klasycznej jest szczególnym przypadkiem entropii Shannona.
W latach 60. XX wieku Rusłan Stratonovich, Carl Helstrom i James P. Gordon zaproponowali komunikację optyczną z wykorzystaniem mechaniki kwantowej. Było to pierwsze historyczne pojawienie się kwantowej teorii informacji. Badali oni głównie prawdopodobieństwa błędów i pojemności kanałów dla komunikacji. Nieco później Alexander Holevo uzyskał górną granicę szybkości komunikacji w przesyłaniu klasycznej wiadomości przez kanał kwantowy. Za pierwszego uczonego, który użył terminu "kwantowa teoria informacji" uważa się Polaka, prof. Romana Ingardena z Instytutu Fizyki Uniwersytetu Mikołaja Kopernika w Toruniu. W 1975 opublikował pracę "Quantum Information Theory", która w sposób pionierski prezentowała zarys systematycznej konstrukcji kwantowej teorii informacji.
W 1995 roku Ben Schumacher ukuł słowo kubit (4), (czyli kwantowa cyfra binarna), aby reprezentować podstawową jednostkę informacji kwantowej, i udowodnił, że optymalna szybkość kompresji danych dla kwantowego źródła informacji jest dana przez kwantowe pojęcie entropii, tzw. entropię von Neumanna. Pod koniec XX wieku przeprowadzono pierwsze eksperymenty z użyciem obiektów kwantowych, takich jak np. fotony, do zapisywania i przesyłania informacji. Doświadczenia te otworzyły drogę do opracowania nowych kwantowych technologii komunikacyjnych. Obecnie jest to jedna z najpopularniejszych i najdynamiczniej rozwijających się gałęzi fizyki.
W komputerach kwantowych nie ma copy-paste
Współczesne komputery działają według reguł fizyki klasycznej. Obwody elektroniczne stają się jednak, wraz postępami miniaturyzacji, tak małe, że będzie można w nich zauważyć efekty charakterystyczne dla świata kwantowego. Sam proces miniaturyzacji skłania nas do zmiany reguł gry, z klasycznych na kwantowe.
Kwantowa informacja charakteryzuje się wieloma nieintuicyjnymi cechami, np. ogólnie rzecz biorąc, nie można jej kopiować, klonować, tak jak klasycznej informacji. Zakaz klonowania jest fundamentalnym prawem kwantowej teorii informacji, ma bardzo szerokie implikacje. W szczególności oznacza on, że informacji kwantowej nie można wzmacniać. Wynika stąd jeden z najtrudniejszych problemów tej dziedziny - ochrona informacji kwantowej przed dekoherencją.
Od niedawna również wiadomo, że informacja kwantowa może być ujemna, co jest szczególnie zaskakujące, bo zazwyczaj spodziewamy się, że układ po otrzymaniu porcji informacji będzie zawierał jej więcej. Jednak najbardziej niezwykłą z klasycznego, ludzkiego punktu widzenia, a przy tym potencjalnie bardzo użyteczną cechą stanów kwantowych jako nośników kwantowej informacji jest możliwość tworzenia z nich superpozycji stanów.
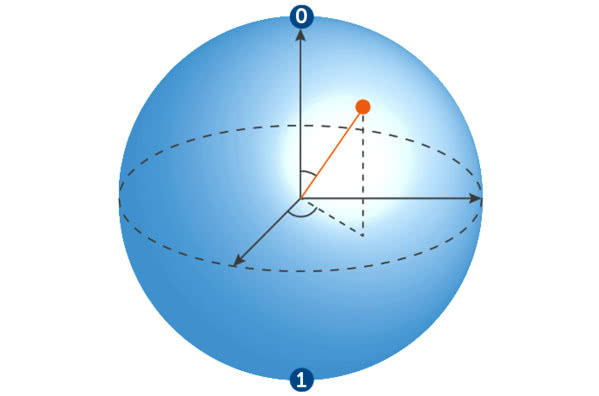
Współczesne komputery operują na klasycznych bitach, które w danym momencie mogą się znajdować tylko w jednym z dwóch stanów, umownie nazywanych "0" i "1". Bity kwantowe mogą istnieć w dowolnej mieszaninie (superpozycji) stanów i dopiero przy odczytywaniu przez nas wartości przyjmują wartość "0" lub "1". Różnicę widać wraz ze wzrostem ilości przetwarzanej informacji. Klasyczny komputer, operujący na 10 bitach, w jednym kroku może przetwarzać tylko jeden z 1024 (210) stanów takiego rejestru, zaś komputer operujący na bitach kwantowych przetworzyłby je wszystkie w jednym kroku. Zwiększenie liczby bitów kwantowych do np. stu otwierałoby możliwość przetworzenia w pojedynczym cyklu więcej niż tysiąca miliardów miliardów miliardów stanów. Komputer operujący na dostatecznie wielu bitach kwantowych mógłby więc w niezwykle krótkim czasie realizować kwantowe algorytmy przetwarzania danych, np. dotyczące rozkładu wielkich liczb naturalnych na czynniki pierwsze. Zamiast po milionach lat obliczeń, wynik byłby gotowy po upływie zaledwie godzin lub nawet minut.
Pomijając problemy z budową układów, dekoherencją bitów (kubitów), oraz spór, czy rzeczywiście udało nam się zbudować jakikolwiek komputer kwantowy, uznaje się, że informacja, a może raczej informatyka, kwantowa znalazła już pierwsze zastosowania komercyjne. Od kilku lat na rynku są dostępne urządzenia do kryptografii kwantowej, metody szyfrowania danych, w której kwantowe prawa przetwarzania informacji gwarantują całkowite bezpieczeństwo. Na razie kwantowe szyfrowanie stosują niektóre banki, w przyszłości technologia z pewnością stanieje i pozwoli np. na realizację całkowicie bezpiecznych transakcji bankomatowych lub połączeń internetowych.
Tematyka informacji kwantowej to nie tylko kubity i zagadnienia ich stabilności. Wkracza ona, także przez fizykę do świata biologii i badań nad umysłem i świadomością. Sprawcami są sami fizycy. Erwin Schrödinger, który w swojej opublikowanej w 1944 roku pracy pt. "Czym jest życie?" zauważał, że życie wydaje się zaskakujące w świetle praw fizyki. W zamkniętych systemach fizycznych entropia wzrasta z czasem. W systemach żywych jest, jak oceniał Schrödinger, jest inaczej - z czasem porządek i złożoność wzrastają. Wielki fizyk sądził, że wyjaśnienie tego paradoksu można znaleźć poprzez wyjaśnienie mechanizmu replikacji życia. Pisał o czymś, co nazwał "substancją dziedziczną".
Wkrótce po ukazaniu się rozważań Schrödingera James Watson i Francis Crick odkryli strukturę podwójnej helisy DNA. W swojej drugiej pracy pt. "Genetical Implications of the Structure of Deoxyribonucleic Acid", zauważają, że materiał dziedziczny wydaje się również przekazywać informacje. Język teorii informacji został wprowadzony genetyki i badań nad powstaniem życia. Freeman Dyson, fizyk, który w swojej książce z 1999 r. - "Origins of Life" pisał o roli metabolizmu i replikacji ewolucji życia organizmów orzekł, że powstanie życia jest powstaniem systemu przetwarzania informacji. Obecnie pogląd, że określenie mechanizmów oddziaływania informacji z materią stanowi klucz do rozwiązania zagadki życia.
Niektórzy uważają, że nie tylko życia, ale jego najwyższego, jak się wydaje, przejawu, który nazywamy "świadomością". Wielu naukowców obawia się, że hipotezy na temat kwantowej natury umysłu i pamięci należą do mającej opinię pozanaukowej, dziedziny. Z drugiej strony czymże jak nie nauką jest poszukiwanie fizycznego, choć kwantowego, podłoża dla świadomości.
Anestezjolog z amerykańskiej Arizony, Stuart Hameroff, twierdzi już od wielu lat, że mikrotubule, włókniste struktury o średnicy 20-27 nm, powstające w wyniku polimeryzacji białka tubuliny, a pełniące funkcję cytoszkieletu nadającego kształt komórce, w tym także komórce nerwowej, wchodzą w "superpozycje" w rozumieniu mechaniki kwantowej, co pozwala im mieć dwa różne kształty jednocześnie. Każdy z owych kształtów wiąże się z określoną ilością informacji. Według tego poglądu są kubitami, przechowującymi dwukrotnie więcej danych niż wynikałoby to z klasycznego rozumienia układu. Jeśli dodamy do tego zjawisko splątania kubitów, czyli oddziaływania cząstek niebędących w bezpośrednim sąsiedztwie, to rysuje się model funkcjonowania mózgu jako kwantowego komputera, który opisywał słynny fizyk Roger Penrose. Hameroff nawiązał zresztą z nim współpracę, tłumacząc niezwykłą szybkość, elastyczność i wszechstronność mózgu właśnie tym, że jest to kwantowy komputer.
Z hipotez na temat kwantowego podłoża świadomości wynikają interesujące konsekwencje dla perspektyw rozwoju sztucznej inteligencji. Zgodnie z nimi prawdziwie świadomej AI nie mamy szans zbudować na bazie klasycznej, opartej na krzemie i tranzystorach technologii. Dopiero komputery kwantowe - i to nie te obecnej ani nawet kolejnej generacji - otworzą drogę do "prawdziwego", czyli świadomego, syntetycznego mózgu.
Niektórzy naukowcy postanowili to sprawdzić eksperymentalnie hipotezy Hameroffa i Penrose’a. Biologiczna wykonalność tego co proponują, jest sprawdzana w ostatnich badaniach eksperymentalnych nad dynamiką mikrotubul. Wykazano w nich, że struktury te nie posiadają właściwości wymaganych do utrzymania propozycji Orch-OR (tak w skrócie określa się teorię Hameroffa i Penrose’a).
Badane są też inne możliwości, teoretyczne "nośniki" kubitów w biologicznych strukturach. Spośród projektów badawczych wyróżnia się przedsięwzięcie specjalistów z Uniwersytetu Kalifornijskiego w Santa Barbara. Próbują sprawdzić, czy kubity mogą być przechowywane w jądrach atomowych. Zainteresowanie fizyków budzą w szczególności atomy fosforu, którego w ludzkich organizmach nie brakuje.
Jego jądra mogłyby odgrywać rolę kubitów biochemicznych. Kolejny eksperyment ma na celu zbadanie mitochondriów, podjednostek komórek odpowiedzialnych za metabolizm i przekaz informacji w organizmie - czy nie odgrywają też roli w splątaniu i generowaniu kubitów informacji.
Być może właściwym tropem są tzw. biofotony. Kilka miesięcy temu naukowcy z Uniwersytetu w Calgary odkryli, że neurony w mózgach ssaków są zdolne do produkcji fotonów światła. Ożywiło to spekulacje, czy w naszym mózgu oprócz znanych od dawna sygnałów w sieni neuronowej funkcjonują także optyczne kanały komunikacji. Biofotony produkowane przez mózg mogą być z powodzeniem splątane kwantowo. Biorąc pod uwagę liczbę neuronów w ludzkim mózgu, w ciągu jednej sekundy mógłby w nim być emitowany nawet miliard biofotonów. Przy uwzględnieniu efektów splątania daje to gigantyczne ilości informacji przetwarzanej w hipotetycznym fotonowym biokomputerze.
Zerojedynkowość rzeczywistości
Znaczenie informacji jako niejako "podłoża" znanej nam fizycznej rzeczywistości podkreśla model binarny Wszechświata, o którym pisał w liście do "Młodego Technika" kilka miesięcy temu Mariusz Stanowski, autor książki "Theory and Practice of Contrast Integrating Science, Art and Philosophy", w której ta hipoteza jest przedstawiona bliżej.
Binarność (zerojedynkowość), z którą w naszej cyfrowej erze informacji jesteśmy oswojeni, przenika w tym modelu wszystko (5). Od najgłębszego podłoża - cząstki mają przeciwne ładunki, dodatni i ujemny, są cząstkami lub antycząstkami, spin cząstek jest albo zgodny z ruchem wskazówek zegara albo przeciwny. Natura jest binarna w swojej fizycznej strukturze materii i energii, wyewoluowała i istnieje w postaci elementów binarnych.
Stanowski pisze w swojej książce, że rzeczywistość jako stale rosnącą liczbą binarną, która składa się z elementów (impulsów i odstępów czasowych), które następują po sobie w określonym porządku. Liczba taka charakteryzuje się jedynie wymiarem czasowym. Dla umysłu jest to trudne do uchwycenia, ponieważ aby to zrobić, musielibyśmy zapamiętać kolejność wszystkich elementów i dotrzeć do każdego z nich w odpowiedniej kolejności, jak w przypadku nagrania na taśmie. To wyjaśnia, dlaczego nasz umysł generuje wymiar przestrzennoliniowy, który ułatwia mu dostęp do wszystkich elementów liczby. Taką generalizacją jest drugi i trzeci wymiar, które ułatwiają nam postrzeganie bardziej złożonej rzeczywistości. Dodawanie przez nasz umysł kolejnych wymiarów wiąże się ze wzrostem liczby wykorzystywanych przez nas elementów informacji i koniecznością ich kompresji. Przestrzeń trójwymiarowa (widzenie przestrzenne) reprezentuje właśnie taką kompresję (organizację) informacji. Kompresja informacji polega na zapisaniu określonej liczby elementów informacji przy użyciu mniejszej liczby bitów, czyli mniejszej energii. Z tej definicji wynika, że przestrzeń należy traktować nie jako kategorię fizyczną, ale mentalną.
W rozumowaniu tym dochodzimy do konkluzji, że człowiek to binarna struktura rzeczywistości o dużej złożoności. Umysł to binarna struktura największej znanej nam złożoności. Wszystko jest informacją - informacja jest wszystkim.
Mirosław Usidus