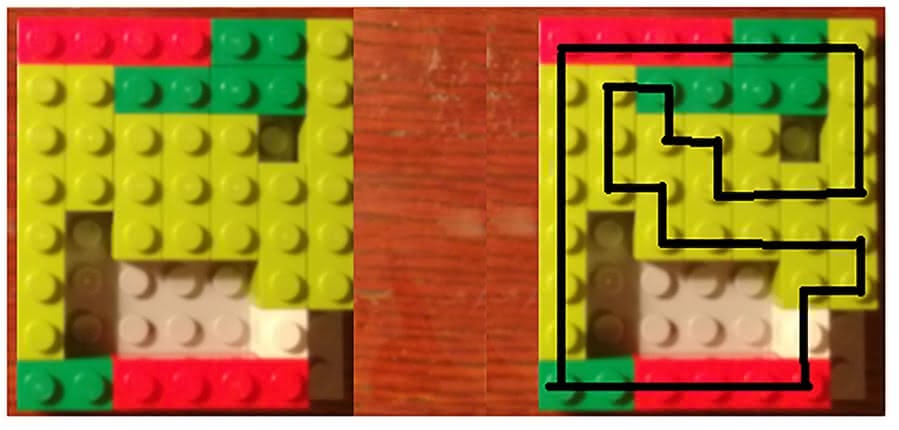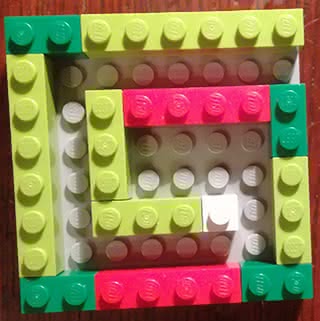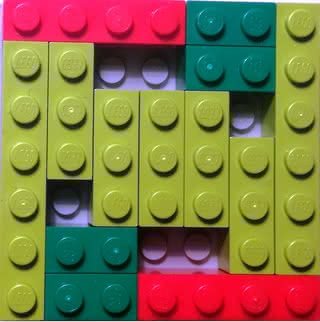Reforma, ach reforma
Obecna reforma organizacji szkolnictwa jest wyłącznie pomysłem politycznym, realizacją pewnej filozofii, wymyślonej w Prusach w XIX wieku, a zrealizowanej niedaleko od Polski w początku XX wieku: najpierw zburzymy to, co jest, a potem się zastanowimy. Owszem, merytorycznych argumentów za i przeciw jest dość dużo. Na własny użytek odkryłem, że od początków naszej niepodległości w XX wieku każda - bez wyjątku - nowa władza od razu zabierała się za reformę edukacji, zawsze obiecując, że nauczycielom będzie już lepiej. Odnotowałem, że obecny rząd jest pierwszy, który tego nie obiecuje. Dobre i to - przynajmniej tutaj jest szczery.
Szkoły powszechne ("ludowe") to wymysł Fryderyka Wielkiego. Nie z miłości dla ludu on to uczynił - doszedł do wniosku, że wykształcony żołnierz lepiej strzela.
Odnotujmy, że system takich szkół działał dość dobrze. Na ogół cokolwiek Niemcy robią, robią to dokładnie. Charakterystyczny jest przykład odkrycia talentu jednego z najwybitniejszych uczonych wszech czasów: Karola Fryderyka Gaussa (1777-1855). W wiejskiej szkółce koło Hanoweru inteligentny nauczyciel (!) zdał sobie sprawę, że niepozornie wyglądający chłopiec jest być może geniuszem. Przekazał więc chłopca "wyżej", sprawa doszła do księcia, który również potrafił docenić, kogo ma przed sobą, sypnął groszem na dalszą naukę… i świat zyskał kogoś naprawdę niezwykłego - a moja teza, że najważniejsi dla społeczeństwa są nauczyciele, zyskała jeszcze jednej przykład potwierdzający.
Sto lat edukacji
Ciekawy będzie króciutki przegląd systemów szkolnych panujących w Polsce w ciągu stu lat naszej nowej niepodległości.
Bardzo późno, bo dopiero w 1932 r., ustawa tzw. jędrzejewiczowska zaprowadziła porządek i scaliła różne systemy - pozostałości po zaborach. Do tego czasu funkcjonowały siedmioletnie szkoły podstawowe. Szkoły średnie miały system odrębny od podstawowych. Nauka w gimnazjum trwała osiem lat: trzy lata gimnazjum niższego i pięć gimnazjum wyższego. Teoretycznie uczeń po czwartej klasie szkoły podstawowej mógł kontynuować naukę w gimnazjum niższym, warunkiem było jednak zdanie egzaminu wstępnego, który często nie uwzględniał programu nauczania w szkole podstawowej. Dlatego tworzono przy gimnazjach tzw. klasy przedwstępne, mające przygotować do egzaminu. Istniały trzy typy gimnazjów: humanistyczne, matematyczno-przyrodnicze i klasyczne, z greką i łaciną. Gimnazjum wyższe kończyło się egzaminem maturalnym, który był podstawą przyjęcia na studia wyższe (bez egzaminu wstępnego). Szkolnictwo państwowe było płatne.
W 1932 r. przeprowadzono wspomnianą reformę edukacji, która połączyła system szkół podstawowych z ponadpodstawowymi. Szkoła podstawowa trwała wprawdzie wciąż siedem lat, jednak gdy uczeń chciał kształcić się dalej, zdawał do gimnazjum już po sześciu latach. Szkoła średnia dzieliła się odtąd na czteroletnie gimnazjum i dwuletnie liceum, po którym zdawano egzamin maturalny.
Po wojnie zostawiono siedmioletnią szkołę powszechną (w zmienionym nazewnictwie: podstawową), znikło gimnazjum, a liceum rozrosło się do czterech lat. Piszący te słowa zdawał maturę jako uczeń jedenastej klasy. Tak było do lat 70., kiedy to zaproponowano model radziecko-enerdowski dziesięcioletniej ogólnokształcącej szkoły średniej. Prasa zachłystywała się peanami na cześć tego pomysłu i jak to rośnie nam młody wykształcony Polak. "Każdy będzie miał średnie wykształcenie - oto dowód naszej troski o młode pokolenie!" Przypominało to sytuację afrykańskiego kacyka, który - aby rządzić narodem wykształconym - nadał wszystkim swoim poddanym stopień magistra. U niego było więc nawet lepiej niż w PRL - wszyscy mieli wykształcenie wyższe.
Muszę jednak oddać sprawiedliwość ówczesnym władzom edukacyjnym. Tamta reforma była jedyną, która została porządnie przygotowana. Istniały zatwierdzone programy (a nie nic nie znaczące "podstawy programowe"), przeszkoleni nauczyciele i administracja. I może właśnie dlatego reforma… nie weszła w życie. Ktoś rozsądny zorientował się, że to jeszcze nie ma sensu, a inni rozsądni działacze (wtedy wszyscy nazywani "komuchami") przyjęli racjonalne argumenty. Gospodyni domowa, która by się uparła, że zamiast cukru do pieczenia ciasta trzeba wziąć soli, nie może przecież liczyć na to, że goście będą chwalić wypiek - niech lepiej wyrzuci wszystko przed podaniem.
Skończyło się więc na najdłużej trwającym systemie 8 + 4. Programowi matematyki należy się osobny akapit, ale na razie mówię tylko o organizacji. Pod koniec lat 90. wrócono do pomysłu przedwojennego trójstopniowego systemu, tym razem w wersji 6 + 3 + 3 i - nie dyskutując z realiami - reformę wdrożono. Upłynęło jednak kilkanaście lat, powstały w tym czasie dobre gimnazja, a co najważniejsze, nauczyciele nauczyli się pracować w tym systemie. W światowych badaniach edukacyjnych podskoczyliśmy o kilkanaście miejsc, lądując w czołówce Europy.
Odnotuję jeszcze, że o ile w szkolnictwie wyższym dążymy obecnie w Europie do przyjęcia jednolitego systemu (tzw. system boloński) i mimo oporów oraz nonsensów z tym związanych "jakoś to idzie", to w edukacji dzieci "każdy sobie rzepkę skrobie". Ile krajów, tyle systemów. I bardzo dobrze. W edukacji jest bowiem jedna zasada, a mianowicie: nie ma żadnych zasad.
* * *
Świat wokół nas zmienia się w oszałamiającym tempie. Największym wynalazkiem naszych czasów okazać się może Internet, przewidziany proroczo przez Stanisława Lema (w jego niesamowitej książce z 1959 r. "Powrót z gwiazd" - sam Lem dziwił się, jaki wpływ miała ta niezbyt literacko udana książka na całe pokolenie). Szkoła nie może pozostać obojętna na zmiany. Powinniśmy zastanawiać się nie tylko, jak uczyć, ale - w XXI wieku przede wszystkim - czego uczyć. Mamy przecież przygotować nasze dzieci do zawodów, które jeszcze nie istnieją! Może nie ma nawet nazw tych profesji. Pamiętajmy, że to my, nauczyciele (wszystkich szczebli) mamy największy udział w tzw. PKB. My naprawdę jesteśmy najważniejsi!!! Oświata to oś świata!!! Od nas zależy, jakie będą nasze Rzeczypospolite… , no właśnie, nie od razu, ale za 20-30 lat. Nie pracujemy ani dla siebie, ani dla naszych dzieci. Dla wnuków. Czy to dla Państwa zbyt odległa perspektywa? Róbmy swoje!
Niewiele dobrego da się powiedzieć o systemie kształcenia nauczycieli. Nonsensy zaczęły się wtedy, kiedy wszystkich pedagogów (to znaczy tych już czynnych, pracujących w zawodzie) zapędzono na studia wyższe - i to w dodatku "bez odrywania od pracy". Szkoły wyższe nie zmieniły programów nauczania, bo "dyplom jest jeden!" Skutek: nauczyciel po męczącej pracy w szkole szedł na wykłady i ćwiczenia. Ja byłem dobrym studentem, ale mogłem zajmować się studiami po kilkanaście godzin dziennie. Nie potrafiłem sobie wyobrazić, jak jest temu w stanie podołać ktoś, kto "normalnie" pracuje. Szkoda pisać dalej…
Potem było różnie. Tym niemniej brak porządnie wykształconych nauczycieli jest przyczyną zapaści polskiej edukacji. Diabeł tkwi w szczegółach. Co znaczy "porządnie wykształcony"? A, to temat na inne opracowanie. Na pewno jest to tylko luźno związane ze stopniami i tytułami naukowymi.
Poszukujmy nieustannie nowych metod i nowych treści nauczania. "Poszukujmy" nie równa się jednak „od razu wdrażajmy - wyrzucamy stare, przyjmujemy nowe”. Nie. Wdrażajmy tylko to, co lepsze. Nierzadko nowe oznacza jedynie blichtr, fasadę albo odgrzanie starych kotletów. Rzeczywiście, może nie ma sensu uczyć dzieci, jak rozpalać ognisko bez zapałek - ale już orientowanie się w stronach świata według Słońca ma sens, nawet jeśli każdy dysponuje GPS-em. Zachowajmy zdrowy rozsądek nawet w XXI wieku.
Klocki do wyczarowywania matematyki
Jednym z ciekawszych pomysłów dydaktycznych jest upowszechnienie klocków Lego, o czym wspominaliśmy już przed miesiącem. Tym razem omówię modelowe zajęcia dla nauczycieli, prowadzone przez firmę LEGO Education, wg własnych scenariuszy. Na tym przykładzie wypowiem się, czego bym oczekiwał od nauczycieli nauczania początkowego.
Na pewno nie tego, co widziałem już kilka razy. Pani nauczycielka oświadcza oto, że zadanie o równoległoboku jest dla niej za trudne. Inna boi się słowa "prostopadłościan". Ktoś tam nawet nie otwiera mojej książki, popularnej, "bo tam jest sama matematyka". Pewna pani "nie znosi geometrii", ktoś dzieli przez zero, ktoś inny nie umie dostrzec nic charakterystycznego w ciągu liczbowym 1, 3, 5, 7, 9, 11, 13, … i tak dalej. Dziwię się, że moi studenci nie potrafią ujrzeć związku między ciągiem liczb Fibonacciego: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …. a ciągiem 5, 9, 14, 22, 35, 56, 90, 145, 234, ….. Teraz wiem, skąd się bierze ten brak spostrzegawczości liczbowej. I tego przede wszystkim uczę studentów informatyki.
Zestaw edukacyjny klocków Lego dla klasy pierwszej szkoły podstawowej składa się z szarej podkładki i klocków jak na fot. 1. Jeden z klocków ma rozmiar 1x1 i narysowane oczko. Będzie ono oczkiem węża w proponowanym ćwiczeniach.
Spojrzałem na ten zestaw z punktu widzenia "zawodowego matematyka". Spodobał mi się, zacząłem sam się nim bawić. Okazało się, że potrafię "wyczarować" z niego spory kawałek "prawdziwej" matematyki. Moi koledzy zarzucą mi wymyślenie terminu prawdziwa matematyka. Jeżeli bowiem jest prawdziwa, to pewnie jest i nieprawdziwa. Być może, ale nie wejdę w tę dyskusję.
Powiem tak. Spodobał mi się w tym zestawie układ liczb guziczków w poszczególnych klockach - odłożę jednak tę kwestię do następnego artykułu. Z punktu widzenia matematyki "uniwersyteckiej" bardzo ciekawe jest natomiast zadanie, które wchodzi w geometrię algebraiczną, tzw. teorię podziałów, algebrę tensorową i działy matematyki nieznane studentom z wykształceniem politechnicznym (oraz żadnym innym poza wąską i trudną gałęzią - właśnie algebrą tensorową). Nie wiem, czy układający to zadanie (ma numer 5) zdawali sobie z tego sprawę. Chyba nie.
Na zajęciach z nauczycielami powiedziałem właśnie coś takiego: jestem jedynym na sali, który widzi głębię tego zadania - nie dlatego, że jestem "taki mądry", tylko po prostu dwadzieścia lat zajmowałem się tym profesjonalnie. Byłoby absurdem oczekiwać, że taką samą wiedzę powinni mieć nauczyciele. Ale zachęcam do dyskusji na inne tematy, które niżej poruszam: symetrii, klasyfikacji, ciekawostek liczbowych - chciałbym, żeby nauczyciele to właśnie umieli przekazać uczniom, choćby w formie zachęcenia ich do wycieczki w tamtą stronę (proszę też przeczytać niżej o tym, dokąd pójść ze szczytu Grzesia w Tatrach Zachodnich). Jeśli coś jest piękne w zawodzie nauczycielskim, to właśnie umiejętność skierowania ucznia we właściwą stronę: idź tam, zobaczysz coś ciekawego, zainteresuj się, może to Twoja życiowa droga?
No dobrze, koniec dygresji. Nie, nie koniec! "Muszę" jeszcze jedno. W latach 70. poprzedniego stulecia próbowano nauczycieli i uczniów uczyć, serwując im - od przedszkola począwszy - streszczenie uniwersyteckiego kursu matematyki. No i jak to się miało skończyć?!
Wracajmy do naszych zadań i do Lego. Na białym klocku jest namalowane oczko - będzie to oczko węża, którego zaraz ułożymy (tzn. ułożą go dzieci). Najpierw długości 6, to łatwe. Potem długości 10 (tu trzeba węża załamać). Potem następuje kontrowersyjne, ale bardzo ciekawe zadanie: ułóż najdłuższego węża.
Dlaczego kontrowersyjne? Sugerowaną odpowiedzią jest 44, czyli trzeba uwzględnić wszystkie klocki i zwinąć węża w kłębuszek. Owszem, wąż tak może się zwinąć. Ale i ja, i około połowa moich "respondentów" uważamy, że wąż nie powinien stykać się sam ze sobą. Dlaczego mogę mieć rację? Wąż to linia, a w każdym razie coś podłużnego, a czy kwadrat jest podłużny? Druga wątpliwość: jeżeli wąż wygląda tak, jak na fot. 2a, to gdzie ma ogon? W którą stronę ogon idzie za głowę? Oczywiście to mogą być pytania bez znaczenia, zwłaszcza, że rzecz dzieje się na żywo i można wątpliwości natychmiast wyjaśniać…
Zadanie 1. (trudne, a na pewno trudne dla pierwszaków). Czy to, co widzimy na fot. 2a, jest wężem? Co to znaczy, że "jest wężem"? To znaczy, że można tę figurę uczynić linią łamaną. Spróbujmy (fot. 2b). Napisałem przed chwilą, że "mogę mieć rację". Nie muszę, zdaję sobie sprawę z tego, że nie muszę. Nie chcę się tu wdawać w dyskusję, która może zainteresowałaby zawodowych dydaktyków. Ale zadałem sobie pytanie, czy efekt jest ładny? Czy wzorek mi się podoba? I oczywiście zacząłem układać inne. Nie można wymierzyć, która układanka będzie ładniejsza od innej. Ale można zadać pytanie: który wąż jest najładniejszy. Głosujmy.
Zadanie 2. Ułóż możliwie najładniejszego węża. Wykorzystaj prawie wszystkie klocki. Ale czemu ograniczać się do węży?
Zadanie 3. Stwórz możliwie najładniejszą układankę, wykorzystując wszystkie klocki (łącznie z oczkiem węża - albo bez niego). Mnie podobają się takie (fot. 4, 5). Mają one symetrie - pierwsza osiową, druga - środkową.
Zadanie 4. Ułóż ornament symetryczny, który nie miałby "dziur" takich, jak mój na fot. 6.
Czy potrafisz ułożyć ornament, który by miał symetrię osiową, ale względem osi x, tzn. poziomej? A pionowej? Ta układanka ma też symetrię środkową Następne zadanie w zestawie LEGO Education dla pierwszoklasisty jest bardzo ciekawe… i mało kto sobie z tego zdaje sprawę. Jest w Tatrach Zachodnich niezbyt ambitny szczyt Grześ, w sezonie pełen turystów na zabierających pół dnia wycieczkach z Doliny Chochołowskiej. Wystarczy skręcić z niego na zachód, na stronę Osobistej, by po kilkunastu minutach znaleźć się w innym świecie. Ale nie rozmarzajmy się. Zadanie "firmowe" brzmi następująco:
Zadanie 5. Zbuduj węża o długości 14, używając do tego sześciu klocków.
Zadanie można rozwiązać na wiele sposobów. Wąż musi mieć głowę. Zostaje zatem pięć klocków na ułożenie ogona o długości 13. Jakie wziąć klocki z naszego zestawu? Są tylko dwie możliwości: 13 = 4 + 3 + 2 + 2 + 2 = 3 + 3 + 3 + 2 + 2. Zatem istnieją tylko dwie możliwości na ułożenie węża!
Oj, czy naprawdę tylko dwie? To mamy tylko dwa węże? Zależy od punktu widzenia. Czy węże na fot. 7 mamy uważać za inne, czy takie same? Można powiedzieć, że to ten sam wąż, tylko inaczej zwinięty. Tak mówisz? To proszę, zadanie: Zadanie 6. Na ile sposobów może się ułożyć wąż widoczny na fot. 7?
Zadanie 7. Ułóż… następne zadania. Nie, to nie pomyłka. Sam ułóż. Dam kilka podpowiedzi.
Zadanie 8. Puszczając wodze fantazji, wyobraź sobie, że węże z gatunku jak na fot. 7 to samce. Samiec odznacza się tym, że ma ogon w kolorach takich, jak tam: czerwonym, jasnozielonym i ciemnozielonym. Kolejność kolorów jest dowolna, ale nie może być "łat", tzn. układ jasnozielony-ciemnozielony-jasnozielony nie jest dopuszczalny. Ile typów samców jest możliwych?
Zadanie 9. A gdy dopuścimy "łaty"?
Zadanie 10. No, to uznajmy za samiczki węże typu 3 + 3 + 3 + 2 + 2. Ułóż takiego węża. Na ile sposobów może się zwinąć w łamaną? Ile jest typów samiczek?
Zadanie 11. Powtórz poprzednie zadania dla wężów innej długości.
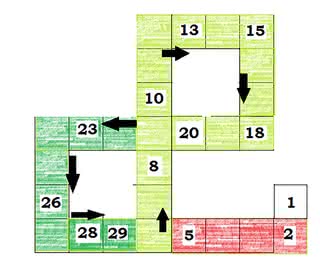
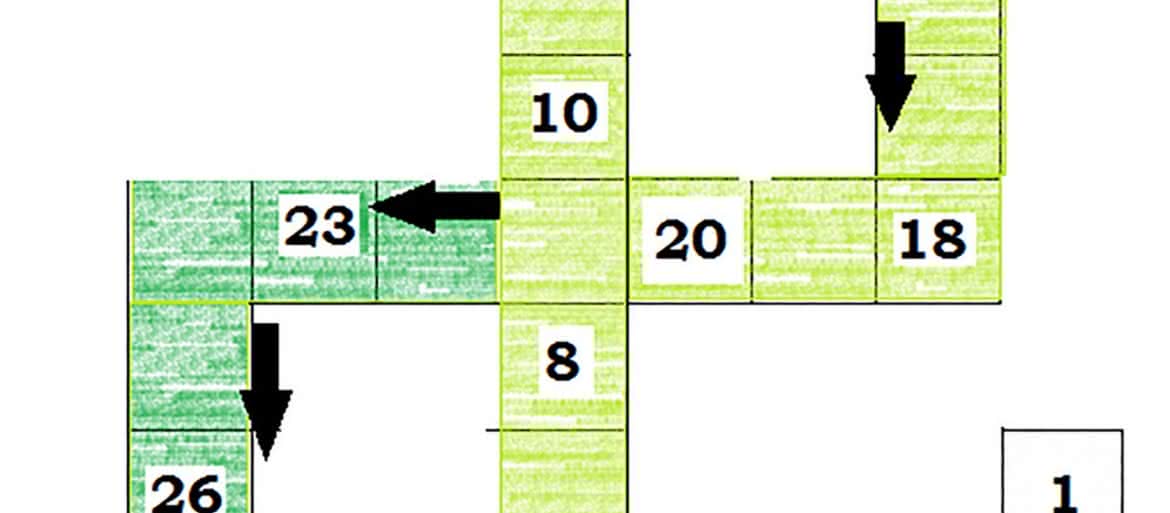
Zadanie 12. Zaskocz nauczyciela pytaniem: jaką długość ma wąż ułożony na rys. 1. Zwinął tylną część ciała w ósemkę i śpi zadowolony. Jeżeli nauczyciel stwierdzi: "na tułów (ogon) zużyłeś pięć klocków trójguziczkowych, cztery dwuguziczkowe, jeden czteroguziczkowy, a wliczając głowę - 28, a więc wąż ma długość 28" - wówczas odpowiedz: "to liczmy tak, jak przy grze w Chińczyka. Ile kroków jest potrzebnych na przejście pętli (rys. 1)? Startuję z głowy i po 29 krokach jestem na polu, z którego do zamknięcia pętli mam jeszcze krok. To znaczy, że długość jest równa 30. Rys. 1. Wąż "liczony" klockami lub krokami
Zadanie 13. Na fot. 8 nie zwracaj uwagi na kolory. Ile guziczków widzisz w kolejnych warstwach? Jak się nazywają takie liczby? Dodaj je wszystkie. Otrzymałeś 36, a to jest sześć razy sześć. Ułóż kwadrat 6 na 6.
Zadanie 14. A co ciekawego widzisz na fot. 9?