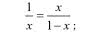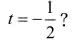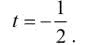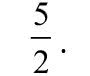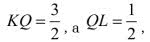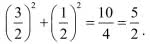Kwadrat
Nastolatku: musisz już wiedzieć, co mówi znak drogowy z rysunku 1.
Ćwiczenie. Jakie sporty uprawia się na kwadratowym polu? Podam jeden przykład: ring bokserski. Poszukaj innych.
Teraz swego rodzaju zestaw obowiązkowy z matematyki. Kwadrat o boku a ma obwód 4a i pole a2. Właśnie dlatego druga potęga liczby (a więc jej iloczyn przez siebie samą) jest nazywana kwadratem. Przekątna kwadratu jest równa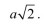 
W mojej szkole (to znaczy tej, w której byłem uczniem) należało pamiętać, że w przybliżeniu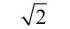 
to 1,4142 - trochę mniej niż półtora.
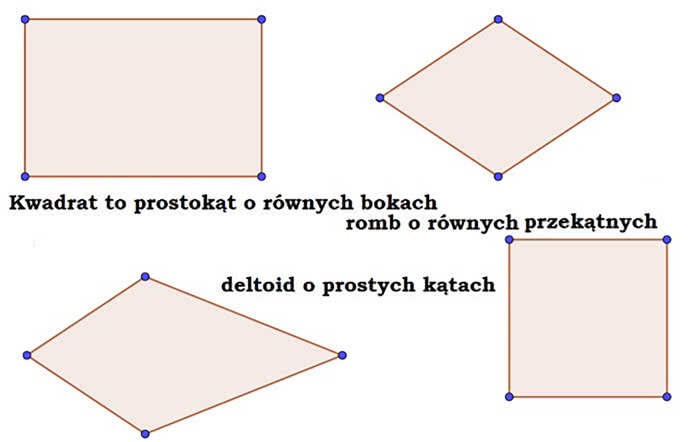
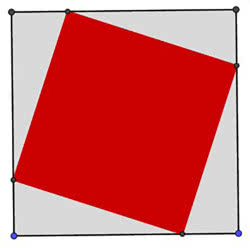
Matematycznie rzecz biorąc, kwadrat jest prostokątem. Pewnym specjalnym, ale jednak prostokątem. Jest też rombem i deltoidem. Przypomnę, że deltoid wygląda jak latawiec (rysunek 2). W języku potocznym jest nieco inaczej: nawet matematyk powie: "mój pokój nie jest kwadratowy, ale prostokątny". Odróżniajmy jednak dopuszczalne kolokwializmy od precyzyjnego języka matematyki. Na przykład, podoba mi się celne określenie sprawozdawców piłkarskich: bramkarz skrócił kąt. Matematycznie jest bezsensowne: kąt nie ma długości. Ale wiadomo, o co chodzi.
Tak sformułowane określenie kwadratu (jak w podpisie do rysunku 2) spełnia arystotelesowskie wymagania co do definicji pojęć: genus proximum et differentia specifica. Na polski tłumaczymy to jako "najbliższy rodzaj i różnica gatunkowa". Można i należy to rozumieć tak:
- Rodzaj: prostokąty. Różnica gatunkowa: równe boki.
- Rodzaj: romby. Różnica gatunkowa: równe przekątne.
- Rodzaj: deltoidy: Różnica gatunkowa: kąty proste.
Zadanie (trochę z matematyki, a trochę na rozumienie, o co chodziło Arystotelesowi). Wykaż, że w rodzaju "wielokąty" kwadrat jest wyróżniony przez różnicę gatunkową: 16 pole = obwód2. Najpierw: wyraź to prościej, o co w tym chodzi.
A oto następne zadanie, między życiem a matematyką. Z doświadczenia wiemy, że pokój "kwadratowy" jest mniej ustawny niż prostokątny (oczywiście użyłem tu obu określeń w potocznym sensie) - byle prostokąt nie był zbyt "podługowaty". Czy jest w tym jakaś matematyka?
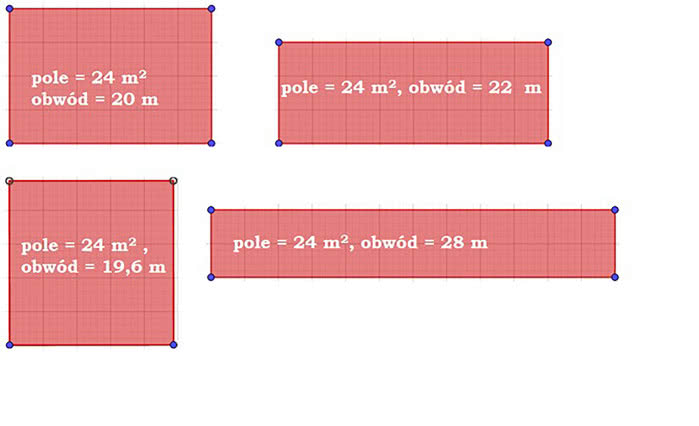
Oczywiście, że jest (jak we wszystkim). Przypatrzmy się różnym pokojom o 24 metrach kwadratowych.
Widzimy, że im bardziej wydłużony prostokąt, tym większy ma obwód. Meble w pokoju stawiamy raczej przy ścianach. Dlatego im większy obwód, tym więcej możemy ustawić… dopóki długość nie stanie się zbyt uciążliwa. Przypomnę i zasadę złotego podziału. Można ją sformułować tak: całość ma się do większej części tak, jak większa do mniejszej. Jak się to wyraża matematycznie? Jeżeli całość oznaczymy przez 1, a większą część przez x, to mamy równanie
po jego rozwiązaniu dostajemy przybliżenie x=0,618. Prostokąt, którego boki pozostają w złotym stosunku, wygląda tak, jak na rysunku 4. Dodajmy, że flaga Polski ma być prostokątem o rozmiarach 8:5, co jest bliskie złotemu podziałowi. Ale pokój mieszkalny o tym kształcie było jednak zbyt "podługowaty".
Zadanie. Wykaż, że spośród prostokątów o tym samym obwodzie, kwadrat ma największe pole.
Nauczyciele akademiccy mają tendencję do dowodzenia takich faktów za pomocą rachunku różniczkowego. Owszem, jeżeli bokami prostokąta są x, y, obwodem 2p, to y=p–x, a polem jest xy=x(a–x). Pozostaje znaleźć wartość największą widocznej funkcji kwadratowej.
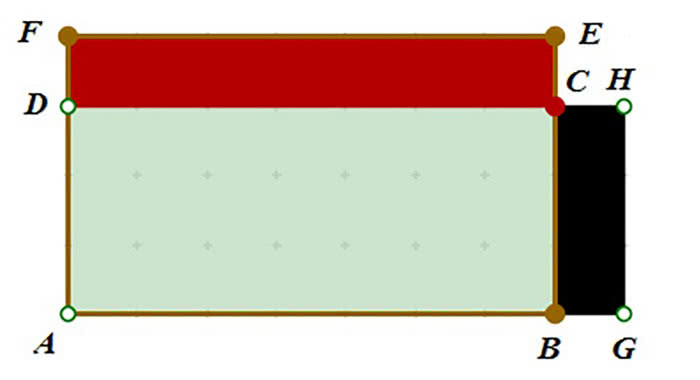
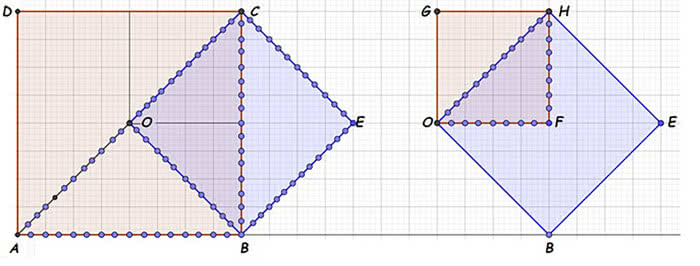
Ale nas interesują metody geometryczne. Spójrzmy na rysunek 5. Jeżeli prostokąt AGHD nie jest kwadratem, to ma nierówne boki. Można wtedy skrócić jeden bok, a przedłużyć drugi, żeby otrzymać prostokąt o trochę większym polu. Pole CEFD jest większe od pola BGHC. A zatem tylko kwadrat może mieć największe pole w klasie wszystkich prostokątów o tym samym obwodzie. Czy to znaczy, że kwadrat ma największe pole w klasie wszystkich prostokątów o tym samym obwodzie? Dziwne pytanie. No, przecież właśnie to wykazaliśmy.
Jeszcze nie. Spójrzmy na takie rozumowanie, mające "wykazać", że liczba 2021 jest największa. Dla każdej liczby mniejszej od 2021 da się znaleźć większą od niej, a więc istotnie 2021 jest największa. Gdzie robimy błąd?
Mianowicie tu, że zakładamy, że w ogóle istnieje liczba największa. Założenie jest jednak błędne, wobec tego oparte na nim rozumowanie jest nic niewarte i nic nie daje. Mamy jeszcze zatem przekonać się, że wśród wszystkich prostokątów o tym samym obwodzie istnieje jeden o największym polu. Zwracam uwagę, że takiego prostokąta o najmniejszym polu nie ma! I to posłuży mi do dowodu, że największe pole jest osiągalne. Jeżeli prostokąt o stałym obwodzie jest bardzo długi i wąski, to pole jest bliskie zera. Podobnie, gdy jest bardzo wysoki o niewielkiej podstawie. Między tymi skrajnościami musi gdzieś być maksimum.
Przypominałem już, że przekątna kwadratu jest liczbą niewymierną
Obecnie niewymierność tej liczby wykazujemy prostym rozumowaniem algebraicznym. Uczniowie słabo rozumieją, o co w tym wszystkim chodzi. Komputery… też nie. Liczby niewymierne nie są w ogóle potrzebne do obliczeń praktycznych. Co mi z informacji, że do pomalowania okrągłego boiska potrzeba, powiedzmy, kilograma farby. W takich opakowaniach farby się nie sprzedaje. W sklepie muszę to i tak przeliczyć na "zwykłe" liczby.
A jednak liczby niewymierne odegrały niesłychanie ważną rolę w historii cywilizacji europejskiej. Europejską filozofię poznawania świata zawdzięczamy Pitagorasowi. Jego szkoła-sekta pierwsza zaczęła przyglądać się światu oczami rozumu. Dla pitagorejczyków wszystko było liczbami i stosunkami liczb - oczywiście tylko liczb takich, jak 1, 2, 3, 4,…, 100,… Dzisiaj nazywamy je liczbami naturalnymi. I nagle odkryli, że przekątna kwadratu taką liczbą nie jest… to znaczy długość tej przekątnej. To piękne rozumowanie.
Dokładniej, pitagorejczycy odkryli, że przekątna kwadratu nie jest współmierna z jego bokiem. Nie ma takiego odcinka, który mieściłby się całkowitą liczbę razy i w przekątnej, i w boku. Jak udowodnić, że czegoś nie ma? Służą do tego dowody nie wprost. Stosujemy je bezwiednie i na co dzień.
Przypuśćmy, że bok kwadratu ABCD jest współmierny z przekątną. Na rysunku 6 małe odcineczki wypełniają i bok, i przekątną. Długość takiego odcinka s nazwiemy wspólną miarą boku AB i przekątnej AC. Co widzimy? Że to samo s jest wspólną miarą mniejszego kwadratu BECO i jego przekątnej BC. Ważne, że to to samo s. Skoro jednak tak, to owo s będzie wspólną miarą dla jeszcze mniejszego kwadratu i jego przekątnej. Skoro tak, to owo s będzie wspólną miarą dla jeszcze mniejszego kwadratu i jego przekątnej. Celowo powtórzyłem poprzednie zdanie. Kwadraty będą się zmniejszać i zmniejszać, a wspólna miara nie będzie się zmieniać. Wreszcie kwadraty staną się rozmiarów mniejszych niż s… Tak być nie może. Coś jest źle! Co?
Po prostu nasze przypuszczenie, że owa wspólna miara w ogóle istnieje, było błędne. Nie ma jej! Co za rozumowanie! Ponad 2500 lat temu! Może dlatego dzisiaj matematyka jest taka trudna, skoro już była taka ćwierć dekady temu (licząc za dekadę dziesięć tysięcy lat)?
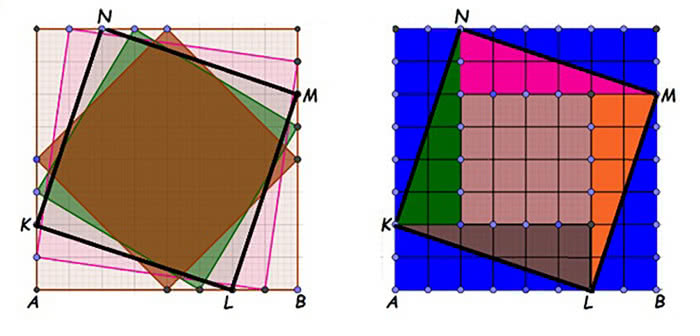
Bardzo lubię zadania z geometrii typu "dorysuj jedną kreskę, a rozwiążesz". Czy umiesz wyznaczyć pole mniejszego, czerwonego kwadratu na rysunku 7? Oczywiście w stosunku do pola całego kwadratu? Nie? To spójrz na rysunek 8 (szczególnie ten po prawej stronie). Już wszystko jasne? Na pewno. Trzeba było dorysować więcej kresek niż jedną, ale na dobrą sprawę to umieścić wszystko na kratkowanym papierze.
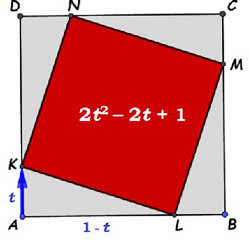
Podejdźmy do tego zadania inaczej. Niech kwadrat ABCD ma boki długości 1. Wyobraźmy sobie, że punkt K porusza się jednostajnie do góry, w czasie od 0 do 1, ciągnąc za sobą cały kwadrat KLMN. Kwadrat ten zmniejsza się i obraca, gdy czas t dojdzie do 1, obróci się o całe 90 stopni. Ale nie to nas interesuje, tylko jego pole. Spójrzmy na rysunek 9. Z twierdzenia Pitagorasa obliczymy, co trzeba, to znaczy bok KL. Jest ona przeciwprostokątną w trójkącie KAL. Mamy oto wzór na pole zmiennego kwadratu. Sprawdźmy. Co się dzieje w połowie między 0 a 1, czyli w punkcie czasowym
Kwadrat zmienił się na mniejszy, położony tak, jak znak drogowy na rysunku 1. Pole takiego kwadratu to połowa pola ABCD.
I teraz, gdy wędrujący po AD punkt przystanął na chwilę w połowie swej drogi, jest miejsce na wielopiętrową dygresję. Kwadrat wpisany ułożył się tak, jak… u Sokratesa. Otóż w tekście Menon (bo trudno to nazwać książką) Platon opisuje, jak Sokrates nauczał chłopca geometrii. Polecił chłopcu narysować na piasku kwadrat, a potem narysować kwadrat dwa razy większy. Chłopiec narysował oczywiście tak, jak na rysunku 10. Wypada ze smutkiem stwierdzić, że 2400 lat po Sokratesie błąd ten powielają niektórzy nauczyciele, tłumacząc uczniom, że to, co narysowane w skali 1:2, jest dwa razy mniejsze. Polecam taką analogię: bierzemy mapę Polski w skali jeden do miliona. Jest to arkusz zbliżony rozmiarem do rozłożonej gazety. Polska ma 38 milionów mieszkańców, a zatem na takiej mapie miałoby się zmieścić 38 ludzi! Gdzie jest błąd w rozumowaniu?
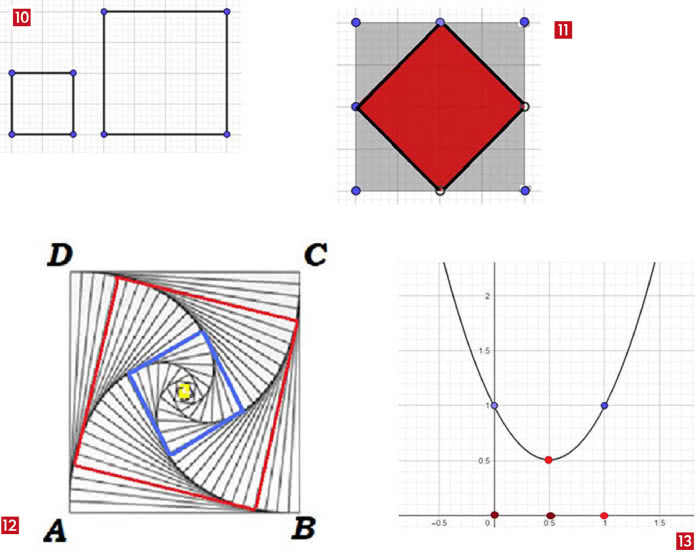
Metodą inteligentnie stawianych pytań Sokrates spowodował, że chłopiec sam doszedł do prawidłowej odpowiedzi, oczywiście tej, jak na rysunku 11. Stworzył w ten sposób metodę nauczania, zwaną dzisiaj właśnie sokratejską, a filozofom greckim zdarzenie to stało się przykładem, że wszyscy mamy w sobie jakąś przyrodzoną wiedzę, a rolą nauczyciela jest pomóc tej myśli wydobyć się na świat (matka Sokratesa była, używając dzisiejszej terminologii, akuszerką). Teoria ta odżywała w różnych formach i postaciach przez tysiąclecia. Autor tych słów uważa, że cała dydaktyka ogólna to tylko przyczynki do Sokratesa. Ale nie afiszuję się z tym poglądem.
Dygresja miała być wielopiętrowa. Azor, Burek, Czaruś i Drops stoją sobie spokojnie w wierzchołkach kwadratu ABCD (rysunek 12). Nagle Azor poczuł "coś" do Burka, Buruś do Czarka, Czarek do Dropsa, a Drops do Azora. Każdy pobiegł w kierunku tego drugiego… i co się stało? Pieski zatoczyły łuki i znajdując się zawsze w wierzchołkach obracającego się i malejącego kwadratu, spotkały się w samym środku. Fizycy nazwaliby ten punkt punktem osobliwym - co tam się działo, nie da się opisać równaniami. W końcu państwo Andrzej, Basia, Celina i Damian odciągnęli swoich pupilów i nawet z żadnym z nich nie trzeba było jechać do weterynarza. A krzywa, po której biegły, nosi w literaturze matematycznej taką właśnie nazwę: psia krzywa. Jej długość wyraża się skomplikowaną całką. Dobrze, że pieski o tym nie wiedzą.
Będzie jeszcze następne piętro dygresji. Widzieliśmy, że pole kwadratu, obracającego się tak, jak na rysunku 8, jest równe 2t2-2t+1. Niech czas t biegnie od zera do jedynki. Przypomnijmy sobie z liceum parabolę, wykreślmy funkcję y=2t2-2t+1. Zgadza się: w położeniu zerowym "mały" kwadrat pokrywa się z dużym, potem maleje do tego "sokratejskiego" i w takim samym tempie rośnie. Jak częściowe zaćmienie Słońca przez Księżyc. Takie zaćmienie nazywane jest w astronomii obrączkowym.
Pokolenia matematyków i fizyków dziwiły się, że w równaniach jest jakaś zaklęta mądrość, że jest w nich więcej, niż włożyliśmy w nie. Zobaczmy i my. Co się działo, gdy… jeszcze się nic nie działo, gdy nas nie było na świecie? W naszym przykładzie: co było w czasie ujemnym, na przykład dla
Wartością funkcji jest
Tyle jest równe pole "małego" kwadratu KLMN. Jak to? Dwa i pół? Przecież cały kwadrat ABCD ma pole 1 ?
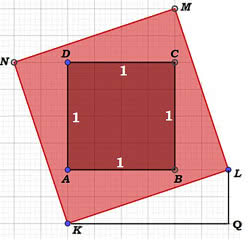
Rysunek 14 wyjaśnia tę pozorną sprzeczność. Dla ujemnego czasu kwadrat KLMN jest położony tak, jak na tym rysunku. Obliczmy jego pole inaczej, standardowo. Stosujemy twierdzenie Pitagorasa do trójkąta KQL. Odcinek KQ ma długość sześciu "kratek", ale za jednostkę bierzemy cztery, zatem
więc kwadrat przeciwprostokątnej KL to właśnie
Naprawdę, równanie myśli za nas. Trzeba tylko umieć z nim się porozumieć. Nieco podobnie jest z komputerem. Obliczy, co mu zlecimy, ale to my osobiście musimy zrozumieć, co owo żelastwo nam wyrzuciło na ekran.
I już ostatnie piętro dygresji. Na pewnym wykładzie użyłem właśnie tego określenia: "żelastwo". Obecny na sali wybitny informatyk, profesor wiodącej uczelni, pouczył mnie: "panie kolego, w komputerze nie ma ani atomu żelaza!". Rzecz jasna, podziękowałem za tę informację, a profesor poczuł się dowartościowany.
Na zakończenie taki oto quiz; dałem go stypendystom Krajowego Funduszu na rzecz Dzieci, na warsztatach matematycznych.
- Co to jest kwadratura koła? Czy może to to samo, co zawracanie Wisły kijem, czy jednak ma to inny odcień znaczeniowy?
- Ile minut trwa kwadrans? Gdy zbliżała się szósta, twój prapradziadek mógł powiedzieć, że jest „trzy na szóstą”. Która to była godzina? Co to ma wspólnego z liczbą cztery?
- W jakim sporcie mecz dzieli się na kwarty? W przewodniku po Tatrach z XIX wieku jest wspomniane, że kwarta masła kosztowała 50 centów. A pół wieku temu ja na wycieczce na Babią Górę nazbierałem sobie pełną kwaterkę malin. To ile tego było? A może potrafisz zagrać na fortepianie kwartę? W tym samym przewodniku jest informacja, że fotografia in quarto kosztuje 80 centów. Jakiej wielkości była ta fotografia?
- Gdy Księżyc jest w pierwszej kwadrze, to czy bliżej mu do nowiu, czy do pełni?
- Kiedy była w użyciu kwadryga? A może wiesz, jaką figurą geometryczną jest kwadryka? Powiem tylko, że sfera, czyli powierzchnia kuli, nią jest. Jak myślisz, jaki stopień dostaniesz, gdy powiesz na lekcji matematyki, że skoro wykresem funkcji liniowej jest linia, to funkcji kwadratowej - kwadrat?
- Jeśli zostaniesz lekarzem, to będziesz się uczyć o kwadricepsach i kwadriplegikach. To znaczy o czym i o kim?
- Generał przyjechał na inspekcję do wojsk ONZ, pilnujących rozejmu w pewnym mieście. Koszary były puste. Pułkownik tłumaczył: "W poprzednim kwartale kwaterowaliśmy w innym kwartale" - co to znaczy?
- Czy odezwałeś się kiedyś do kogoś: "ty ośle kwadratowy"? Jeśli tak, to trochę nieładnie, nawet jeżeli ten ktoś na to zasłużył.
Michał Szurek
Zobacz także:
Dzielimy na pół - trójkąty i kwadraty
Kolorowe kwadraty i zaćmienia Słońca
