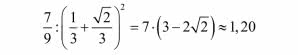Kwadratowe kwadraty
Terminologia matematyczna płata nam niekiedy figle. Wystarczy uświadomić sobie, że znane pojęcie "trójkąta prostokątnego" jest co najmniej dziwne, bo przecież trójkąt prostokątem być nie może. Ale do tego przywykliśmy. W matematyce uniwersyteckiej mamy pojęcie zbioru domkniętego i zbioru otwartego. Okazuje się, że jeżeli zbiór nie jest otwarty, to nie musi być wcale domknięty, a jest jeszcze gorzej, bo może być jednocześnie otwarty i domknięty. Każdy chyba nauczyciel miał ucznia, który na pytanie, co jest wykresem funkcji kwadratowej, odpowiedział "kwadrat" i uzasadnił: "bo wykresem funkcji liniowej jest linia". Takie rzeczy są obecne i w języku prawniczym - po prostu w żargonach zawodowych słowa mają niekiedy trochę inne znaczenie niż potoczne.
No, ale z tym, że kwadrat jest kwadratowy, zgodzi się każdy. Kwadrat stanowi szczególny przypadek prostokąta, chociaż w języku codziennym niekiedy przeciwstawiamy kształt kwadratowy prostokątnemu. Prostokąt o rozmiarach 11×12 jest "prawie" kwadratowy, a ten o bokach 10 i 20 staje się już bardzo odległy od kwadratu. Również kiedy zobaczymy pokój w kształcie trapezu o wymiarach 5×5×5×4 m, powiemy, że mamy prawie kwadratowy salon. A czy można powiedzieć, jak bardzo figura jest podobna do kwadratu? Na ile procent?
Matematyka to język liczb, kształtu i miary. Będziemy mierzyć stopień podobieństwa figur do kwadratu. Przedstawię to w formie dostępnej dla uczniów szkół podstawowych.
Pomiar ludności na Wyspie Prostokątnej
Na Morzu Figurowym (jest to właściwie zatoka Oceanu Niewielkiego) leży Wyspa Prostokątna - zamieszkała przez figury, których wszystkie kąty są proste. Mieszkańcy są różnych kolorów, każdy ma swój specyficzny kolor. Rasizm nie istnieje.
Starożytne legendy na wyspie mówią o innych istotach, nawet całkowicie okrągłych, ale wyobrazić ich sobie nikt nie umie. Od wielu pokoleń rządzi tu dynastia Kwadratowa. Oto portrety członków dynastii (1), od Kwadratu Maleńkiego, poprzez coraz większe, aż po Kwadrat X Niebieski. Znak X to nie iks, tylko rzymska cyfra oznaczająca Dziesięć. Czy znasz rzymskie cyfry, a właściwie znaki do zapisywania liczb? Pomówimy o tym kiedy indziej. Na razie mamy inne zmartwienie. Następca tronu, książę Żółty, nie jest już kwadratowy. Jakie ma rozmiary? Ano 11×12. Co zrobić z dynastią? Może wpuścić do niej trochę świeżej krwi?
O właśnie, w związku z tym zarządził król przegląd poddanych swoich. Kto najbardziej go kocha, króla swego, kto najbardziej jest do niego podobny? Najpierw uczeni-matematycy formułę stosowną opracowali. Z należytym szacunkiem pomierzyli króla i wszystkich Kwadratowych. Następnie przyjęli, że ci będą mieli Jedynkę - nie taki stopień szkolny, tylko Pierwszą Kategorię Obywatela. I rozjechali się mierniczowie po całej wyspie, miarkę każdemu przyłożyć i odpowiedni stopień podobieństwa do władcy przypisać. Jakaż to była miara? Edykt królewski stanowił:
Należy obwód obywatela podzielić przez 4, tak otrzymaną liczbę podnieść do kwadratu i podzielić pole przez nią. A kto tego nie zrozumie i nie wykona, to go batożkiem przystojnie oćwiczę i w ten sposób nauczę. Otrzymasz MM - Miarę Miłości, jaką do mnie, Króla Twego, czujesz, poddany mój umiłowany. Do mnie i mojej rodziny. Kto ma tę liczbę równą lub bliską jeden, znaczy, że mnie kocha. Ci, dla których jest ta liczba mała, to hultaje i muszą się poprawić w miłości do mnie, króla waszego. Dixit (co po łacinie znaczy: rzekłem).
Sprawdźmy i my, choćby ze strachu przed królewskim batożkiem. Miłościwie Panujący Król Dziesiąty Niebieski ma pole 10 razy 10, jako że bok ma długości 10. Obwód to 40. Dzielimy obwód przez 4. Otrzymujemy 10. Podnosimy do kwadratu: 100. Pole jest równe 100. Czy umiesz podzielić 100 przez 100? Umiesz.
Wynik jest równy 1. 100 procent. No, pewnie. Król jest podobny do siebie na 100 procent. A jak było dawniej? Jak było z Pomarańczowym? Miał rozmiary 8×8, czyli pole wynosiło 64. Obwód 4×8, czyli 32. Dzielimy obwód przez 4. Otrzymujemy 8. Podnosimy do kwadratu i dostajemy 64. Pole dzielimy przez 64. Znów wynik jest równy 1. Jak będzie dla innych członków dynastii? To znaczy dla innych kwadratów?
Ćwiczenie. Zapisz formułę z edyktu królewskiego ładnym wzorem. Jak najprostszym.
Wyznaczmy MM (Miarę Miłości) dla Żółtego. Nie jest to już kwadrat, a prostokąt. Pole prostokąta o rozmiarach 11×12 to 132. Oblicz bez pomocy kalkulatora. A obwód? No, jasne: 11 + 12 + 11 + 12, czyli dwa razy po 23, czyli 46. Teraz już trudniej. Podziel 46 przez 4. To 11 1/2, jedenaście i pół. Podnieś do kwadratu. Uff, trudne. Podziel pole przez otrzymaną liczbę. Ja dałem radę bez kalkulatora i otrzymałem ułamek zwykły 528/529. To prawie 1, zamień to na ułamek dziesiętny. Nie jest źle - Żółty wprawdzie nie jest kwadratem, ale jest podobny do swoich przodków na 99,8%.
Wróćmy do edyktu Najmiłościwszego Pana, z powodu którego każdy obywatel zostanie zmierzony i dostanie swoją Miarę Miłości, jaką czuje do Króla naszego Umiłowanego. Proszę ustawić się w kolejce. Mierzymy (2).
Najpierw prostokąty. Kto pierwszy? Aha, kolega Pomarańczowy. Jakie Pan ma rozmiary? Rozumiem, 8×4. To znaczy pole 32, obwód 24. Niestety, muszę obwód Pana podzielić przez 4, podnieść do kwadratu (będzie 36) i podzielić pole przez 36. Ojej, kocha Pan swego króla tylko na 88%? Proszę się bardziej skwadratowić!
Jakie MM mają kolejne prostokąty? Fioletowy, Czerwony Grubszy, Czerwony Cieńszy?
Obliczymy MM dla czarnego długiego węża na dole planszy (2). Jest on długi na całą planszę (32 guziczki) i jeszcze trochę zawinięty do góry. Ma obwód 32 + 3 + 5 + 1 + 4 + 1 + 30 + 1 + 4 + 1 + 5 + 3, uff, dodaj to może bez kalkulatora? Mnie się udało, wiesz jak? Pogrupowałem w myśli, o tak: (32 + 3 + 5) + (1 + 4 + 1 + 30) + (1 + 4 + 1 + 5 + 3) = 40 + 36 + 14 = 40 + 50 = 90.
Obwód wynosi więc 90. Jakie jest pole? Ile jest guziczków? 32 + 6 + 6 = 44. Oblicz teraz MM. 44 podzielone przez 22 i pół do kwadratu. Bez kalkulatora, dobrze? No, chyba że nie dasz rady. Powinieneś otrzymać 176/2025, czyli w przybliżeniu 0,087, tzn. osiem i pół procenta. No tak, ten wąż jest bardzo mało podobny do kwadratu.
Bez trudu poradzisz sobie ze zmierzeniem MM dla klocka z ilustracji 3. Zróbmy to razem.
Ile guziczków, takie pole. Liczymy: 53. Wiesz, jak najłatwiej? Plansza ma rozmiar 6×12, a wolnych pól jest 19, no to czerwonych jest właśnie 53.
Teraz obwód. Oj, to skomplikowane i żmudne. Policzyłem i wyszło 64. Nasz współczynnik jest teraz równy 53 dzielone przez 16 do kwadratu, 53/256, około jednej piątej. Ale chodzi mi tu o coś innego. Czy wiesz, gdzie leży wyspa Celebes? Pewnie nie. Znajdź ją w atlasie (może być w Internetowym). Zobacz: ma długą linię brzegową, Wyspa w kształcie ośmiornicy miałaby jeszcze dłuższą – w stosunku do swej powierzchni, a więc małe MM. Ośmiornice nie kochają Kwadratowego Króla. Postaram się następnym razem wytłumaczyć ci, co to jest fraktal.
Tak, tak, też na klockach lego.
Ośmiokąt kwadratem?!
Porzućmy już może naszą wyspę, chociaż będziemy do niej wracać w następnych wycieczkach. Czego się nauczyliśmy? Nauczyliśmy się pewnego sposobu mierzenia, jak bardzo są do siebie podobne figury. Podkreślam, że to tylko pewien sposób, niedoskonały i czasami bardzo mylący. Ale umiemy już coś zmierzyć. O to też chodzi w matematyce. Pomierz w ten sposób krzyże widoczne na ilustr. 2 (jasnozielony, jasnoróżową gwiazdkę, ciemnoniebieski, ciemnozielony, różowy i jasnoniebieski). Będą miały małe współczynniki MM, ale nie o to chodzi. Które będą podobne?
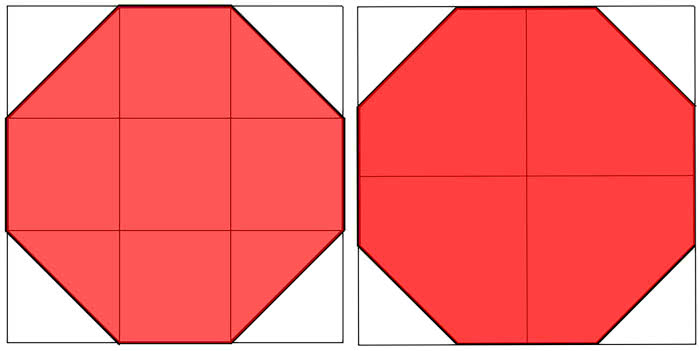
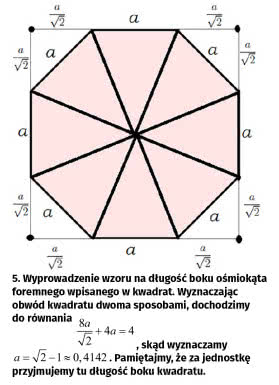
A oto interesujące i pouczające zadanie. Na jego użytek nazwijmy ośmiokąt ładnym, jeżeli ma kształt jak na ilustr. 4. Nie jest on foremny - boki mają różne długości, za to dzieli narożne kwadraciki na równe trójkąty, po przekątnej. Obwód takiego ośmiokąta równy jest 4/3 + 4/3 2 jednostek długości, a pole to 7 9 pola kwadratu. A zatem MM (Miara Miłości) to:
Najpierw sprawdźmy obliczenia. Są w porządku. Coś jednak dziwnego! Miara podobieństwa takiego ośmiokąta do kwadratu przewyższa 100 procent. Ośmiokąt jest więc doskonalszym kwadratem niż kwadrat?! Czyżby miał rację anonimowy uczeń, którego opinię wyczytałem w Internecie: matematyka to ogłupianie ludzi za pomocą cyferek!!!
W poglądzie ucznia jest ziarno prawdy. Źle użytą matematyką można ogłupić… kogoś, kto się na niej nie zna. Nóż do krojenia chleba czy kij do gry w baseball, niewłaściwie użyte, mogą… no, właśnie, wszyscy wiemy, co mogą sprawić!
Gdzie jest błąd? Jest bardzo subtelny. Wzór, wprowadzony edyktem królewskim na Wyspie Prostokątnej działa dobrze dla figur prostokątnych, przez co rozumiem to, że wszystkie ich kąty są proste. Dla innych figur podaje on nie tyle miarę "kwadratowości", co okrągłości figury - stosunku obwodu do pola, o czym postaram się napisać w następnym odcinku.
Zadania dla Czytelnika
- Oblicz MM dla sześciokąta foremnego i dla ośmiokąta foremnego.
- Jak myślisz, jaka miara podobieństwa do Cesarza jest w użyciu na Wyspie Trójkątnej, zamieszkałej przez Trójkąty? Oto portrety członków rodziny cesarskiej: Trójkątna rodzina cesarska w pełnej krasie
- Jaki kształt ma ośmiokąt znaku drogowego STOP? Czy chodzi o ten, który nazwałem ładnym, czy o ośmiokąt foremny? Jeśli nie wiesz, zbadaj to przy następnym spacerze po miejscowości, w której mieszkasz. Leniwi mogą zaś sprawdzić w Internecie.
W każdej bajce jest trochę prawdy. W mojej powiastce o Wyspie Prostokątnej znajduje się wzmianka, że być może są gdzieś istoty okrągłe, ale nikt ich nigdy nie widział. My wiemy - znamy koła, elipsy, parabole i sinusoidy. Jak bardzo podobne są do najdoskonalszej z figur płaskich - koła?
O tym już innym razem.
Michał Szurek
Zobacz także:
Dzielimy na pół - trójkąty i kwadraty
Kolorowa matematyka
Szachownica i szachy