Dzielimy na pół - trójkąty i kwadraty

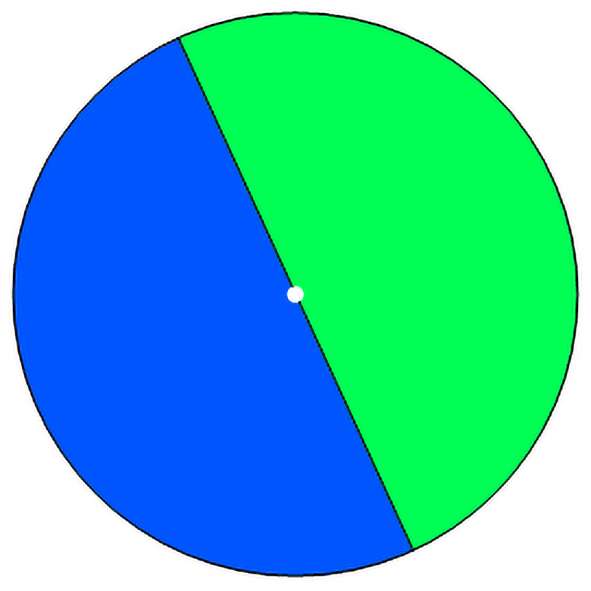
Czy umiesz podzielić koło na dwie równe połówki? Na pewno. A jak się nazywają części, które otrzymasz? Tak jest, półkola. Czy dzieląc koło jedną kreską (jednym cięciem), musisz poprowadzić tę kreskę przez środek koła? Tak. A może jednak nie musisz? Pamiętaj, że chodzi o jedno cięcie, jedną prostą kreskę.
Czy jesteś przekonany, że każda prosta przechodząca przez środek koła dzieli je na równe części? Czy jesteś przekonany, że aby podzielić koło na równe części jedną linią prostą, musimy ją poprowadzić przez środek?
Uzasadnij swoje przekonanie. A co to znaczy "uzasadnić"? Dowód matematyczny różni się od "dowodu" w sensie prawniczym. Adwokat ma przekonać sędziego, a więc sprawić, żeby Wysoki Sąd uznał, że klient był niewinny. Zawsze to było dla mnie nie do przyjęcia: jak bardzo los oskarżonego zależy od zdolności krasomówczych "papugi" (tak nieco pogardliwie określamy adwokata).
Dla matematyka samo przekonanie to za mało. Dowód musi by formalny, a teza musi być ostatnią formułą w ciągu logicznym, prowadzącym od założenia. To całkiem trudne pojęcie i rzeczywiście praktycznie nie do zrealizowania w życiu codziennym.
Może to zresztą i lepiej: procesy sądowe i wyroki oparte na "logice matematycznej" byłyby po prostu… bezduszne. Podobno coraz częściej tak się zdarza. Ale ja chcę tylko o matematyce.
Nawet w matematyce dowód formalny prostych spraw bywa kłopotliwy. Jak udowodnić oba wspomniane przekonania o podziale koła? Łatwiej jest to pierwsze, że każda prosta przechodząca przez środek dzieli koło na dwie równe części.
Można powiedzieć tak: obróćmy figurę z rys. 1 o 180 stopni. Wtedy pole zielone przejdzie na niebieskie, a niebieskie na zielone. Muszą wobec tego mieć równe pola. Jeżeli poprowadzimy linię nie przez środek, jedno z pól będzie wyraźnie mniejsze.
Trójkąty i kwadraty
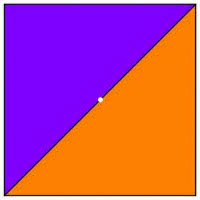
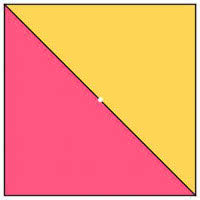
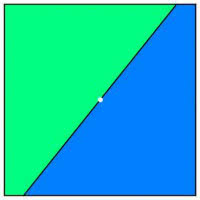
Weźmy się więc za kwadrat. Czy mamy to samo, że:
- każda prosta przechodząca przez środek kwadratu dzieli go na dwie równe części?
- jeżeli linia prosta dzieli kwadrat na dwie równe części, to musi przechodzić przez środek kwadratu?
Czy jesteśmy o tym przekonani? Sytuacja jest już inna niż dla koła (2-7).
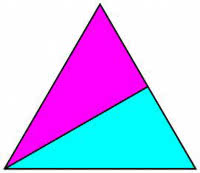
Przejdźmy do trójkąta równobocznego. Jak go rozciąć na pół? Nietrudno - wystarczy ciąć przez wierzchołek i prostopadle do podstawy (8).
Przypominam, że podstawą trójkąta może być każdy z jego boków, nawet pochyły. Cięcie przechodzi przez środek trójkąta. Czy każda prosta przechodząca przez środek trójkąta dzieli go na połowy?
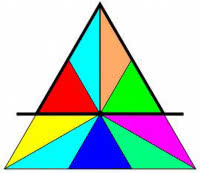
Nie! Spójrz na rys. 9. Każdy z kolorowych trójkącików ma to samo pole (dlaczego?), a zatem górna część dużego trójkąta ma cztery części, a dolna pięć. Stosunek pól wynosi nie 1:1, a 4:5.
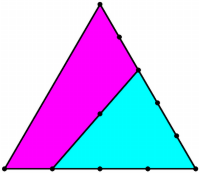
Co będzie, gdy podzielimy podstawę na, powiedzmy, cztery części i podzielimy trójkąt równoboczny cięciem przez środek oraz przez punkt w jednej czwartej podstawy? Czytelniku, czy widzisz, że na rys. 10 pole trójkąta "turkusowego" to 9/20 pola całego trójkąta? Nie widzisz? Trudno, zostawię Ci to jako zadanie do rozwiązania.
Pierwsze pytanie - wyjaśnij, jak to jest: dzielę podstawę na cztery równe części, prowadzę prostą przez punkt podziału i środek trójkąta, a na przeciwległym boku otrzymuję dziwny podział, w stosunku 2:3? Dlaczego? Czy umiesz to obliczyć?
A może jesteś, Czytelniku, tegorocznym maturzystą? Jeśli tak, to proszę, wyznacz, przy jakim położeniu prostych stosunek pól jest jak najmniejszy? Nie umiesz? Nie mówię, że masz to rozwiązać natychmiast. Daję Ci dwie godziny.
Jeśli nie rozwiążesz, to… , no cóż, życzę Ci i tak powodzenia na maturze. Wrócę jeszcze do tego tematu.
Obudzić samodzielność
"Czy umiecie się dziwić?" To tytuł książki, wydanej dawno temu przez miesięcznik matematyczno-fizyczno-astronomiczny "Delta". Spójrz na świat dookoła. Dlaczego istnieją rzeki o dnie piaszczystym (przecież woda powinna od razu wsiąknąć!).
Dlaczego chmury unoszą się w powietrzu? Dlaczego samolot leci? (powinien od razu spaść). Dlaczego w górach niekiedy jest cieplej na szczytach niż w dolinach? Dlaczego na półkuli południowej Słońce w południe jest na północy? Dlaczego suma kwadratów przyprostokątnych równa się kwadratowi przeciwprostokątnej? Dlaczego ciało zanurzone w wodzie traci pozornie na wadze tyle, ile waży wyparta przez nie woda?
Pytania, pytania, pytania. Nie wszystkie od razu stosują się do codzienności, ale prędzej czy później będą. Czy doceniasz, Czytelniku, znaczenie ostatniego pytania (o wodzie wypartej przez zanurzone ciało)? Po zrozumieniu tego pewien starszy pan biegł nago po mieście, krzycząc "Eureka, znalazłem!" Nie tylko odkrył prawo fizyczne, ale udowodnił w ten sposób, że złotnik króla Herona był fałszerzem!!! Zajrzyj po szczegóły w czeluść Internetu.
Popatrzmy teraz na inne figury.
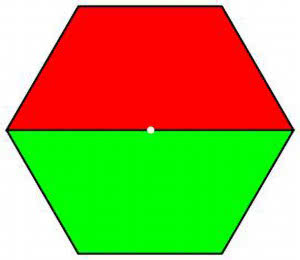
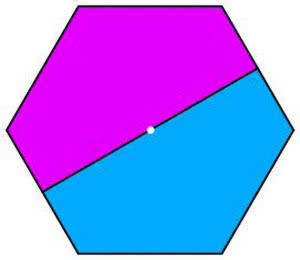
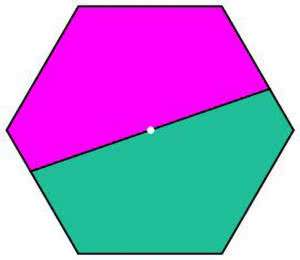
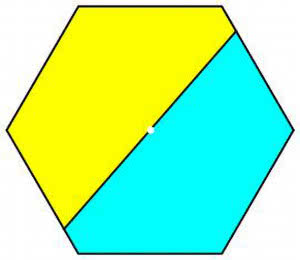
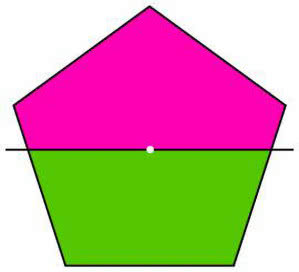
Sześciokąt (11-14). Czy każda prosta przechodząca przez jego środek dzieli go na połowy? Czy prosta dzieląca sześciokąt na połowy musi przechodzić przez środek?
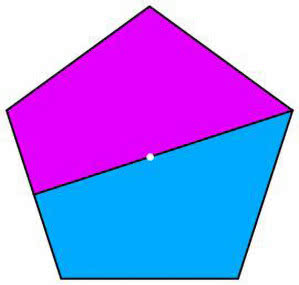
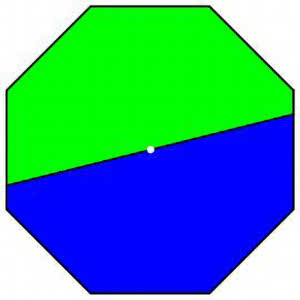
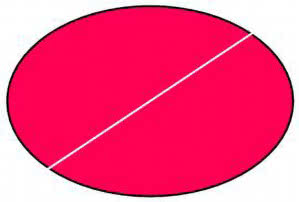
A co dla pięciokąta (15, 16)? Ośmiokąta (17)? A dla elipsy (18)?
Jedną z wad nauki szkolnej jest to, że uczymy w "dziewiętnastowieczny sposób" - dajemy uczniom zadanie i oczekujemy, że je rozwiążą. Co w tym złego? Nic - oprócz tego, że za kilka lat nasz uczeń będzie musiał nie tylko reagować na polecenia, które "dostał" od kogoś, ale sam dostrzegać problemy, formułować zadania, poruszać się po obszarze, gdzie nikt inny jeszcze nie dotarł.
Mam tak wiele lat, że marzy mi się taka stabilność: "naucz się, Jasiu, robić buty, a jako szewc będziesz miał zatrudnienie do końca życia". Wykształcenie jako przejście do wyższej kasty. Procenty do końca życia.
Ale jestem na tyle "nowoczesny", że wiem, iż muszę przygotować swoich uczniów do zawodów, których... jeszcze nie ma. Najlepsze, co mogę i co możemy zrobić, to pokazywać uczniom: CZY UMIECIE SIĘ DZIWIĆ? Nawet na poziomie matematyki elementarnej.
Zobacz także:
Dzielenie "na pół"
Bryły: znane, nieznane, nieistniejące i dające do myślenia
Jak to dobrze, że dzieli się przez 2