Jak to dobrze, że dzieli się przez 2

Siedzieliśmy z kolegą, polonistą i socjologiem, Andrzejem, nad pięknym jeziorem suwalskim Mauda. Lipiec był zimny tego roku. Nie pamiętam już, dlaczego opowiedziałem znany dowcip o motocykliście, który stracił panowanie nad pojazdem, uderzył w drzewo, ale przeżył. W karetce zaś majaczył, "jak to dobrze, że chociaż dzieli się przez dwa". Lekarz dobudził go i zapytał, o co chodzi, co się ma dzielić, czy nie dzielić przez dwa. Odpowiedź brzmiała: mv2.
Andrzej śmiał się długo, ale potem zapytał nieśmiało, o co chodzi z tym mv2. Wytłumaczyłem, że E = mv2/2 to jest wzór na energię kinetyczną, dość oczywisty, jeżeli zna się rachunek całkowy, ale nie za bardzo rozumiał. Po kilku dniach poprosił, już listownie, o takie wyjaśnienie, żeby trafiło do niego, polonisty. Na wszelki wypadek powiedziałem, że nie ma królewskich dróg w geometrii (tak rzekł Arystoteles do swojego królewskiego ucznia, Aleksandra Wielkiego). Wszyscy muszą męczyć się tak samo. Oj, czy to prawda? Wprawny przewodnik górski poprowadzi przecież klienta najłatwiejszą drogą.
mv2 dla opornych
Andrzeju. Byłbym niepocieszony, gdybyś stwierdził, że poniższy tekst jest dla Ciebie za trudny. Moje zadanie: wyjaśnić Ci, o co chodzi z tym mv2. W szczególności, dlaczego kwadrat i dlaczego dzielimy przez dwa.
Widzisz: mv to pęd, a energia to całka pędu. Proste?
Tak by Ci odpowiedział fizyk. A ja… Ale na wszelki wypadek, tytułem wstępu, przypomnienie dawnych czasów. Uczono nas tego w szkole podstawowej (gimnazjów jeszcze nie było).
Dwie wielkości są wprost proporcjonalne, jeżeli zwiększenie albo zmniejszenie jednej powoduje zwiększenie albo zmniejszenie drugiej, zawsze w tym samym stosunku.
Na przykład:
X 1 2 3 4 5 6 7 8 9
Y 5 10 15 20 25 30 35 40 45
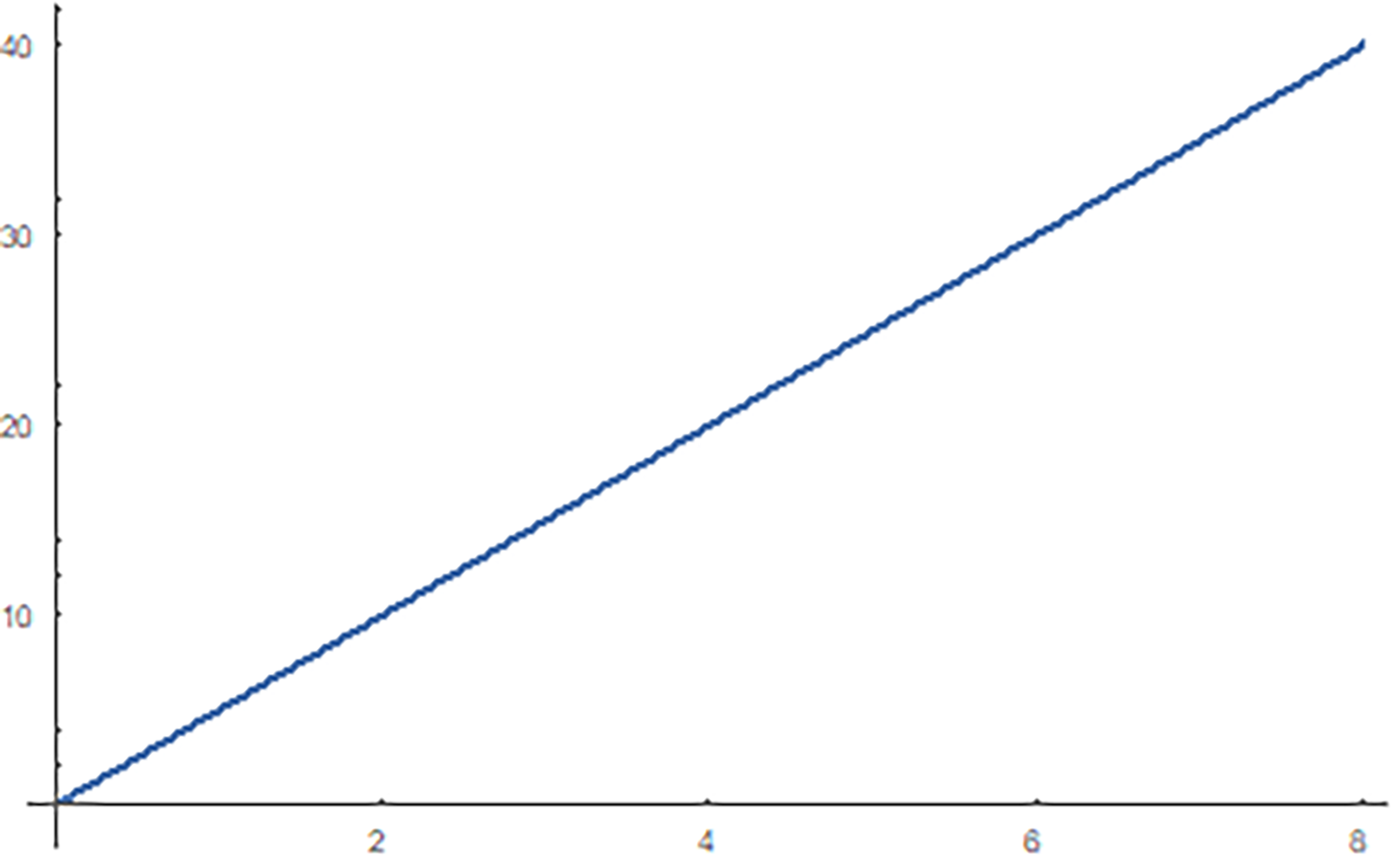
W tym przypadku Y jest zawsze pięć razy większe niż X. Mówimy, że współczynnik proporcjonalności jest równy 5. Wzór opisujący tę zależność to y = 5x. Możemy narysować wykres linii prostej y = 5x (1). Wykresem proporcjonalności prostej jest jednostajnie wznosząca się linia prosta. Równym przyrostom jednej zmiennej odpowiadają równe przyrosty drugiej. Dlatego bardziej matematyczna nazwa takiej zależności to: zależność liniowa. Ale z tego nie będziemy korzystać.
Poświęćmy teraz chwilę uwagi energii. Co to jest energia? Zgodzimy się, że jest to jakaś ukryta siła. "Nie mam siły na porządki" to niemal to samo, co "Nie mam energii do sprzątania". Energia to ukryta siła, która drzemie w nas, a nawet w rzeczach, i dobrze jest ją ujarzmić, by nam służyła, a nie powodowała destrukcji. Nabieramy energii, np. ładując akumulatory.
Jak mierzyć energię? To proste: miarą pracy, którą może za nas wykonać. W jakich jednostkach mierzymy energię? Właśnie w tych samych, co pracę. Ale na użytek tego artykułu będziemy ją mierzyć w… metrach. Jak to?! Zobaczymy.
Przedmiot zawieszony wysoko, na wysokości h nad poziomem, ma energię potencjalną. Ta energia wyzwoli się, gdy przetniemy sznurek, na którym wisi ciało. Wtedy spadnie ono i wykona pewną pracę, choćby było nią tylko stworzenie dziury w ziemi. Gdy nasz przedmiot leci, ma energię kinetyczną, energię pochodzącą od samego ruchu.
Zgodzimy się łatwo, że energia potencjalna jest proporcjonalna do wysokości h. Wniesienie towaru na wysokość 2h zmęczy nas dwa razy więcej, niż wniesienie go na wysokość h. Winda, gdy zawiezie nas na piętnaste piętro, zużyje trzy razy tyle prądu co na piąte… (po napisaniu tego zdania zdałem sobie sprawę, że to nieprawda, bo winda oprócz ludzi dźwiga jeszcze własną masę, i to niebagatelną - aby uratować przykład, trzeba zastąpić windę przez np. dźwig budowlany). Podobnie jest z proporcjonalnością energii potencjalnej do masy ciała. Transport 20 ton na wysokość 10 m zużywa dwa razy tyle prądu, co 10 ton na 10 m. Możemy to wyrazić wzorem E ~ m h, gdzie tylda (tj. znak ~) jest znakiem proporcjonalności. Dwa razy większa masa i dwa razy większa wysokość to cztery razy większa energia potencjalna.
Nadawanie ciału energii potencjalnej przez podnoszenie na pewną wysokość nie miałoby miejsca, gdyby nie siła grawitacji. To dzięki niej wszystkie ciała spadają na ziemię (na Ziemię). Działa ta siła tak, że ciała dostają stałego przyspieszenia. Co to znaczy "stałe przyspieszenie"? To znaczy, że spadające ciało zwiększa swoją prędkość miarowo, jednostajnie - tak, jak samochód ruszający z miejsca. Jedzie coraz szybciej, ale przyspiesza w stałym tempie. Za chwilę zobaczymy to na przykładzie.
Przypomnę tylko, że przyspieszenie ziemskie oznaczamy przez g. Wynosi ono ok. 10 m/sek2. Znów można mieć pytanie: co to za dziwna jednostka - kwadrat sekundy? Należy to jednak rozumieć inaczej: w każdej sekundzie prędkość spadającego ciała zwiększa się o 10 m na sekundę. Jeśli w pewnym momencie porusza się z prędkością 25 m/sek., to po sekundzie ma już prędkość 35 (m/sek.). Zrozumiałe też, że mamy tu na uwadze ciało, któremu nie za bardzo przeszkadza opór powietrza.
Musimy teraz rozwiązać pewne zadanie arytmetyczne. Weźmy pod uwagę opisane przed chwilą ciało, które w pewnej chwili ma prędkość 25 m/sek., a po sekundzie 35. Jaki dystans przebędzie w ciągu tej sekundy? Kłopot w tym, że prędkość jest zmienna i do prawidłowych obliczeń potrzebny jest rachunek całkowy. Potwierdzi on jednak to, co czujemy intuicyjnie: wynik będzie taki sam, co dla ciała poruszającego się jednostajnie z prędkością średnią: (25 + 35)/2 = 30 m/sek. - a zatem 30 m.
Przenieśmy się na chwilę na inną planetę, o innym przyspieszeniu, np. 2g. Jest jasne, że tam energię potencjalną zyskujemy dwa razy szybciej - przez wzniesienie ciała na dwa razy mniejszą wysokość. Energia jest zatem proporcjonalna do przyspieszenia na danej planecie. Przyjmijmy za wzorcowe przyspieszenie ziemskie. I tak przecież nie znamy cywilizacji, żyjącej na planecie o innej sile grawitacji. W ten sposób dochodzimy do wzoru na energię potencjalną: E = gmh.
Przetnijmy teraz sznurek, na którym zawiesiliśmy kamień o masie m na wysokości h. Kamień spada. Gdy uderzy w ziemię, wykona pracę - kwestią inżynierską jest wykorzystanie jej na nasz pożytek.
Narysujmy wykres: ciało o masie m spada w dół (tym, którzy zarzucą mi sformułowanie, że przecież do góry spadać nie może, odpowiem, że mają rację i właśnie dlatego napisałem, że w dół!). Wystąpi kolizja oznaczeń: litera m będzie oznaczać zarówno metry, jak i masę. Ale domyślimy się, co kiedy. Teraz popatrzmy na wykres poniżej i komentarz do niego.
Niektórzy pomyślą: to tylko podejrzane sztuczki liczbowe. Ale sprawdźmy: jeżeli ciało startuje do góry z prędkością 50 km/godz., to osiąga wysokość 125 m - czyli w punkcie, w którym się na nieskończenie krótką chwilę zatrzyma, będzie mieć energię potencjalną 1250 m, a to jest też mv2/2. Gdybyśmy wystrzelili ciało z prędkością 40 km/godz., zaleciałoby na 80 m, znów mv2/2. Teraz chyba nie mamy wątpliwości, że to nie jest przypadek. Odkryliśmy jedno z newtonowskich praw ruchu! Trzeba było tylko wykonać eksperyment myślowy (o, przepraszam, najpierw wyznaczyć przyspieszenie ziemskie g – według legendy zrobił to Galileusz, zrzucając przedmioty z wieży w Pizie, już wtedy krzywej) i co najważniejsze: mieć intuicję liczbową. Wierzyć, że dobry Pan Bóg stworzył świat, stosując się do praw matematycznych (które może sam przedtem wymyślił). Może też pomyślał sobie: a, zrobię takie prawa fizyki, żeby musieli dzielić przez dwa. To i pół biedy, większość stałych fizycznych jest tak niesamowicie dziwna, że można podejrzewać Stwórcę o poczucie humoru. Dotyczy to i matematyki, ale nie o tym dzisiaj.
Kilkanaście lat temu w Tatrach alpiniści wzywali pomocy, z jednej ze ścian nad Morskim Okiem. Był luty, zimno, krótki dzień, zła pogoda. Ratownicy dotarli do nich dopiero następnego dnia w południe. Alpiniści byli już wymrożeni, głodni, bez sił. Ratownik podał pierwszemu z nich termos z gorącą herbatą. "Z cukrem?" zapytał ledwo słyszalnym głosem alpinista. "Tak, z cukrem, witaminami i środkiem wzmacniającym krążenie". "Dziękuję, z cukrem nie pijam!", odrzekł alpinista i zemdlał. Chyba podobne, stosowne poczucie humoru wykazał nasz motocyklista. Ale dowcip byłby głębszy, gdyby westchnął powiedzmy tak: "ach, gdyby nie ten kwadrat!".
Co bowiem mówi wzór, zależność E = mv2/2? Co powoduje "kwadrat"? Co jest cechą zależności "kwadratowej"? To, że np. dwukrotne zwiększenie przyczyny powoduje czterokrotne zwiększenie skutku; trzykrotne - dziewięciokrotne, czterokrotne - szesnastokrotne. Energia, jaką mamy, jadąc 20 km/godz., jest czterokrotnie mniejsza niż dla 40, a szesnastokrotnie niż dla 80! Zresztą wyobraźmy sobie skutki zderzenia przy prędkości 20 km/godz. ze skutkami kolizji przy 80 km/godz. Bez żadnych wzorów widać, że o wiele, wiele większe. Zależność skutków rośnie kwadratowo względem prędkości, a dzielenie przez dwa tylko trochę to łagodzi.
* * *
Wakacje już poza nami. Od kilku lat pisywałem artykuły "na nowy rok szkolny". Teraz… nie mam siły. Musiałbym pisać o reformie edukacji, która ma również dobre strony, ale decyzja została podjęta ze względów niemerytorycznych przez osoby, które nadają się do tego, jak ja do baletu (mam znaczną nadwagę i ponad 70 lat).
Natomiast niejako z obowiązku odniosę się do kolejnego przejawu nieznajomości podstawowej matematyki wśród dziennikarzy. Wprawdzie nic nie przebije pewnej dziennikarki z Olsztyna, która poświęciła długi artykuł sprawie oszukiwania konsumentów przez producentów. Otóż, pisała dziennikarka, na opakowaniu masła podano zawartość tłuszczu w procentach, ale nie wyjaśniono, czy na kilogram, czy na całą kostkę...
Nieścisłość, jaką napisał dziennikarz A.B. (inicjały zmyślone) w "Tygodniku Powszechnym" z 30 lipca b.r. jest bardziej subtelna. Podał on, że wg badań CBOS aż 48% osób uważających się za bardzo religijne akceptuje pewną postawę X (mniejsza o to, o co chodzi, to nieistotne), zaś popiera X 41% tych, co kilka razy w tygodniu uczestniczą w praktykach religijnych. Oznacza to, pisze autor, że ponad dwie piąte najbardziej aktywnych katolików nie uznaje X. Próbowałem długo dociec, skąd autor wziął owe dwie piąte i… nie rozumiem. Błędu formalnego o tyle nie ma, że istotnie, matematycznie rzecz biorąc ponad dwie piąte respondentów jest przeciw X. Tyle, że równie dobrze można napisać, że ponad połowa (100 – 48 = 52).