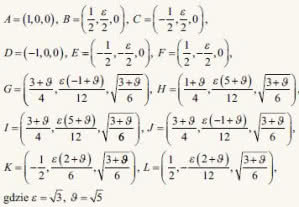Bryły: znane, nieznane, nieistniejące i dające do myślenia

No, dobrze, tyle na razie o tym, co za oknem. Co do konferencji. Przyjemnie jest widzieć nauczycieli, którym po prostu się chce, którym zależy na tym, by ich uczniowie byli dobrze wykształceni i przyzwoici. Artykuł ten jest streszczeniem referatu, który miałem wygłosić w Sielpi - w ładnej okolicy na pograniczu świętokrzyskiego i łódzkiego.
Wszechświat ośmiościanów
Każdy wie, co to jest bryła. Można powiedzieć, że jest to po prostu figura przestrzenna. W języku potocznym może być nieregularna: bryłka soli, bryła węgla, ale w architekturze mówimy przecież o "interesującej bryle" pewnej budowli. Zawsze jest w niej pewna "matematyczność", bo nawet jeśli to ma być "chaos", to zaplanowany wg jakiegoś wzoru.
Tak, tak - chaos nie bierze się z przypadkowości. Nie należy mieszać tych pojęć. Przypadkowymi procesami rządzą zdumiewająco ścisłe prawa, a z kolei nawet prosty proces, powtarzany wiele razy, da strukturę chaotyczną. Równie dobrymi przykładami są tasowanie kart i zagniatanie ciasta.
Wiele pięknej geometrii znajduje się w najprostszych bryłach - wielościanach. Jak sama nazwa wskazuje, wielościany mają wiele ścian. Ściany są wielokątami. A więc wielościan ma dużo kątów: płaskich i przestrzennych.
Czy może mieć tylko jeden kąt? Dokładniej: po jednym kącie płaskim i jednym przestrzennym?
Takich brył jest tylko pięć: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan.
Gdybym pisał ten artykuł dwadzieścia lat temu, musiałbym zamieścić rysunki tych brył. A teraz? Wiesz dobrze, lepiej ode mnie, młody Czytelniku, że jeżeli jedziesz tramwajem, leżysz na plaży, albo popijasz niezdrowego hamburgera niezdrową coca-colą, masz w zasięgu smartfona wszystko. Obrazy wielościanów foremnych także. Wiesz co? Zrób mi przyjemność i zajrzyj tam! Obejrzyj te wielościany, a ja zaoszczędzę trochę miejsca. Czy wiesz, że te bryły odkryli już Grecy, prawie 2500 lat temu?
Matematycznie najprostszą bryłą jest czworościan, ale najbardziej popularną stanowi sześcian. Prosty, ale ciekawy. Co decyduje, że jest tak popularny, tak często wykorzystywany w budownictwie, zdobnictwie, transporcie i tak dalej? Nie ma na to jednoznacznej odpowiedzi, ale na pewno najważniejsze jest to, że z prostopadłościanów łatwo budować. Równomiernie ustawione sześciany wypełniają przestrzeń. Inne wielościany foremne są mało przydatne w technice.
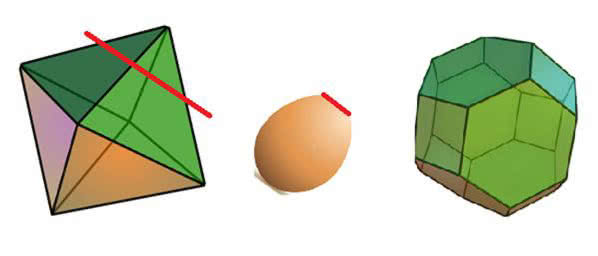
Jedną z ciekawszych brył jest tzw. ośmiościan ścięty. Kto zobaczył ośmiościan, może sobie teraz wyobrazić, że ścinamy jego naroża, tak w poprzek, jak czubek jajka na miękko. Oto, co powstaje (1).
Zadanie. Zbuduj, jakie potrafisz, bryły, używając tylko sześciokątów i kwadratów.
Zawsze zastanawiało mnie, w jaki sposób starożytni Grecy dochodzili do swoich prawd geometrycznych. Specjaliści twierdzą, że bryły (w szczególności foremne) dostawali jako kryształy. Być może. Prawdopodobnie ośmiokąta ściętego tak nie poznali. Dopiero w 1842 r. odkryto minerał, krystalizujący w ten sposób.
Teraz ja muszę zajrzeć do Wikipedii…
Ów kryształ nazywa się fojazyt, a jego wzór to (Na2, Ca, Mg)3-4[(Si, Al)24O48] x 32 H2O. Nazwa upamiętnia francuskiego geologa i wulkanologa, którym był Bartholomeo Faujas de Saint Fond (1741-1819).
Można policzyć, że ośmiościan ścięty ma 24 wierzchołki, 36 krawędzi i 14 ścian. Obliczmy: 24–36+14=2. Porównajmy te liczby z podobnymi dla czworościanu:
4 wierzchołki, 6 krawędzi, 4 ściany: 4–6+4=2 i sześcianu: 8–12+6=2.
Zawsze to samo. Liczba ścian plus liczba wierzchołków przewyższa o 2 liczbę krawędzi. Odkrył to Leonard Euler (1707-1783). Zawsze, dla każdego wielościanu wypukłego.
Ośmiościan ścięty jest bryłą, która w pewnym sensie mnie przeraża. Otóż można nią wypełniać całą przestrzeń - podobnie jak sześcianami, bez luk i naddatków. Gdy ludzkość zmuszona będzie opuścić Ziemię, być może wzniesiemy sobie takie właśnie kosmiczne miasta.
Ośmiościany - żeby uciec od nieznośnej symetrii sześciennej. Ośmiościany ścięte - bo łatwiej je budować z powtarzalnych segmentów. Powstaną olbrzymie kratowe budowle, z długimi tunelami na przestrzał, w trzy przestrzenne strony świata. Trochę przerażające, prawda? Zresztą tak się chyba muszą dzisiaj czuć mieszkańcy albo pracownicy w superwieżowcach w Dubaju. Co prawda nie wiem, nie byłem i się nie wybieram.
Pogadanki o czternastce
Skoro jestem przy głosie, to rozgadam się teraz o liczbie 14. Zebrałem kiedyś trochę ciekawostek i szkoda, żeby się zmarnowały.
Zabawne - z wczesnej młodości zapamiętałem pewną fotografię z albumu z wczesnych lat pięćdziesiątych, kiedy Warszawa była jeszcze morzem gruzów z wysepkami nowych osiedli. Mokotów był stosunkowo mało zniszczony. Na skrzyżowaniu Alei Niepodległości z Rakowiecką skręcał w lewo tramwaj numer 14.
Podpis głosił, że niedługo będzie tu metro… (i rzeczywiście, już po czterdziestu latach było). Do warszawskiej linii tramwajowej numer 14 mam od sześćdziesięciu lat duży sentyment. O linii trolejbusowej 56 zapowiadam inny artykuł.
Klasyczny sonet włoski ma czternaście wersów (rymy abba, abba, cdc, dcd) - przypomnijmy sobie np. "Sonety Krymskie", autorstwa pewnego studenta Wydziału Matematycznego Uniwersytetu w Wilnie (nie zrobił kariery w matematyce i słuch o nim zaginął).
William Shakespeare napisał 154=14∙11 sonetów (miały one nieco inną formę niż klasyczne, włoskie). Po czternaście lat miały Zosia Horeszkówna i Julia Capuletti, kiedy weszły na karty literatury, ale związek tego z popularnymi w anglosaskiej kulturze Walentynkami (14 lutego) jest przypadkowy.
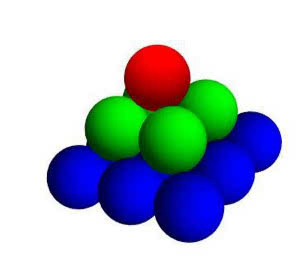
Przechodząc do matematyki, odnotujmy, że 14 jest sumą kwadratów trzech pierwszych liczb naturalnych: 12+22+32=14. Pokazują to piramidki na ilustr. 5 i 6.
Widzicie Państwo, jak ciekawa jest liczba 14. A zatem do roboty!
Zadanie. Zbudować bryłę o czternastu ścianach. Jedną już mamy opanowaną: ośmiościan ścięty, kryształ fojazytu. Ogłaszam dwa konkursy: na najładniejszą bryłę i na najbardziej "śmieszną", cokolwiek to znaczy.
Tu docisnąć, tam naciągnąć…
Rezultat powyższych konkursów przeprowadzonych w trakcie konferencji przeszedł wszelkie oczekiwania (8). Omówienie zajęłoby ćwierć objętości naszego miesięcznika. Gdzieś z tyłu wśród stworzonych wielościanów leżała bryłka, którą zaproponowałem nazwać Bryłą im. Reformy Edukacji (9). Dlaczego?
Po kolei.
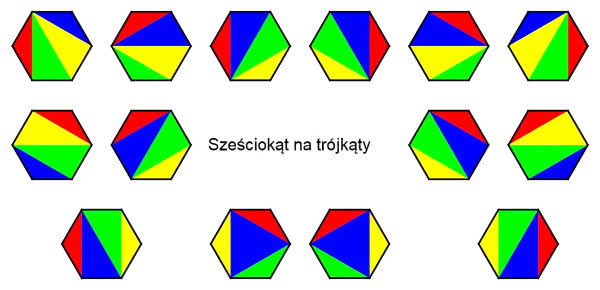
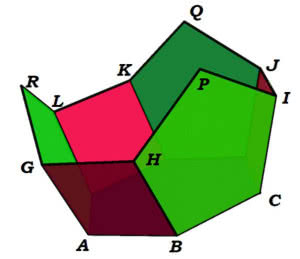
Zróbmy sobie ładną bryłkę. Wykonujemy najpierw podstawę i ściany boczne - sześciokąt okładamy na przemian pięciokątami i kwadratami (10). Zaginamy je do góry i otrzymujemy "koronę" - gdybyśmy używali tylko pięciokątów, mielibyśmy połówkę dwunastościanu. Możemy łatwo obliczyć współrzędne wierzchołków tej "korony". Stosowne wzory zamieszczam na końcu artykułu - gdyby ktoś chciał sprawdzić moje rachunki.
Koronę można domknąć na różne zresztą sposoby. Minimalistyczny sposób wygląda następująco:
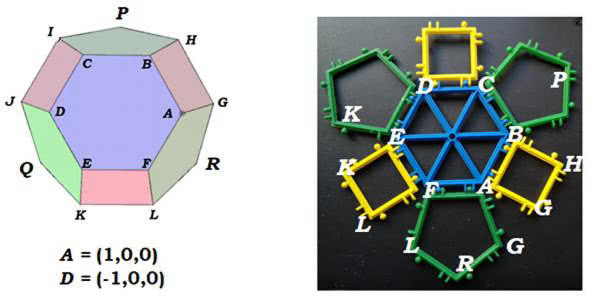
punkty P, Q, R są wierzchołkami trójkąta równobocznego o boku 2. Po wstawieniu tego trójkąta jako "daszka" zobaczymy jeszcze trzy "dziury": RGHP, PIJQ i QKLR - wszystkie w kształcie trapezów równobocznych o bokach 2,1,1,1. Każdy z tych trapezów złożony jest z czterech trójkątów równobocznych.
Doklejamy.
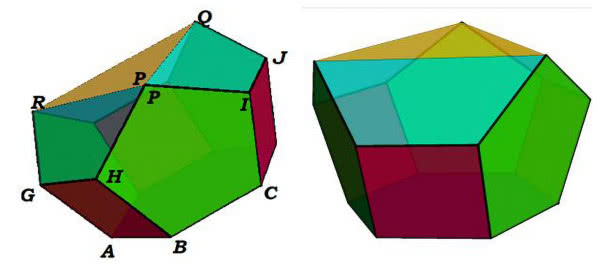
Oto i co powstało - zgrabny jedenastościan (12). Składają się na niego sześciokąt foremny, trzy kwadraty, trzy pięciokąty foremne (o boku 1), jeden trójkąt równoboczny o boku 2 i trzy trapezy równoramienne o bokach 2,1,1,1.
Wyobrażam sobie, że właśnie tak mógł wyglądać domek na Księżycu, w którym mieszkali Pirx i Langner (Stanisław Lem, "Odruch warunkowy"). Stanisław Lem (1921-2006) zasługiwał na literacką Nagrodę Nobla. Prawdopodobnie był jednak niezrozumiany i trudno przetłumaczalny na niesłowiańskie języki. Ukrywał pod kostiumem "kosmicznym" codzienne, zwykłe problemy nas wszystkich.
Będę więc opisaną konstrukcję nazywać domkiem Pirxa. Solidny, ergonomiczny domek, przylepiony do księżycowej skały (jak w cytowanym opowiadaniu).
Pentagonalna podstawa, płaski trójkątny daszek i ukośne trapezoidalne świetliki - okna u góry. Urozmaicony parter - na przemian ściany kwadratowe i pięciokątne. Może nie tak, jak w dworkach szlacheckich, ale całość tchnie trudno opisywalną nostalgią.
Domek Pirxa da się nietrudno przerobić na pożądany w zadaniu czternastościan, doklejając czworościan foremny (13) o podstawie PUV, gdzie U jest środkiem odcinka PQ, a V środkiem odcinka PI. W tej dobudówce znakomicie pomieści się radioteleskop, skierowany na Ziemię, naszą jedyną planetę. Można dostawić na dachu dzióbek (mały lub duży) i w ogóle zabawa przednia!
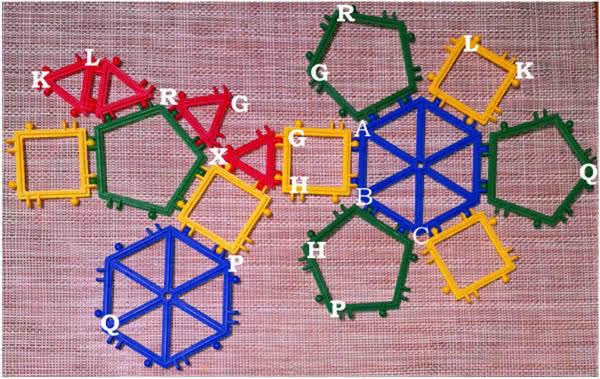
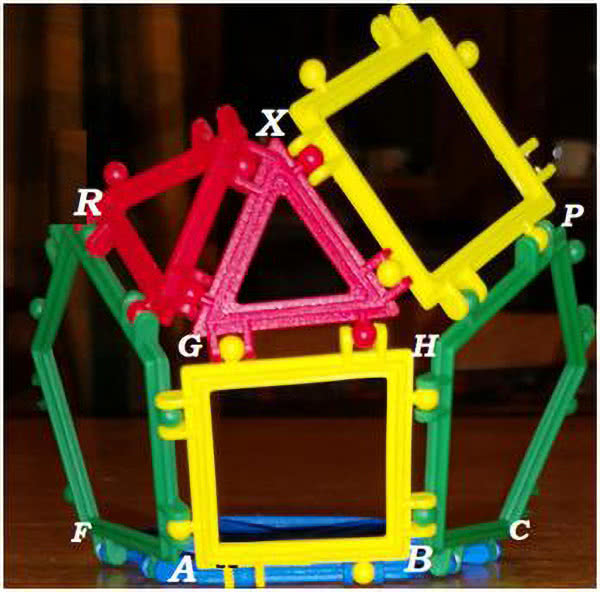
Wróćmy w tym momencie do naszej konferencji w Sielpi. Kilkuosobowa grupa postanowiła inaczej wykończyć koronę z ilustr. 11. Zamiast długiego i niestrawnego opisu załączę siatkę i fotografię, co z tego wyszło (14). Proszę spróbować samodzielnie, z klocków albo z kartonu. Trochę trudno złożyć, ale jak się dociśnie, to powstanie interesująca bryła (9).
I teraz "jądro sedna" artykułu: taka bryła nie istnieje!
Jak to nie istnieje? Przecież widzimy jej model.
No tak, ale plastik da się trochę naciągać. Tu przygiąć, tam odgiąć.
Matematyczny dowód nieistnienia takiej bryły jest prosty, choć wymaga pewnych rachunków. Wybiorę jeden z narożników (9, 15). Punkt X jest odległy od R, G, H o jednostkę, a od punktu P o pierwiastek z 2.
Niech X=(x, y, z). Wyznaczymy odległości punktu X od R, G, H, P. Okaże się, że odpowiedni układ równań jest sprzeczny. Takiego punktu nie ma. Bryła istnieje tylko dzięki sprytnym naciągnięciom. Jak się dobrze przypatrzeć, widać, że ABGH to "naciągany kwadrat".
Czy teraz przyjmujecie, Czytelnicy, pomysł, żeby tę bryłę uhonorować mianem "Bryły imienia Reformy Edukacji"? I jedna, i druga wygląda ładnie na papierze, ale w praktyce złożyć się nie da.
Pytanie do byłej pani minister, Anny Zalewskiej: jak się Pani czuje w Brukseli? To miłe uczucie, tak wszystko zepsuć i uciec, prawda? To stara bolszewicka taktyka.
Przygotować na niewiadome
Zostawiłem na koniec bardzo ważne zagadnienie. Uważny Czytelnik, tej czy innej opcji politycznej, zapyta trzeźwo: po co uczyć dzieci o tym, o czym tutaj opowiadałem? Czy nie należy uczyć tego i tylko tego, co się w życiu przyda?
Mój dziadek był szewcem. Bardzo dobrym. Wyuczył się porządnie swego fachu; po jego buty schodzili się ludzie z całej okolicy. Dziadek wiedział, że ma dobry zawód i zapewnione utrzymanie na całe lata. Świat był taki stabilny…
Dla dziadka skończył się w 1914 r. Przeżył wojnę, ale wrócił z gruźlicą. W Niepodległej mój ojciec startował od zera.
Dziś stają przed nami uczniowie, ba - nasze dzieci, a my nie znamy nawet nazw zawodów, które będą wykonywać w nieodległej przyszłości. Co im będzie potrzebne?
"Co im się w życiu przyda"? Nie wiemy. A przygotować ich do tego musimy. I nauczyciele właśnie to robią, a nie - jak twierdzi wielu przekonanych przez propagandę rządzącej koalicji - tylko wyciągają pieniądze z budżetu. W potępionym dziś ze względów ideologicznych wierszu Juliana Tuwima "Do córki w Zakopanem" jest fragment:
"Kłaniaj się wiejskim nieznanym nauczycielkom, Brnącym przez śniegi do szkółek w mrozy siarczyste".
Ja się kłaniam.