Nowa matematyka maszyn? Eleganckie wzory i bezradność

Według niektórych ekspertów maszyny potrafią wymyślać lub, jak kto woli, odkrywać, całkiem nową matematykę, jakiej my ludzie nigdy nie widzieliśmy i nie wpadlibyśmy na nią. Inni twierdzą, że maszyny same niczego nie wymyślają, potrafią jedynie inaczej przedstawiać wzory, które i tak znamy, zaś z niektórymi problemami matematycznymi w ogóle sobie nie radzą.

Grupa naukowców z Instytutu Technion w Izraelu i Google zaprezentowała niedawno zautomatyzowany system wysuwania twierdzeń, który nazwali Ramanujan Machine, na cześć matematyka Srinivasy Ramanujana, który opracował tysiące innowacyjnych formuł w teorii liczb, nie mając prawie żadnego formalnego wykształcenia. Stworzony przez badaczy system wyprowadził serię oryginalnych i ważnych wzorów na uniwersalne stałe, które pojawiają się w matematyce. Praca na ten temat została opublikowana w "Nature".

Jeden z wzorów opracowanych przez maszynę może być użyty do obliczania wartości uniwersalnej stałej, zwanej liczbą Catalana, bardziej efektywnie niż przy zastosowaniu wcześniej znanych formuł odkrytych przez człowieka. Uczeni twierdzą jednak, że Maszyna Ramanujana nie ma na celu przejęcia matematyki z rąk ludzi, lecz raczej ma oferować pomoc dla matematyków. Jednak nie znaczy to, że ich system jest pozbawiony ambicji. Jak piszą, Maszyna "próbuje naśladować intuicję matematyczną wielkich matematyków i dostarczać wskazówek do dalszych poszukiwań matematycznych".

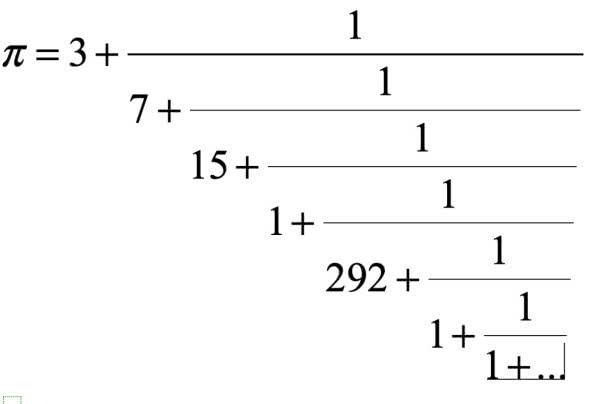
System tworzy przypuszczenia dotyczące wartości uniwersalnych stałych (takich jak Pi), zapisane w postaci eleganckich formuł, zwanych ułamkami ciągłymi lub też ułamkami łańcuchowymi (1). Nazywa się tak sposób wyrażenia liczby rzeczywistej w postaci ułamka w specjalnej postaci lub granicy takich ułamków. Ułamek ciągły może być skończony lub mieć nieskończenie wiele ilorazów częściowych a_i/b_i; ułamek A_k/B_k otrzymany przez odrzucenie w ułamku ciągłym ilorazów częściowych, począwszy od (k+1)-ego, nazywa się k-tym reduktem i może być obliczony za pomocą wzorów: A_-1=1,A₀=b₀, B_-1=0, B₀=1, A_k=b_kA_k-1+a_kA_k-2, B_k=b_kB_k-1+a_kB_k-2; jeżeli ciąg reduktów jest zbieżny do skończonej granicy, to ułamek ciągły nazywa się zbieżnym, w przeciwnym przypadku - rozbieżnym; ułamek ciągły nazywa się arytmetycznym, jeżeli a_i=1, b₀ jest całkowite, b_i (i>0) - naturalne; ułamek ciągły arytmetyczny jest zbieżny; każda liczba rzeczywista rozwija się na ułamek ciągły arytmetyczny, który jest skończony tylko dla liczb wymiernych.

1. Przykład zapisu liczby Pi w postaci ułamka ciągłego

Algorytm Maszyny Ramanujana wybiera dowolne stałe uniwersalne dla lewej strony i dowolne ułamki ciągłe dla prawej, a następnie oblicza każdą stronę osobno z pewną dokładnością. Jeśli obie strony wydają się pokrywać, wielkości są obliczane z większą precyzją, w celu upewnienia się, że ich zgodność nie jest przypadkiem wynikającym z niedokładności. Co istotne, istnieją już wzory pozwalające obliczyć wartość stałych uniwersalnych, takich jak Pi, z dowolną precyzją, tak więc jedyną przeszkodą w sprawdzeniu zgodności stron jest czas obliczeń.

Przed wprowadzeniem algorytmów takich jak ten matematycy musieli użyć istniejącej wiedzy matematycznej i twierdzeń, aby wysunąć takie przypuszczenie. Dzięki automatycznym przypuszczeniom generowanym przez algorytmy matematycy mogą wykorzystać je do odtworzenia ukrytych twierdzeń lub bardziej "eleganckich" wyników.

Najbardziej godnym uwagi odkryciem badaczy jest nie tyle nowa wiedza, ale nowe przypuszczenie o zaskakującym znaczeniu. Pozwala ono na obliczenie stałej Catalana, stałej uniwersalnej, której wartość jest potrzebna w wielu problemach matematycznych. Wyrażanie jej za pomocą ułamka ciągłego w nowo odkrytym przypuszczeniu pozwala na najszybsze jak dotąd jej obliczenie, pokonując wcześniejsze formuły, które wymagały więcej czasu na przetworzenie komputerowe. Wydaje się to oznaczać nowy punkt postępu dla informatyki, porównywany przez badaczy do momentu, gdy po raz pierwszy komputery pokonały szachistów.

Z czym AI nie daje rady

Algorytmy maszynowe z jednymi rzeczami, jak widać, radzą sobie w nowatorski i skuteczny sposób. Wobec innych problemów są bezradne. Zespół naukowców z Uniwersytetu Waterloo w Kanadzie odkrył klasę problemów, których nie może rozwiązać sztuczna inteligencja za pomocą uczenia maszynowego. Odkrycie ma związek z paradoksem opisanym w połowie ubiegłego wieku przez austriackiego matematyka Kurta Gödla.

Matematyk Shai Ben-David wraz ze swoim zespołem przedstawił w publikacji w "Nature" model nauczania maszynowego, zwany przewidywaniem maksimum (EMX). Z pozoru proste zadanie okazało się niewykonalne dla sztucznej inteligencji. Problem postawiony przez zespół Shai Ben-Davida sprowadza się do przewidzenia najbardziej korzystnej kampanii reklamowej skierowanej do najczęściej odwiedzających stronę czytelników. Liczba możliwości jest tak duża, że sieć neuronowa nie jest w stanie znaleźć funkcji, która będzie prawidłowo przewidywała zachowania użytkowników serwisu, mając do dyspozycji jedynie niewielką próbkę danych.

Okazało się, że niektóre problemy stawiane przed sieciami neuronowymi są równoważne hipotezie continuum postawionej przez Georga Cantora. Niemiecki matematyk udowodnił, że moc zbioru liczb naturalnych jest mniejsza niż moc zbioru liczb rzeczywistych. Następnie postawił pytanie, na które nie potrafił udzielić odpowiedzi. Mianowicie zastanawiał się, czy istnieje nieskończony zbiór, którego moc jest mniejsza od mocy zbioru liczb rzeczywistych, ale większa od mocy zbioru liczb naturalnych.

W XX wieku austriacki matematyk Kurt Gödel udowodnił, że hipoteza continuum jest nierozstrzygalna w obowiązującym systemie matematycznym. Teraz okazuje się, że na podobny problem nadziali się matematycy projektujący sieci neuronowe.

Zatem choć AI potrafi odnajdować formuły matematyczne dla nas niedostrzegalne, to jak widać, jest bezradna wobec fundamentalnych ograniczeń. Uczeni zastanawiają się, czy z problemami tej klasy, jak np. zbiory nieskończone, poradzą sobie komputery kwantowe.

Mirosław Usidus