Wybory a matematyka, czyli divide et impera

Łacińska sentencja użyta w tytule artykułu znaczy "dziel i rządź". Stosowano ją od zawsze. Wywołaj kłótnię w narodzie - a łatwiej go podbijesz. Hiszpańscy konkwistadorzy XVI i XVII wieku umiejętnie podburzali jedne plemiona Indian przeciw drugim. Bardzo wiele osiągnął w końcu XVIII wieku ambasador rosyjski Repnin: udało mu się wywołać ferment w ostatnich latach niepodległej Polski. Anglicy w swoim niegdysiejszym imperium robili to samo, a wojna w Jugosławii w 1990 r. zaczęła się od podburzenia Serbów przeciwko Chorwatom i na odwrót.
Przykłady celowego wywoływania konfliktów wewnątrz jednego kraju znamy. Na szczęście w obecnej Polsce nic takiego nie ma miejsca. Rządząca partia jest wzorem łagodności, umiaru i rozsądku, pełna szacunku dla opozycji, szanująca prawo, Konstytucję i wolę pewnego prostego, małego człowieka. Wygrywamy na forum międzynarodowym, często do zera (pamiętne zwycięstwo 27:0). Powodzi nam się i w sporcie: pamiętamy dramatyczny mecz hokeja na lodzie z Kamerunem. Nie ma żadnych afer, a politycy są kryształowi. Gdzie im tam w głowie własna kieszeń! Przewodzi partia. Pomożemy!
Stop, stop. Nie jesteśmy magazynem publicystycznym. Zobaczmy, jak można naginać proces decyzyjny w majestacie matematyki i… logiki. Pełny opis byłby dużą pracą, raczej publicystyczną niż naukową.
Są następujące możliwości.
Po pierwsze, manipulacja podziałem kraju na okręgi wyborcze.
Po drugie, wybór sposobu przeliczania głosów na mandaty poselskie lub (np. w przypadku wyborów prezydenckich w USA) na elektorskie.
Po trzecie: interpretacja, kiedy głos jest ważny, a kiedy nie.
Nie wymieniam tu jawnych nadużyć, jak manipulacja niewiedzą głosujących (za PRL wrzucenie pustego głosu oznaczało głosowanie na kandydatów wymienionych na początku listy), oszustwa przy liczeniu głosów i przesyłaniu danych wyżej.
Zacznę od gerrymanderingu. Co to za dziwny termin? Wyjaśniam nieco okrężną drogą.
Zdobyć punkty istotne
Czytelnicy zapewne znają punktację w tenisie. Zdobywamy punkty, gemy i sety. Do wygrania gema potrzebne jest wygranie co najmniej czterech piłek (punktów), ale o co najmniej dwie więcej niż przeciwnik. Wyjątek stanowi gem w tie-breaku - gra się w nim do siedmiu wygranych punktów (piłek), też z zachowaniem zasady przewagi dwóch piłek. Wygrane piłki numeruje się dziwnie: 15, 30, 40, potem używamy tylko terminów "przewaga - równowaga".
Gemy zbierane są w sety. Do wygrania seta trzeba mieć co najmniej sześć gemów i o co najmniej dwa więcej niż przeciwnik. Przy stanie 6:6 na ogół rozgrywany jest tie-break. Mecze rozgrywane są albo do dwóch, albo do trzech wygranych setów. "Do dwóch wygranych" znaczy, że wygrywa ten, kto wygra dwa sety. Wynik może być zatem 2:0 albo 2:1 (no i symetrycznie 0:2, 1:2). Ten regulamin sprawia, że aby wygrać mecz, nie trzeba wygrać więcej piłek (punktów). Mówiąc w dużym uproszczeniu, trzeba wygrywać te ważniejsze. Ekstremalny przykład to taki, gdzie tenisista A wygrywa pierwszy set 6:0, a dwa pozostałe przegrywa po 4:6. Przegrywa mecz, mimo że wygrał 14 gemów, a przeciwnik 12.
Zwrócę uwagę na to, co napisałem przed chwilą. W tenisie są punkty ważniejsze i mniej ważne. Dobry tenisista koncentruje się na tych najważniejszych.
Los milionów w łapkach salamandry
Przechodzimy do wyborów politycznych. Ogólniej, do wyborów, gdzie decydują tysiące czy miliony.
Trzeba najpierw podzielić kraj na okręgi wyborcze. Jak? Wszystko jedno, jak? O, nie! Pierwszym, który wpadł na pomysł, jak to zrobić, by zwiększyć szanse własnej partii, był Elbridge Gerry, polityk amerykański sprzed dwustu lat. Jeden z zaproponowanych przez niego okręgów miał kształt… salamandry i z połączenia jego nazwiska z tym płazem ogoniastym powstał termin gerrymandering. Działa dość dobrze przy jednomandatowych okręgach, a więc nie ma bezpośredniego zastosowania do Polski. Przy wielomandatowych jest… bardzo różnie. Niekiedy można się sparzyć. A rzecz jest ciekawa.
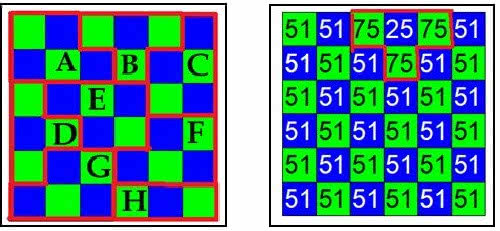
Wyobraźmy sobie zatem pewien kraj, gęsto zaludniony i o bardzo regularnych granicach: idealny kwadrat, a w nim małe pola-miasta. Lepszą analogią jest miasto i wybory burmistrza, ale matematycznie to bez różnicy. Rządząca partia niebieskich ma poparcie w sektorach zaznaczonych na niebiesko na rys. 1. Zieloni prowadzą w kwadratach zielonych. Ponieważ mówimy o okręgach jednomandatowych, więc nie jest istotne, jaka jest przewaga. W skali kraju mamy remis, tyle samo kwadracików jest niebieskich, co zielonych. Ale rządzą niebiescy i to oni wyznaczają podział kraju na regiony. Jest osiem okręgów wyborczych (1). Jakie są wyniki głosowania? Niespodziewane! Niebiescy wygrywają w A, C, E, F, G, a zatem w pięciu z ośmiu okręgów. Przy okręgach jednomandatowych mają przewagę 5:3 w skali kraju (ewentualnie miasta, jeżeli to wybory burmistrza).
Gerrymandering ma ważną zaletę z punktu widzenia partii, w której afery są na porządku dziennym. Wyobraźmy sobie, że w okręgu wyborczym B odkryto aferę – burmistrz defraudował pieniądze publiczne i jeszcze mówił, że to nic nie szkodzi. Sporo wyborców odwróciło się od niego. O ile przedtem głosy rozkładały się prawie po równo (51:49 na korzyść tej albo tej drugiej partii, to teraz w okręgu B w każdym małym obwodzie zieloni otrzymali po 75%, a niebiescy tylko 25. W skali kraju wcale to im jednak nie zaszkodziło (tabela 1). Stosując analogię tenisową, można powiedzieć, że tylko przegrali nieważny punkt.
| Okręg wyborczy | Niebiescy | Zieloni | Kto wygrywa |
| A | 251 | 249 | Niebiescy |
| B | 100 | 300 | Zieloni |
| C | 251 | 249 | Niebiescy |
| D | 198 | 202 | Zieloni |
| E | 251 | 249 | Niebiescy |
| F | 251 | 249 | Niebiescy |
| G | 251 | 249 | Niebiescy |
| H | 149 | 151 | Zieloni |
| Suma głosów | 1702 | 1898 | 5 do 3 dla Niebieskich |
Tabela 1. Liczba głosów 1898:1702 na korzyść Zielonych, ale mandaty poselskie 5:3 dla Niebieskich! W amerykańskich wyborach prezydenckich zdarza się, że wygrywający dostaje mniej głosów.
System jednomandatowy ma zalety i wady. Wziął się z angielskiej tradycji parlamentarnej. Aby choć trochę ukrócić zasadę "zwycięzca bierze wszystko", proponowano bardzo różne formuły matematyczne. Najbardziej powszechna była zasada "największej części ułamkowej". Załóżmy, że w okręgu Grodzisko Nadmorskie startują cztery partie A, B, C i D. Do zdobycia jest siedem mandatów. W wyborach partie te otrzymały odpowiednio 9934, 5765, 4031 i 1999 głosów; łącznie 21 729. Obliczamy:
7∙9934/21729=3,20
7∙5765/21729=1,86
7 ∙4031/21729=1,30
7∙1999/21729=0,64
To jasne; gdyby Rzeczpospolita była, jak mówi książę Radziwiłł w "Potopie", postawem czerwonego sukna, to partie rozdarłyby ją w proporcjach 320:186:130:64. Ale jest tylko siedem miejsc do podziału. Partii A należą się na pewno trzy miejsca (bo iloraz jest powyżej 3), partiom B, C - po jednym. Jak przydzielić pozostałe dwa? Narzuca się następujące rozwiązanie: dać tym partiom, którym "najmniej brakuje do pełnego głosu", czyli tym, które mają największą część ułamkową. Przypadają one zatem partiom B, D. Wynik przedstawmy zrozumiałym wykresem na rys. 3.
Co da jednak tzw. reguła d’Hondta? Omawiam ją trochę dalej. Polecam jako ćwiczenie. Wynik jest na rys. 4.
Polecam Czytelnikom jako następne łatwe ćwiczenie coś takiego: wyobraźmy sobie, że partie B, C i D zawierają porozumienie i idą do wyborów jako jeden blok - nazwijmy go E. Wówczas, jak wynika z reguły d’Hondta, odbierają jeden mandat partii A, czyli wynik A:E wynosi 3:4. Wniosek znany jest od lat jako przysłowie: Zgoda buduje, niezgoda rujnuje.
Całe szczęście, że przykłady, które tu podaję, są fikcyjne i wszelkie podobieństwo do znanych państw jest dziełem przypadku.
D’Hondt
Jak działa wspomniana metoda d’Hondta? Najlepiej wyjaśni to przykład. Załóżmy, że w pewnym okręgu w wyborach do Parlamentu Kłapadocji głosowano tak, jak pokazuje tabela 2.
| Nazwa partii | Głosów, N | N/2 | N/3 | N/4 | N/5 |
| Partia Totalnego Dobrobytu | 10 000 | 5000 | 3333 | 2500 | 2000 |
| Stronnictwo Obfitości | 6600 | 3300 | 2200 | 1650 | 1320 |
| Lokomotywa Postępu | 4800 | 2400 | 1600 | 1200 | 960 |
| Oszuści i Hochsztaplerzy | 3600 | 1800 | 1200 | 900 | 720 |
Tabela 2. Wynik głosowania w okręgu Kłapućko Małe w wyborach w Kłapadocji.
Okazało się, że partia Oszuści i Hochsztaplerzy wypadła tak dobrze tylko w Kłapućkach Małych. Globalnie nie uzyskali 5%, więc ich wyniki się nie liczą. Pozostałe liczby ustawiamy po kolei, nie zapominając, od jakiej partii pochodzą:
10 000 (PTD), 6600 (SO), 5000 (PTD), 4800 (LP), 3333 (PTD), 3300 (SO), 2500 (PTD), 2400 (LP), 2200 (SO) itd. W tej kolejności przydzielamy mandaty. Wynik bardzo zależy od tego, ile mandatów jest do zdobycia.
| 3 mandaty | PTD 2, SO 1, LP 0 |
| 4 mandaty | PTD 2, SO 1, LP 1 |
| 5 mandatów | PTD 3, SO 1, LP 1 |
| 6 mandatów | PTD 3, SO 2, LP 1 |
| 7 mandatów | PTD 4, SO 2, LP 1 |
| 8 mandatów | PTD 4, SO 2, LP 2 |
| 9 mandatów | PTD 4, SO 3, LP 2 |
Tabela 3. Rozdział mandatów w zależności od ich liczby.
Mówi się, że taki system spłaszcza wyniki - ukróca ewentualną dominację jednej partii. Sprawa jest jednak bardziej skomplikowana. Wszystko zależy od konkretnych danych. Nie mam miejsca na dłuższą dyskusję, zwrócę tylko uwagę na dwie ciekawostki:
1. Gdyby Oszuści i Hochsztaplerzy osiągnęli ogólnokrajowy próg wyborczy, wyniki mogłyby być inne. Nie zmieniłyby się, gdyby do zdobycia były trzy lub cztery mandaty, ale gdyby z okręgu wchodziło do parlamentu pięć osób, wynik wyglądałby tak: PTD 2, SO 1, LP 1, OiH 1. Partia PTD straciłaby bezwzględną większość. Działa to i w drugą stronę: jeżeli z jakieś partii wyłamie się małą frakcja, tracą wszyscy, łącznie z odszczepieńcami.
2. Gdyby SO i LP dogadali się i poszli do wyborów razem, przy żadnym układzie nie byłoby im gorzej, a zwykle lepiej.
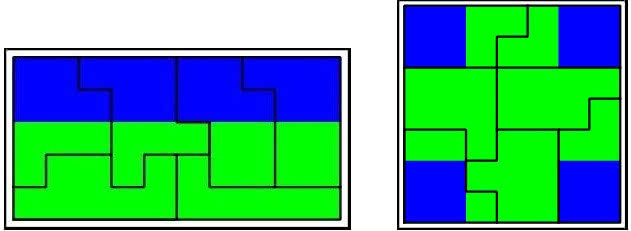
Zobaczmy jeszcze, jak potraktuje metoda d’Hondta sytuację z rys. 2, gdy w okręgu są do zdobycia dwa albo trzy mandaty. Przypominam, że taki gerrymandering w przypadku okręgów jednomandatowych dawał silne zwycięstwo Niebieskim. Przy dwumandatowych następuje totalna porażka, ale przy trzymandatowych znów gerrymandering wygrywa.
| Okręg wyborczy | Niebiescy | Zieloni | Metoda d’Hondta |
| A | 251 | 249 | Ilorazy: 251/249; rozkład 1-1 |
| B | 100 | 300 | 300/100; 0-2 |
| C | 251 | 249 | 251/249; 1-1 |
| D | 198 | 202 | 202/198; 1-1 |
| E | 251 | 249 | 251/249; 1-1 |
| F | 251 | 249 | 251/249; 1-1 |
| G | 251 | 249 | 251/249; 1-1 |
| H | 149 | 151 | 151/149; 1-1 |
| Suma głosów | 1702 | 1898 | Niebiescy 7 – Zieloni 9 |
Tabela 4. Sytuacja z rys. 2, ale przy dwumandatowych okręgach wyborczych. Porażka Niebieskich 7:9.
| Okręg wyborczy | Niebiescy | Zieloni | Metoda d’Hondta |
| A | 251 | 249 | Ilorazy: 251/249/125,5; rozkład 2-1 |
| B | 100 | 300 | 300/150/100; 0,5-2,5 |
| C | 251 | 249 | 251/249/125,5; 2-1 |
| D | 198 | 202 | 202/198/101; 1-2 |
| E | 251 | 249 | 251/249/125,5; 2-1 |
| F | 251 | 249 | 251/249/125,5; 2-1 |
| G | 251 | 249 | 251/249/125,5; 2-1 |
| H | 149 | 151 | 151/149/75,5; 1-2 |
| Suma głosów | 1702 | 1898 | Niebiescy 12,5 – Zieloni 11,5 |
Tabela 5. Sytuacja z rys. 2, ale przy trójmandatowych okręgach wyborczych.
Do pewnych osobliwości zaliczam "geometrię" przy kwalifikowaniu głosów jako ważne czy nieważne. W wielu krajach znakiem aprobaty jest "ptaszek", czyli jakby litera v, albo niekiedy Y. U nas jest krzyżyk x, co kojarzy się raczej z przekreśleniem (a więc odrzuceniem). Ustawodawca chciał to sprecyzować i dał quasi matematyczną definicję - "dwie przecinające się linie", interpretując, że dwie linie przy literce v nie są przecinające się.
Po pierwsze, w matematyce "przecinające się", znaczą "mające punkt wspólny" - szczególnie tak powinno się kojarzyć osobom młodszym (poniżej pięćdziesiątki), bo tak jest teraz w szkole. Jeżeli jednak ktoś nie wierzy w matematykę, może przypomnieć sobie, że na szosie rozjazd jest też skrzyżowaniem.
Lepiej już zostawić nieprecyzyjną definicję: każdy znak, który jednoznacznie wskazuje wybór kandydata na stanowisko, które kiedyś było zaszczytne, a teraz ma wyłącznie pejoratywne skojarzenie.