Matematyka prostych kresek
Temat szkoły brzmiał: "Hipotezy i problemy otwarte". Spotykam się niekiedy z poglądem, że w matematyce przecież już wszystko od dawna wiadomo. Nawet absolwenci politechniki często mówią, że "matematykę przerobiliśmy prawie całą". Nic bardziej mylnego - matematyka, jak zresztą każda nauka, jest w nieustannym, ciągłym rozwoju.
Odkrycia matematyczne mogą dotyczyć bardzo podstawowych praw. Kilkanaście lat temu forma Hewlett-Packard opublikowała algorytm mnożenia, stosowany w ich kalkulatorach. Nie łudźmy się: opublikowali, bo znaleźli lepszy, szybszy. Podobnie jest ze schematem rozwiązywania zwykłych, najprostszych równań - umiemy je rozwiązywać coraz szybciej. My - to znaczy nasze komputery, które bez nas nic by same nie zrobiły.
Rzeczy proste są w ogóle ciekawe. Mówił już o tym Pitagoras: piękne jest to, co opisuje się prostymi liczbami. Z tej zasady powstała cała teoria muzyki, harmonia - podstawa całej muzyki europejskiej. I w geometrii co proste, to ciekawe.
Pomówimy zatem o figurach, które są proste, a będzie to oznaczało nie tylko "nieskomplikowane", ale i że są złożone z fragmentów linii prostych, czyli odcinków. Dla pełności powinienem dodać: "są lub mogą być" (złożone z odcinków).
Z punktu widzenia pewnej geometrii łuk nie różni się od odcinka. Podróżując po łuku możemy nie zauważyć jego zakrzywienia. A wyobraź sobie, Czytelniku (będzie do mężczyzn), że czekając na ukochaną, chodzisz po uliczkach: z Kwiatowej skręcasz w prawo w Podleśną, potem znów w prawo w Czeremchową i jeszcze raz w prawo w Poziomkową. Dochodzisz do Kwiatowej i znów: Podleśna, Czeremchowa, Poziomkowa… Prawda, że "chodzisz w kółko"? - choć po kwadracie. Czytelniczki proszone są o wymyślenie podobnego przykładu, w którym same 'chodzą w kółko".
Ale do rzeczy, czyli do matematyki. Mamy w geometrii (zarówno elementarnej, jak i bardzo ogólnej) ciekawe pojęcie charakterystyki Eulera. Można ją znaleźć w prostych figurach, o jakich będzie tutaj, ale też i w wielościanach, w niemiłosiernie powykrzywianych przestrzeniach, w pękach wektorów i w algebrze abstrakcyjnej. Zwykle chodzi o naprzemienną sumę składników. Taka suma nie jest właściwie sumą, tylko… ale prosty przykład wyjaśni to najlepiej. Otóż 1+2+3+4+5+6 to suma, natomiast 1–2+3–4+5–6 to suma naprzemienna. Stawiamy na przemian plus i minus. Kilkanaście lat temu uczyliśmy (my, nauczyciele) o tym w szkole.
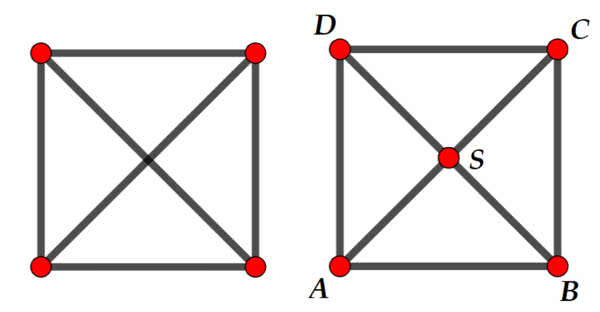
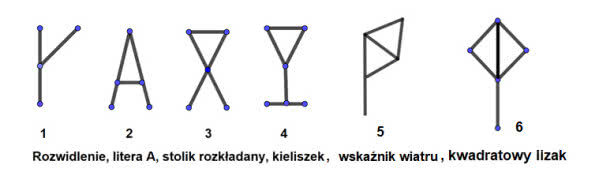
Nasze figury będą składać się tylko z odcinków, połączonych w węzłach (albo: wierzchołkach). Mogą to być trójkąty, dowolne wielokąty, linie łamane, rozgałęzione. Przyjmiemy tu umowę, że jeżeli dwa odcinki mają punkt wspólny, to jest on też wierzchołkiem (będę go nazywać też węzłem - rysunek 1).
A, B, C, D, S i osiem boków: AB, BC, CD, AD, AS, BS, CS, DS
Leonhard Euler był wybitnym matematykiem szwajcarskim, ale spędził wiele lat w Petersburgu, na dworze carycy Katarzyny - tej, która dość niechlubnie zapisała się w historii Polski. Napisał kilkaset prac matematycznych i jego nazwisko jest upamiętnione w kilkunastu nazwach różnych obiektów i pojęć matematycznych. Jednym z nich jest właśnie charakterystyka Eulera. Dla naszych figur, które są jak gdyby ułożone z patyczków, będzie to po prostu różnica liczby wierzchołków i liczby krawędzi, powiększona o 1, a zatem dla kwadratu z rysunku 1 otrzymamy 8–5+1=4. Zobaczmy kilka innych przykładów (rysunek 2).
Ujmę to wzorem. Oznaczę liczbę wierzchołków figury G przez e(G), a liczbę wierzchołków przez v(G). Oznaczenia te pochodzą z angielskiej terminologii: edge = krawędź, vertex = wierzchołek.
ch(G)=e(G)–v(G)+1
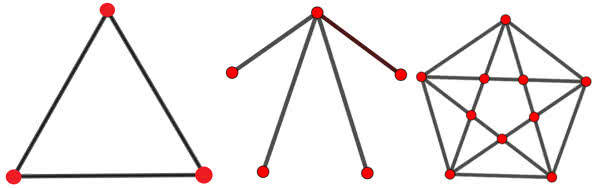
Obliczmy tę charakterystykę dla kilku grafów. Odcinek ma dwa końce (wierzchołki) i jedną krawędź, a więc charakterystykę 1. Trójkąt (rysunek 2) ma trzy wierzchołki i trzy krawędzie, a zatem charakterystykę 1. Każdy wielokąt ma też charakterystykę 1, bo ma tyle samo wierzchołków, co krawędzi. Graf w kształcie litery Y ma cztery wierzchołki i trzy krawędzie, czyli charakterystykę równą 0. "Ludzik" na rysunku 2 ma pięć wierzchołków i cztery krawędzie, a więc też charakterystykę 0.
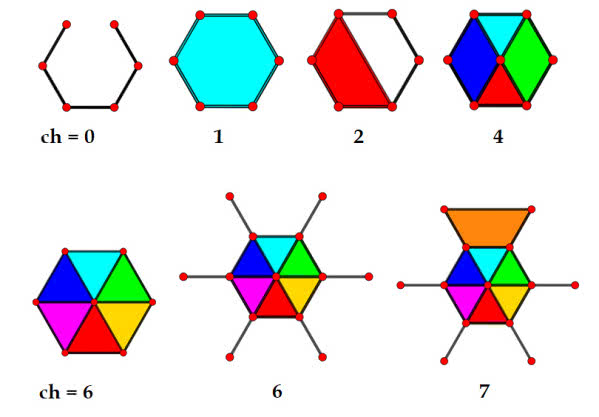
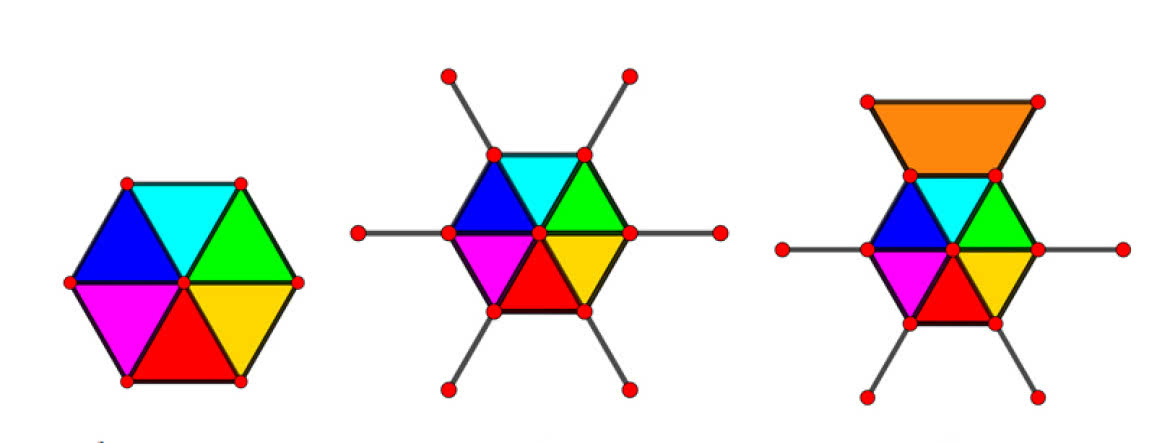
W pięciokącie z przekątnymi widzimy aż dziesięć wierzchołków, a łączy je dwadzieścia odcinków, co daje charakterystykę 20–10+1=11. Sześciokąt bez przekątnych ma charakterystykę 1. Wzrośnie ona, gdy będziemy dołączać przekątne. Dla piątego sześciokąta z rysunku 3 mamy: e(H)=12, v(H)=7. Zgadza się, ch(H)=12–7+1=6, a widzimy, że sześciokątna pizza została podzielona na sześć kawałków. Gdy do sześciokąta dołączymy wystające "szprychy", charakterystyka się nie zmieni, bo przybyło sześć wierzchołków i tyle samo krawędzi. Gdybyśmy jednak połączyli dwa nowe końce (charakterystyka wzrosłaby o 1, bo przy tej samej liczbie wierzchołków przybyłaby jedna krawędź. Inaczej rzecz ujmując, utworzyłby się jeden nowy obszar.
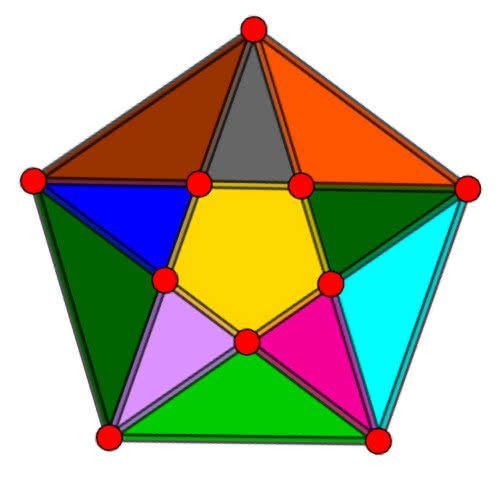
Analizując te przykłady, możemy się domyślić ogólnej zasady. Charakterystyka Eulera to liczba obszarów, które ogranicza nasza figura. Figury "cienkie", takie jak odcinek, litery Y, C, S, U, W, T, Z nie ograniczają nic (charakterystyka = zero). Każdy wielokąt ogranicza jeden obszar, kwadrat z przekątnymi cztery, a pięciokąt z przekątnymi (tak zwany pięciokąt gwiaździsty, pentagram - rysunek 4) - jedenaście.
Wyodrębnijmy w naszych figurach (jak gdyby ułożonych z patyczków) punkty końcowe. Łatwo pojąć, o co chodzi - to tak, jak z koleją w Zakopanem. Pociąg podjeżdża niemal pod sam Giewont i dalszej drogi nie ma. Odcinek (jak kij) ma dwa końce, podobnie figury w kształcie liter A, Y, C, P, R i kilku innych. Zamknięty trójkąt, kwadrat i wszystkie wielokąty nie mają punktów końcowych (matematyk powie: mają zero takich punktów), a sześciokąt ze szprychami (przedostatni na rysunku 3) ma ich sześć.
Niektóre figury są bardziej solidnie zbudowane niż inne. Gdy z wnętrza odcinka usuniemy choćby jeden punkt, odcinek się rozpadnie. Można to porównać do pęknięcia szyny na odcinku między stacjami A,B. Jeżeli jest to jedyna linia łącząca dwa duże obszary przemysłowe, to komunikacja między tymi obszarami staje się niemożliwa. Jeżeli jest to łącze jakiejś sieci (powiedzmy komputerowej), skutki są poważne. Zauważmy, że awaria na jednym z końców linii A, B nie daje takich skutków. Odcinek się nie rozpada, a pociągi może i nie wjadą na samą stację końcową, ale mogą się zatrzymać tuż przed nią - połączenie nie przerwało się. Było tak kiedyś na podwarszawskiej kolejce dojazdowej WKD. Pociąg nie mógł wjechać na końcową stację Grodzisk Radońska, ale zawracał na przystanku Nadarzyńska, odległym o 200 metrów. Połączenie z Warszawą nie przerwało się.
Inaczej jest dla trójkąta i ogólnie każdego zamkniętego wielokąta. Żeby rozpadł się na dwa kawałki, trzeba go przerwać w dwóch punktach. Wszystko jedno, w których dwóch (albo trzech czy więcej - chodzi nam tylko, czy połączenie zostanie przerwane, czy nie). Dla kwadratu z jedną przekątną rozerwanie w dwóch punktach może nie wystarczyć (na przykład usunięcie dwóch narożników przez które nie przechodzi przekątna).
Dochodzimy do głównego tematu artykułu. Nazwę liczbą przetrwania taką największą liczbę n, że figura może "przetrwać" - to znaczy nie rozpaść się na części - nawet po usunięciu z niej n punktów. Określenie może trochę skomplikowane, ale przykłady rozjaśnią, co chodzi. Zacznijmy od początku, czyli od liczby przetrwania 1. Każdy wielokąt ma liczbę przetrwania 1. Jeden punkt z obwodu można usunąć, ale usunięcie każdych dwóch ma już "poważne konsekwencje" - wielokąt rozpadnie się. Dla odcinka ta liczba jest równa 2 - bo możemy usunąć dwa końce i odcinek pozostanie odcinkiem. Wprawdzie bez końców, ale co to szkodzi? Natomiast każde usunięcie trzech punktów już - jak to mówią matematycy - rozspójnia odcinek. Nie jest to już figura spójna - ma dwie albo więcej oddzielnych części.
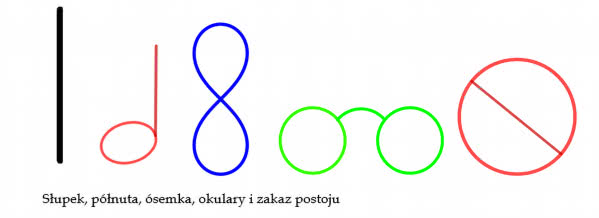
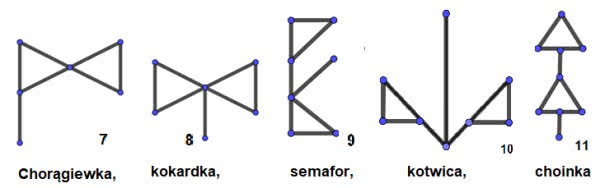
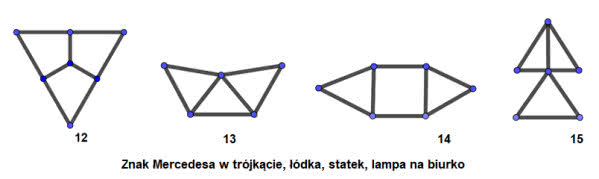
Spójrzmy na rysunek 5. Są na nim wszystkie figury o liczbie przetrwania 2. Zaraz, zaraz, ale miały być złożone z odcinków! Niezupełnie, przecież napisałem wyżej, że "są, lub mogą być". Co to znaczy? To, że mogę na przykład "ósemkę" zamienić na dwa trójkąty stykające się wierzchołkami, a "okulary" przez trójkąty połączone poprzeczką. Własności figur, które tu badamy, nie zmienią się. To ważna zasada matematyczna - znajdowanie figur, które mają te same własności, a są prostsze. Znak półnuty jest równoważny ze znakiem drogowym "ustąp pierwszeństwa przejazdu" (rysunek 6). Ósemka to dwa trójkąty złączone dzióbkami, a okulary to trójkąty połączone poprzeczką.
Nie bardzo trudno znaleźć wszystkie figury o liczbie przetrwania 3. To jak nieco skomplikowane SUDOKU - wystarczy mieć trochę spokoju, trochę cierpliwości i pomyśleć. Może jeszcze jedno: być wyczulonym na to, jakie figury są "takie same", a jakie nie. Dlaczego dwa trójkąty stykające się wierzchołkami to z naszego punktu widzenia inna figura niż trójkąty stykające się bokami? Można to różnie tłumaczyć, ale może najprościej jest tak. Pierwsza z nich ma skrzyżowanie, w którym przecinają się dwie ulice (inaczej: schodzą się cztery uliczki). Druga zamiast takiego skrzyżowania ma dwa z trzema dochodzącymi uliczkami. To je rozróżnia.
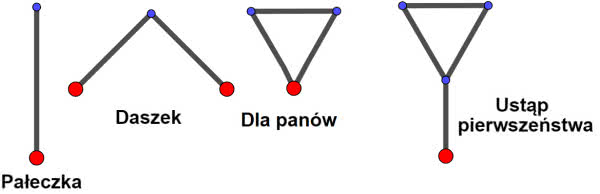
Po spędzeniu niezbyt długiego - chociaż i niezbyt krótkiego - czasu nad takimi łamigłówkami możemy odkryć, co dalej. Mianowicie, że każdy graf o liczbie przetrwania n powstaje z grafu o liczbie o jeden mniejszej (a zatem n–1) przez przyłączenie (w punktach zaznaczonych na czerwono) jednej z następujących czterech figur na rysunku 6.
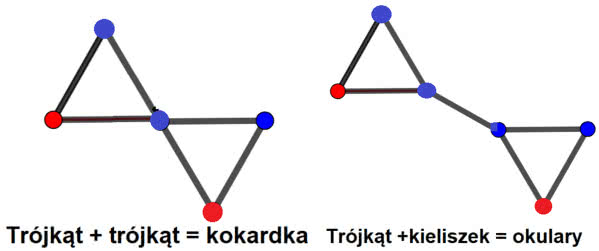
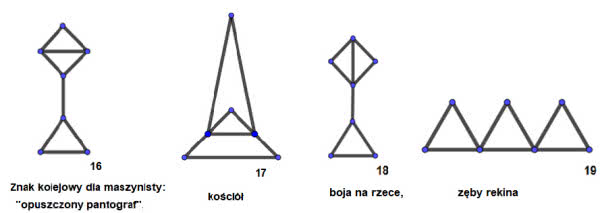
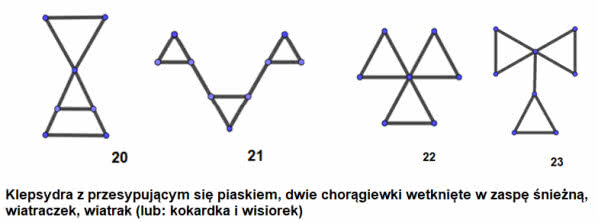
Zobaczmy to. Trójkąt ma liczbę przetrwania 1. Dołączając do niego pałeczkę, otrzymujemy znak drogowy "jesteśmy na drodze podporządkowanej". Złączenie trójkątów to kokardka, a dołączenie znaku podporządkowania do trójkąta daje okulary (rysunek 7). Na każdej z tych figur możemy usunąć punkty zaznaczone na czerwono i figura się nie rozpadnie.
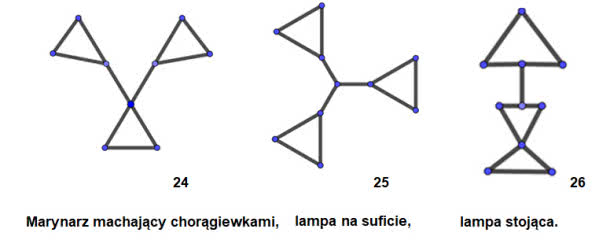
Możemy teraz "przysiąść fałdów" i narysować figury o liczbie przetrwania 3. Oto one. Jest ich 26. Dla osób oznajmionych z topologią: są to figury z dokładnością do równoważności topologicznej, czyli homeomorfizmu. Nazwy ich są mojego pomysłu.
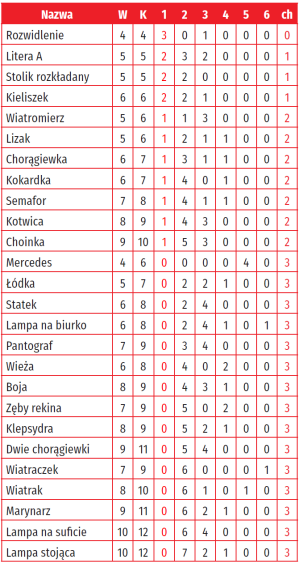
Ujmijmy to tabelką: W jej kolumnach mamy po kolei: W = liczba wierzchołków (węzłów), K - liczba kolumn, "1" - liczba końców (= punktów pojedynczych), "2" - liczba punktów krotności 2 (wychodzą z niego dwie drogi), "3", "4", "5", "6" liczba punktów o krotnościach 3,4,5,6, wreszcie "ch" to charakterystyka Eulera. Matematycznie rzecz biorąc, punkty rzędu 2 są nieistotne, ale miałem wiele radości, znajdując figury, które coś przypominają, jakieś ciekawe kształty.
Zadanie (nie bardzo trudne): jak obliczyć K, mając W oraz kolumny "1" do "6"?
Tabelka jest poniżej. Postaram się odpowiedzieć na pytanie: czy to jest tylko igraszka matematyków, czy może to ma jakieś zastosowania. Otóż jedno i drugie. Są tematy, które interesują matematyków same z siebie. "Jak to jest?". Czy jakieś równanie ma rozwiązanie, czy dana konstrukcja jest możliwa, jak ułożone są liczby na osi, jakie własności mają konfiguracje linii prostych, jakie stosunki przestrzenne panują w wielościanach, jakie własności mają sieci połączeń i tak dalej. To matematycy robią z czystej ciekawości: zaglądamy do naszego świata matematycznego. Ale teraz pomyślmy o tym ostatnim temacie, który wymieniłem: sieci. Możemy nimi przesyłać informacje i wagony kolejowe, transportować narciarzy, przesyłać prąd, wodę, jeździć samochodami. Sieci są wszędzie. Jak bezpieczna jest nasza sieć? Jakie zakłócenia będą katastrofalne, a jakie nie zakłócą jej działania? Jak spadnie przepustowość, gdy ulegnie dającej się ominąć awarii? W tym jest nie jeden, a kilka działów matematyki, ale o tym innym razem.
Jak pisałem, to wszystko da się zrobić bez użycia metod komputerowych. Dla wyższych liczb przetrwania to już nam się nie uda. Dla n=4 jest tych figur 213; być może benedyktyńską pracą dałoby się dojść i do tego wyniku. Następnie, dla n=5 jest tych figur 2310, dla n=6 aż 32512 i chyba nie wiadomo, co dla n=7 i wyższych.
Na zakończenie krótka historia odkrycia twierdzeń, o których pisałem… i smutna refleksja. W 1996 roku N.M. Copper napisał artykuł o liczbach przetrwania (tak naprawdę to o liczbach rozcinania, różnica jest mało znacząca). Przyznawał, że wiele jego odkryć pochodziło z badań Helmy Gladiness i Marcela van der Vela. Tej dwójce autorów najwyraźniej "nie chciało się" spisywać swoich wyników (tak bywa, choć rzadko!) i zrobili to dopiero w 2011 roku. Jest to właśnie rzecz dzisiaj nietypowa: znaczna większość naukowców staje na głowie, by opublikować swoje wyniki, gdy "są jeszcze ciepłe", bo a nuż uprzedzi ich konkurencja. Pozornie jest o co się bić: stypendia, granty, zasługi, czyli w rezultacie pieniądze. Tak było zawsze z odkryciami i wynalazkami. Dzisiaj to wszystko blednie. Zaczyna się liczyć co innego.