John Horton Conway, kosmologia i Stanisław Lem

John H. Conway (mylony niekiedy z równie znanym, rdzennie amerykańskim matematykiem, nazywającym się John Bligh Conway) był znany ze swojej oryginalnej, bardzo nietypowej i bardzo trudnej matematyki - ubranej w proste i dające się każdemu wytłumaczyć pojęcia i zasady. Można powiedzieć, że za pomocą klasycznej matematyki nie da się nawet ugryźć tych zagadnień - owszem, można je "polizać", coś obliczyć, ale na ogólne rozwiązanie szans nie ma. Nie ma nawet języka, w którym można by je wyrazić.

Napisałem, że wszystko da się wytłumaczyć. Oto dwa przykłady zagadnień Conwaya. Można powiedzieć, że dotyczą biologii i chemii. Dlaczego tylko "można powiedzieć"? No, bo tak. Najpierw o grze Life. Po skomputeryzowaniu straciła wiele uroku. Po co myśleć - włączę komputer i wszystko zobaczę. Ale nie narzekajmy. Na pomysł gry wpadł Conway z całkiem poważnych rozważań, czy maszyna może zbudować drugą taką samą albo nawet bardziej skomplikowaną. Przecież w świecie istot żywych ewolucja działa właśnie w tę stronę: kolejne potomne organizmy są coraz bardziej skomplikowane - choć zmiany następują bardzo powoli. Czy z maszynami jest tak samo, czy może to jest cecha charakterystyczna życia?

Najpierw więc o podstawach cybernetyki. Za jej pioniera uważany jest John von Neumann, (a właściwie János Lajos Neumann, 1903-1957) - węgierski matematyk, pracujący od 1937 roku w USA). Wytłumaczył on, jak maszyna może zbudować taką samą, a nawet bardziej złożoną i wobec tego maszyny mogą się też powielać (słowo "rozmnażać" brzmi bardzo biologicznie). Dzisiaj pomysł Neumanna wydaje się naturalny, ale tak bywa często z pionierskimi odkryciami.

Niech nasz automat składa się z trzech jednostek: konstruktora A, reproduktora B i kontrolera C. Mają oni takie oto zadania. Konstruktor potrafi zbudować każde urządzenie, jeżeli tylko ma instrukcję F, jak to zrobić. Zakładamy oczywiście, że jest dostępny "magazyn części". Organizmy biologiczne też muszą się czymś żywić. Reproduktor potrafi tylko jedno: przekopiować instrukcję budowy F. Wreszcie kontroler - mózg samoreprodukującej się maszyny - dokonuje następujących czynności:

1. Włącza konstruktora, żeby zbudował automat x na podstawie posiadanego opisu F(x),
2. Włącza reproduktora, żeby skopiował F(x),
3. Wyposaża zbudowany automat w jego własny opis F(x),
4. Oddziela zespół x+F(x) od A+B+C.

1. Po lewej - położenie wyjściowe, w środku wyjaśnienie reguł: czerwone kropki znikają, pojawiają się niebieskie. Po prawej wynik

2. Dalsze trzy pokolenia. Po kilku następnych kolonia wchodzi w stan "2+2"; a co to znaczy, można się przekonać, wykonując kilka ruchów

3. Kot z "Alicji w Krainie Czarów". W szóstym pokoleniu zostają z niego tylko wąsy. W siódmym "koniczynka", czyli stan "2+2", już niezmienny

Spójrzmy teraz na zespół D=A+B+C, wyposażony w instrukcję własnej budowy. Z powyższego opisu wynika, że ma on zdolność samoreprodukcji. Napotykamy tu "te same" kłopoty, co w kosmologii i biologii: skąd to się wzięło, jaki był początek? Czy "coś" może powstać z "niczego"? To już jest filozofia, wiara i teologia, i nie będę o tym pisać.

Można jednak do problemu reprodukcji automatów podejść bardziej "biologicznie" i taki model stworzył właśnie Conway. Jest to oczywiście tylko prosta gra - ale wiele się z niej można nauczyć, a jest po prostu ciekawa, a dla piszącego te słowa była pierwszym napisanym programem komputerowym w zapomnianym już języku FORTRAN. Ale wtedy jeszcze dinozaury po świecie chodziły… A o tej grze było już kilka razy w naszym miesięczniku.

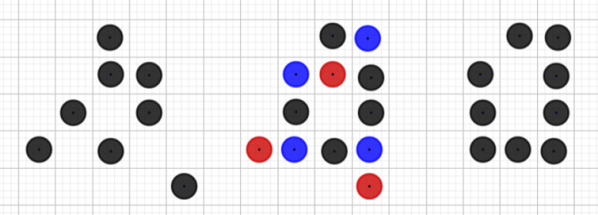
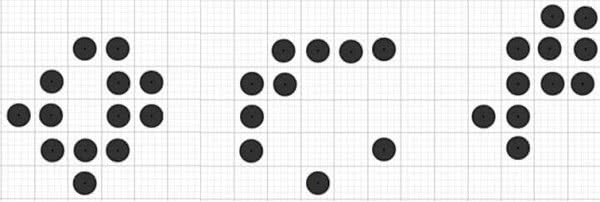
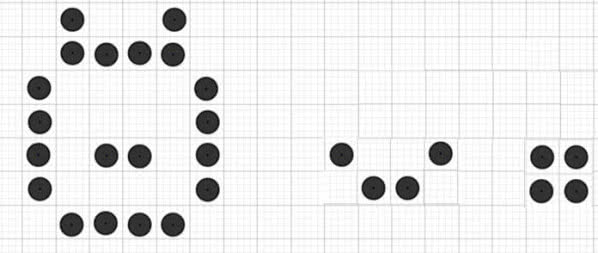
Otóż na pokratkowanej płaszczyźnie żyją sobie robaczki-automaty. Rodzą się, przeżywają i umierają według następujących reguł:

1. Robaczek, który nie sąsiaduje z żadnym, umiera z samotności,
2. Robaczek, który sąsiaduje z czterema lub więcej, umiera wskutek przeludnienia,
3. W tych (i tylko w tych) wolnych kratkach-komórkach płaszczyzny, które sąsiadują z trzema żyjącymi robaczkami, w następnym pokoleniu pojawia się nowy osobnik,
4. Urodzenia i zgony zachodzą w tej samej chwili, tak że rozwój populacji odbywa się skokowo. Kratka "sąsiednia" oznacza kratkę mającą wspólny bok albo tylko wierzchołek z daną. Każda kratka ma zatem ośmiu sąsiadów.

Można także tę grę uważać za model rozwoju kolonizacji jakieś planety. "Robaczki" to wioski osadników. Daleko idąca modyfikacja takiej gry daje wartościowy model rozwoju naszych miast i wiosek. Ale to już jest matematyka z naprawdę wysokiej półki. Z problemów czysto matematycznych, związanych z tą grą, wymienię jeden: poznać konfiguracje, które nie mają poprzedników; powstały jakby z niczego. Zostały stworzone. Jest ich niewiele, najmniejsze mają po 100 komórek.

Ta gra wzbudziła zainteresowanie automatami komórkowymi oraz, ogólniej, sposobami, w jaki przy zastosowaniu tylko kilku prostych reguł powstają skomplikowane struktury. Zajmują się tym nie tylko matematycy, ale i fizycy, biologowie i ekonomiści.

Tu dygresja "historyczna". Przytoczę swoje własne rady, jak grać w grę Conwaya. Rady owe pochodzą z książki, którą pisałem w 1983 roku - na kilka lat przed gwałtownym wejściem PC-tów do powszechnego użytku:

     0. Używamy pionków warcabowych, ale zwykła szachownica jest za mała i trzeba na papierze narysować    większą. Układamy wyjściową konfigurację z białych pionków.
     1. Na pionku, który nie przeżyje do następnego pokolenia, kładziemy drugi czarny pionek.
     2. Na każdym wolnym polu, sąsiadującym z trzema zajętymi, kładziemy biały pionek.
     3. Sprawdzamy starannie. Pomyłki są nieodwracalne, jak w prawdziwej ewolucji.
     4. Usuwamy wszystkie dwupionkowe stosiki. Zapisujemy nowo powstałą konfigurację na kartce. Jeśli nam się nie znudziło, idziemy do punktu nr 1 tej instrukcji. W przeciwnym razie kończymy grę.

Taaak. Jak pisałem, dziś łatwo znaleźć programy, generujące dziesiątki, a może i setki pokoleń na sekundę. Polecam - wszystko łatwo osiągalne w Internecie.

Bardziej niesamowity jest jeszcze inny pomysł Johna Conwaya. Bez wielkiej przesady mogę powiedzieć, że wywołuje we mnie "dreszcz metafizyczny", chociaż model jest sztuczny i może się nawet wydać niezbyt rozsądny. Ot, taka igraszka matematyków. Zobaczmy. Nazywa się to look-and-say, czyli zobacz-i-powiedz. Zaczynamy od dowolnej liczby, wystarczy jednocyfrowa. Najlepiej widać wszystko, gdy zaczniemy od trójki.

Piszemy: 3. Czytamy: j e d n a t r ó j k a. Zapisujemy tak, jak słyszeliśmy, jedna trójka, 13. Czytamy dalej: 13 to jedna jedynka, jedna trójka. Zapisujemy: 1113. 1113 to trzy jedynki, jedna trójka, czyli w zapisie: 
3113. 3113 to jedna trójka, dwie jedynki, jedna trójka, czyli 132113. Zapisałem to inną czcionką, za chwilę zobaczymy dlaczego. I jeszcze nazwę ten ciąg Ho, czyli symbolem pierwiastka chemicznego holm, z grupy lantanowców. Dlaczego? To jest właśnie "jądrem sedna" całej zabawy. Idziemy dalej: 132113 to przecież jedna jedynka, jedna trójka, jedna dwójka, dwie jedynki i jedna trójka. Tu mamy już dłuższy ciąg: 1113122113. Widzimy, że zaczyna się od na znane już 1113. Aby "poczuć bluesa", musimy jeszcze się potrudzić, choć cyferki na pewno skaczą nam w oczach.

1113122113 = trzy jedynki, jedna trójka, jedna jedynka, dwie dwójki, dwie jedynki, jedna trójka. Tłumaczymy to znów na cyfry: 311311222113. I może jeszcze raz: 311311222113 = jedna trójka, dwie jedynki, jedna trójka, dwie jedynki, trzy dwójki, dwie jedynki, jedna trójka. Następnym wyrazem ciągu jest wobec tego 13211321322113, czyli Ho+21322113.

No właśnie - teraz o chemii. Wszyscy powinni pamiętać, ile jest pierwiastków chemicznych, a w każdym razie, ile ich występuje naturalnie w przyrodzie. Dziewięćdziesiąt dwa. Pierwiastki o liczbach atomowych wyższych niż 92 określa się nazwą "transuranowce", czyli "położone za uranem". Wszystkie te pierwiastki zostały wytworzone przez człowieka w wywołanych sztucznie reakcjach jądrowych (dopiero później stwierdzono występowanie śladowych ilości neptunu i plutonu w rudach uranu).

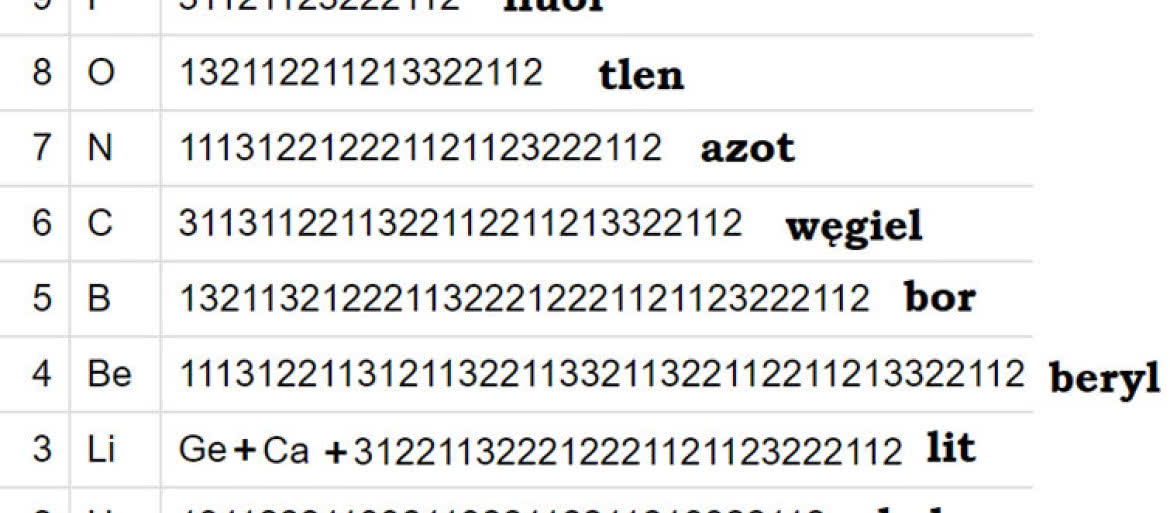
Tyle samo jest "pierwiastków Conwaya", to znaczy powtarzających się grup cyfr w naszej grze-zabawie zobacz-i-powiedz. Gdy będziemy kontynuować postępowanie bez końca, nie odkryjemy już niczego innego - wszystko będzie składać się z pierwszych dziewięćdziesięciu dwóch "pierwiastków". Stwórzmy tabelę, zaczynając od pierwiastka z największą liczbą atomową 92, a kończąc na wodorze. Każdy następny ciąg w kolumnie tabelki powstaje z poprzedniego przez look-and-say. Można stworzyć z tego i tablicę Mendelejewa: wpisanie do przeglądarki haseł look and say i Cosmological theorem zaprowadzi Czytelnika do dalszych rewelacji na ten temat, w tym zdumiewającej stałej Conwaya, będącej pierwiastkiem pewnego wielomianu 35 stopnia - zbyt skomplikowanym, żeby go tu wypisać. Wspomnę tylko jedno związane z tym zagadnienie matematyczne: w kolejnych wyrazach ciągu (o wyrazie startowym będącym liczbą jednocyfrową) występują tylko jedynki, dwójki i trójki, a poza tym żadna z cyfr nie powtarza się więcej niż trzykrotnie. To trudno udowodnić. Oto początek i koniec tabeli. W latach osiemdziesiątych zeszłego wieku modna była książka, której autorem był Hoimar von Ditfurth Na początku był wodór.

Ale zwrócę uwagę na jeszcze jeden szczegół. Jak wspomniałem, ciąg Conwaya można zacząć od dowolnej liczby. Spróbujmy z 2021. Jedna dwójka jedno zero jedna dwójka jedna jedynka, czyli 12101211. Czytajmy tę liczbę: jedna jedynka, jedna dwójka, jedna jedynka, jedno zero, jedna jedynka, jedna dwójka, dwie jedynki, czyli 11121110111221. I jeszcze dwa razy. Jak się bawić, to się bawić:

11121110111221 = trzy jedynki, jedna dwójka, trzy jedynki, jedno zero, trzy jedynki, dwie dwójki, jedna jedynka = 31123110312211.

31123110312211 = jedna trójka, dwie jedynki, jedna dwójka, jedna trójka, dwie jedynki, jedno zero, jedna trójka, jedna jedynka, dwie dwójki, dwie jedynki = 13211213211013112221.

Wszystko podobnie, tylko "plącze się" jedno zero i nigdy nie zniknie ani się nie rozmnoży. A ów "szczegół", na który chciałem zwrócić uwagę, to, co się dzieje, gdy weźmiemy jako liczbę początkową 22 (przypomnijmy sobie "Paragraf 22" jak i to, że to połowa 44 !): 22 = dwie dwójki = 22 = dwie dwójki= 22 = dwie dwójki = 22 = …

To jedyna liczba tego rodzaju. Początek i koniec. Dla wyjściowej 222 jest już zupełnie "normalnie":

222 = trzy dwójki = 32 = jedna jedynka, jedna dwójka = 1112 = trzy jedynki.

W klasyfikacji Conwaya 1112 jest to potas z liczbą atomową 19, a on przechodzi w arsen (3112), a ten w chlor 132112 o liczbie atomowej 17.

Zainteresowanych Czytelników odsyłam (wszystko w zasięgu kliknięcia) do artykułu Conwaya The weird and Wonderful Chemistry of Audioactive Decay, a swoistą tablicę Mendelejewa–Conwaya można znaleźć, wpisując w przeglądarce na przykład frazę Deux (deux?) minutes pour la suite de Conway.

Czy to ma jakiś sens, czy to tylko zabawa bez sensu i konsekwencji? Nie wiemy. Zbieżność danych matematycznych i chemicznych może szokować, ale bezpośredniego związku na pewno nie ma. Jest tylko ogólna refleksja nad zasadami budowy… naszego umysłu. A ponieważ jesteśmy cząstką Wszechświata, zatem i…

Nie dokończę myśli. Przypomnę, że rok 2021 został ogłoszony rokiem Stanisława Lema. W powieści "Głos Pana" opisuje on zmagania międzynarodowego zespołu, który ma odczytać tajemniczy komunikat, odebrany na Ziemi z głębin Kosmosu. Po przełożeniu na ciąg zer i jedynek wychodzi niezbicie, że jest to komunikat istot rozumnych, że ktoś nam chciał coś przekazać. Ale co? Tego nie udaje się odgadnąć. Lem wypowiada tam głęboką myśl, że jeżeli depesza zawiera jakąś treść, to da się ją wcześniej czy później wyłuskać. Ale czy taka treść istnieje? Może w odległej galaktyce jakieś dziecko zabawiało się klawiaturą?

Na szczęście jestem matematykiem i nie muszę aż tak głęboko przejmować się grą Johna Hortona Conwaya.

Michał Szurek

Zobacz także:

Kolorowa matematyka
Figury chiralne
Szyfry i szpiedzy