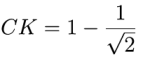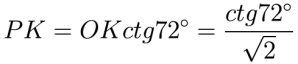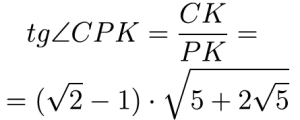Stara podłoga, urok ośmiokąta i Apolonia Inteligentna

Krytykowanie szkoły i nauczycieli jest dość modne i łatwe - każdy uważa, że się zna i każdy nagina model nauczania do swoich wyobrażeń. O politykach nie będę tu mówić, bo lekarz zabronił mi się denerwować, ale z przykrością wspomnę i o wielu profesorach, którzy uważają, że każda szkoła ma być taka sama: elitarna, ucząca nowocześnie, na najwyższym poziomie, przekazująca najlepsze wzorce i tak dalej. Trudno się z tym nie zgodzić, tak jak z hasłem, że wszyscy powinni być szczęśliwi, nie pracować ponad siły, dobrze zarabiać i w ogóle mieć zadowolenie z życia. Tylko jak to osiągnąć?

Dyskusja na forum publicznym ożywiła się kilka miesięcy temu, gdy nauczyliśmy się rozmawiać z Apolonią Inteligentną - tak na własny użytek nazywam AI, artificial intelligence, sztuczną inteligencję. O tym innym razem - po co sobie psuć nastrój?

Próbuję, z różnym skutkiem, realizować hasło, że uczymy nie tylko matematyki, ale i przez matematykę. Że matematyka jest wszędzie, że ważna jest nie tyle ona sama, co myślenie „typu matematycznego”. Trudno w kilu słowach opisać, co mam na myśli. Nie muszę teoretyzować i po prostu opiszę pewne swoje zajęcia; niestety - dla dzieci o możliwościach intelektualnych większych od przeciętnej. Piszę „niestety”, bo to nie oni mają największy wpływ na ogólny poziom wykształcenia społeczeństwa.

Jak co roku, w czerwcu brałem udział w obozie naukowym dla uczniów szkół podstawowych - stypendystów Krajowego Funduszu na rzecz Dzieci. Oczywiście nie jako podopieczny, ale wcale nie żałuję, że nie jestem dzieckiem. Natomiast, jak zwykle zaskakuje mnie zarówno wiedza, jak i otwartość umysłu stypendystów. Nie chodzi mi tylko o matematykę, ale o wszechstronne walory intelektualne tych dzieci. Owszem, nie są to typowi uczniowie naszej targanej trudnościami szkoły. Natomiast - co należy mocno podkreślić - zgodnie z polityką Funduszu, na obozie nie ma uczniów szkół o najlepszej renomie. Przeważają także dzieci z małych miasteczek i wsi. Zdolności intelektualne są w społeczeństwie rozrzucone sprawiedliwie, ale wciąż trudniej jest dzieciom z takich właśnie ośrodków. Fundusz chce wyrównywać szanse.

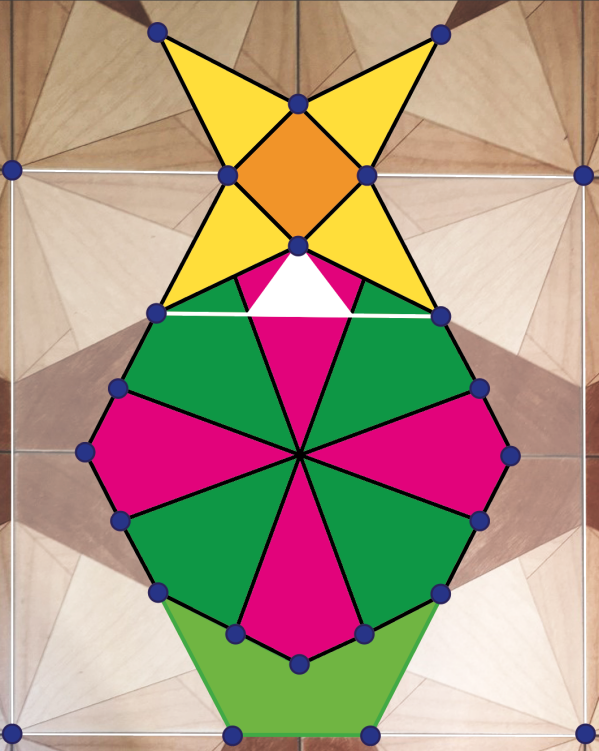
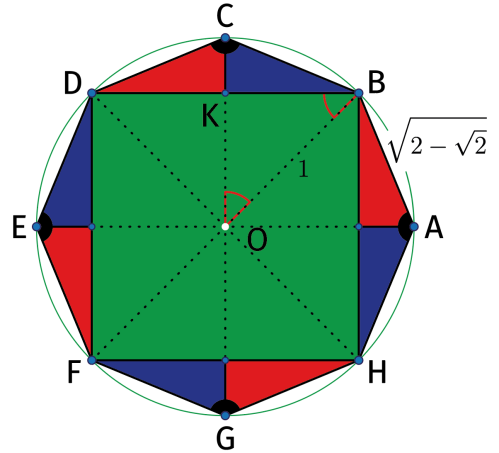
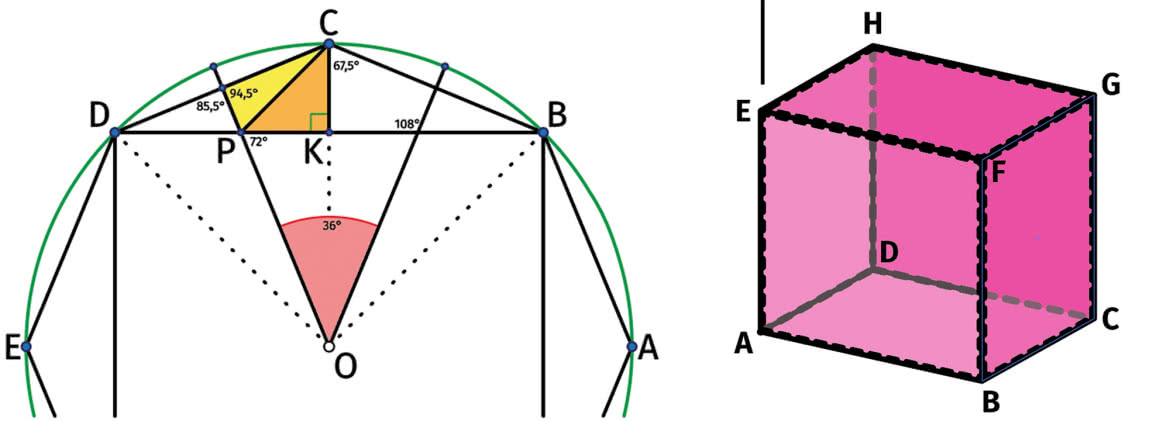
Ale to inny temat. Miałem oczywiście przygotowane tematy na trzydniowe zajęcia, ale po wejściu do ośrodka, w którym odbywał się obóz, natychmiast jeden z tych tematów zmieniłem. Zobaczyłem bowiem na podłodze taki oto ornament (1). Lubię prowadzić zajęcia na temat „matematyka wokół nas”. Zajęliśmy się zatem geometrią, ukrytą za tym ornamentem. Najpierw rzuciłem ogólne pytanie: co tu jest ciekawego? Jakie wielokąty widzicie?

Trochę zdziwiłem, że pierwsze, co zobaczyli, to duże kwadraty. Na pytanie: a gdzie są inne kwadraty, nie od razu odpowiedzieli. Właściwie to musiałem im pokazać - to te małe, wpisane w gwiazdy czteroramienne (pomarańczowe na rysunku 2).

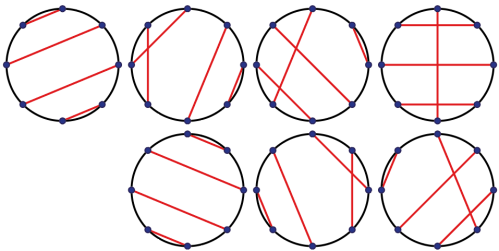
Moi uczniowie wiedzieli, że różowe i ciemnozielone czworokąty na rysunku 2 („latawce”) nazywają się w matematyce deltoidami. Nie zauważyli, że są one różnych rozmiarów, to znaczy, że mają (różowe i zielone) różne kąty. Różowe są nieco węższe. Potem dostrzegli ośmiokąty foremne. Wykorzystałem to do zadań o tej interesującej figurze - a zacząłem daleko od matematyki, od krótkiej dyskusji, jaki znak drogowy ma kształt ośmiokąta i dlaczego (3). To oczywiście każdy wiedział. Potem krótko porozmawialiśmy o systemie ósemkowym.

Zadanie 1

Przedstawić 2023 w systemie ósemkowym.

Odpowiedź

2023₁₀=37478 Następny rok, 2024 będzie „okrągły” w systemie ósemkowym. Będzie to bowiem rok 3750.

Zadanie 2

Jaka to liczba, która w systemie ósemkowym zapisuje się jako 2023?

Odpowiedź

20238=2∙8³+0∙82+2∙8+3=1043 Skręciłem potem w teorię grafów.

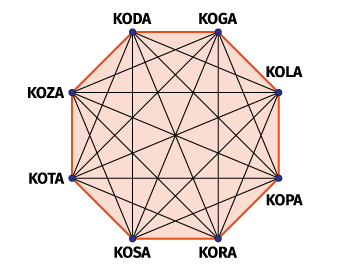
Na rysunku 3 mamy osiem słów różniących się tylko jedną literą. Dla matematyka jest to ośmiokąt foremny z przekątnymi albo graf pełny o ośmiu wierzchołkach: każdy jest połączony z każdym. Działacz sportowy może zobaczyć tu schemat rozgrywek ligowych, gdzie każda drużyna gra z każdą. Zapyta być może, jak ułożyć kalendarz takich rozgrywek. Pomoże geometria (4).

Jest taka gra, w której od jednego słowa należy przejść do innego, za każdym razem zmieniając tylko jedną literę. Jeśli nie znasz, Czytelniku, słowa KOGA, to zajrzyj do Internetu.

Zadanie 3

Przejść od PAKA przez TORT do MARS.

Podam rozwiązanie drugiej części. Można na przykład tak: TORT→KORT→KORA→KARA→MARA→MARS.

Ta zabawa nie jest daleka od matematyki. Popatrzmy na ciąg liczb binarnych: 000→001→011→010→110→111→101→100→000.

Czyli dziesiątkowych: 0→1→3→2→6→7→5→4→0.

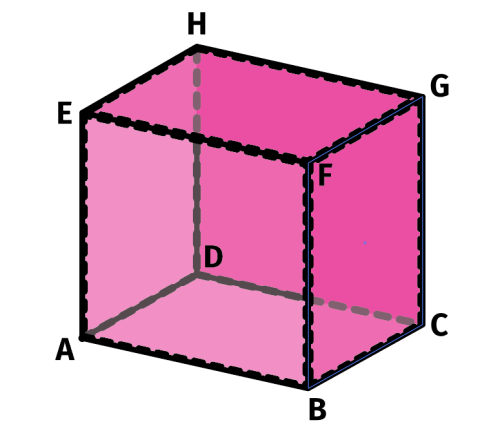
Robimy pętlę po wszystkich ośmiu układach trzech zer i trzech jedynek; wracając do liczby początkowej zero. Za każdym razem zmieniamy tylko jedną cyfrę. To tak, jakbyśmy objechali sześcian dookoła po krawędziach: ABCDHGFEA. Informatycy mówią na to „kod Graya”, dla matematyków jest to tak zwany cykl Hamiltona. Chodzi o to samo: taką zamkniętą drogę, że na każdym kroku dokonujemy tylko jednej zmiany. Ma to znaczenie w teorii sygnałów i przydaje się to tzw. error correcting codes; to znaczy kodów, które same odkrywają, że są w nich błędy i „same” się naprawiają. Ale to też temat na inny artykuł.

Wiem już od dawna, że uczniowie (nauczyciele również!) nie potrafią układać zadań. Wiem także, dlaczego tak się dzieje: zarówno jedni, jak i drudzy są nastawieni na rozwiązywanie problemów, które ktoś inny zadał. Takie jest nauczanie szkolne - w prawdziwym życiu nie zawsze tak bywa.

Wracamy na podłogę. I oto zadanie dla licealistów.

5. Cykl Hamiltona: ABCDHGFE

Zadanie 4

Zakładamy, że kąt ostry różowych deltoidów ma 36°. Wyznaczyć pozostałe kąty mozaiki na rysunku 2.

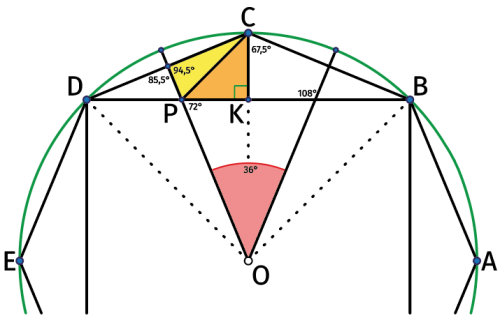
Rozwiążę tylko najtrudniejszą część - kąty białego trójkąta na rysunku 2. Zacznijmy od geometrii ośmiokąta foremnego (6). Jego kąt wewnętrzny m a 135°. Jeżeli taki ośmiokąt jest wpisany w okrąg o promieniu jednostkowym,
to jego bok ma długość .

Łatwo obliczamy kąty na rysunku 7. Wszystko otrzymujemy szybko z tego, że kąt BCD, a więc kąt wewnętrzny pięciokąta foremnego, ma 135 stopni. Gorzej jest z kątami trójkąta CPK.

Mamy:

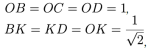
A zatem:

Z trójkąta o wierzchołku O obliczymy długość odcinka PK, a mianowicie:

I teraz znów trochę elementarnej trygonometrii:

Dalej możemy tylko wyznaczyć w przybliżeniu kąt, którego tangens jest równy właśnie tyle - da sobie z tym radę nawet kalkulator.

Otrzymamy, że kąt CPK ma miarę 51°53’24’’, czyli prawie 52 stopnie.

***

Na zakończenie zajęć postanowiliśmy z dziećmi się poznęcać nad Apolonią Inteligentną, czyli sztuczną inteligencją. Nie było łatwo - wszystko wiedziała, ale zgodnie z naszymi przewidywaniami

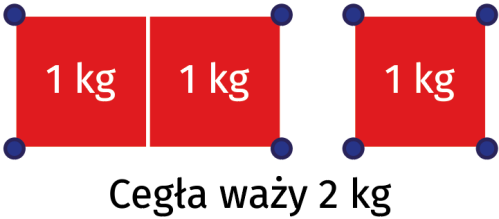
jednak nie dawała sobie rady w zadaniach z nietypowym myśleniem. Pierwsze zadanie, na którym poległa, to stary „suchar”. Cegła waży kilo i pół cegły. Ile waży ta cegła? „Rozwiązanie” na rysunku 8. Cegła waży 2 kilogramy.

Apolonia odpowiedziała tak oto (9):

Drugiego zadania Apolonia po prostu „nie przeczytała ze zrozumieniem”.

Treść jest podana w pytaniu. Poprawna odpowiedź: urodziłem się w 1980 roku, a w roku 2025 będę miał 45 lat (bo 452=2025). Teraz mam o dwa lata mniej, to znaczy 43. A ona „kręci” tak (10).

Niestety, nie powinniśmy się za bardzo cieszyć. Wkrótce Apolonia będzie jeszcze bardziej inteligentna, a jestem pewien, że już jest - tylko że w wersji utajnionej i silnie strzeżonej. Przez pewien czas będziemy mieć z nią problem w nauczaniu. Potem sami nauczymy się, jak współżyć.

Michał Szurek