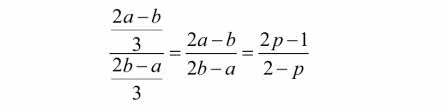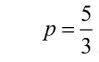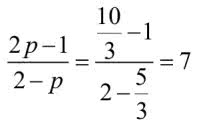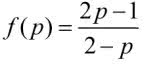W sześćdziesiąt lat później

Lektura okazała się niezmiernie ciekawa. Przypomnę, że magazyn nasz powstał jako kontynuacja czasopisma "Młody Zawodowiec", wydawanego w latach 1932-1939 i od 1946. Redaktorem naczelnym edycji powojennej był Zbigniew Przyrowski, który w 1950 roku przeforsował zarówno zmianę charakteru czasopisma, jak i tytułu, na "Młody Technik" właśnie. Na stanowisku redaktora naczelnego Zbigniew Przyrowski pozostał aż do emerytury w 1981 roku. Był nieoceniony.
Imponuje lista autorów tamtego numeru - znani wówczas profesorowie, inżynierowie i naukowcy. Krótko o najważniejszych i najciekawszych tekstach. Numer otwiera artykuł "Najbliższe pespektywy Astronautyki", Zbigniewa Pączkowskiego (1912-1993, ówczesnego prezesa Polskiego Towarzystwa Astronautycznego). Jest to sprawozdanie z XI Międzynarodowego Kongresu Astronautycznego (Sztokholm, 15-20 sierpnia 1960). W artykule znajduje się stwierdzenie, że lądowania na Księżycu należy się spodziewać w latach 1967-1970. Przypomnę, że Jurij Gagarin poleciał w Kosmos 12 kwietnia 1961 roku, a Neil Armstrong dokonał "małego kroku człowieka, a olbrzymiego skoku ludzkości" 21 lipca 1969 r.
Z innych interesujących tematów należy wspomnieć obszerny tekst "Elektronika usprawnia samochody" autorstwa Andrzeja Sowińskiego. Opisany jest tam system automatycznego kierowania samochodem, już wtedy (!) testowany w USA. Odnotujmy jeszcze, że Andrzej Sowiński (1922-1996), profesor Politechniki Warszawskiej, wydał pierwszą w Polsce książkę o telewizji ("Zasady telewizji", 1957 r.). W numerze jest też artykuł o … konieczności rozbudowy portu lotniczego w Warszawie (jego autorem jest inna sława tamtych lat: architekt Witold Szolginia, 1923-1996).
Inną ciekawostką, może daleką od matematyki, ale jak najbardziej mieszczącym się w naszym profilu, jest pomysł z opowiadania s.-f., wtedy zamieszczanym w każdym numerze (nawet Stanisław Lem pisywał do nas!). Otóż na granicy Polski, w Tatrach, ustawiono człekokształtne "roboty", Wojtki, które nie przepuszczały nikogo - ale w można było "w kantorze ruchu granicznego" wykupić żeton na przejście. Dla zwierząt górskich granica była otwarta, na przykład dla świstaków. Zręczny chłopiec góralski nauczył się imitować ten świst i … wojsko dostało rozkaz, żeby udoskonalić Wojtka. Zwracam uwagę, że mur berliński powstał w niecały rok po ukazaniu się tego opowiadania. Autorem opowiadania był Jan Stanisław Kopczewski (1929-2016), członek komitetu redakcyjnego "Młodego Technika" w latach 1955-1969, naprawdę bardzo ceniony działacz i autor książek historycznych dla młodzieży. Cóż, młodzi Czytelnicy nie pamiętają i nawet nie są w stanie sobie wyobrazić psychozy lat sześćdziesiątych, w szczególności roku 1962, gdzie milimetry dzieliły nas od wojny atomowej.
W rubryce "Nowe książki" redakcja poleca "Reportaż z XXI wieku". Cytuję: "Wybierając się w XXI wiek, autorzy (Michaił Wasiljew i Siergiej Guszczew) udali się do gmachu Akademii Nauk ZSRR". Gdybym znalazł tę książkę… Byłaby pasjonująca! Próbuję w serwisach aukcyjnych. Zaś w dziale "Na warsztacie" Stanisław Sabat opisuje szczegółowo, jak zbudować mały skuterek. Skomentuję to krótko: potrzeba jest matką wynalazków. Autor zaznacza, że "zastrzega się prawa autorskie w razie podjęcia produkcji seryjnej".
Bardziej o matematykę zahacza krótka wzmianka o Międzynarodowym Towarzystwie Płaskiej Ziemi. Cytuję: "jego sekretarz, Samuel Shenton, 58-letni Anglik, w bardzo prosty wytłumaczył wszelkie wypadki tajemniczych zaginięć osób, których nie udało się odnaleźć służbom bezpieczeństwa. Pan Shenton wystąpił nawet w telewizji brytyjskiej, ale zdenerwował się, bo jego zdaniem próbowano go tam ośmieszyć. Otóż zdaniem Shentona, osoby te doszły do brzegu Ziemi i nieopatrznie się przechyliwszy, spadły w przepaść. Zdaniem członków Towarzystwa, nasz glob ma kształt talerza. Fakt, że podróżnik, odbywający podróż dookoła świata wraca do punktu wyjścia - według Shentona niczego nie dowodzi. Mucha spacerująca po brzegu talerza też dojdzie do punktu wyjścia".
Podobno i dziś, a więc w 60 lat później, towarzystwa płaskoziemców, antyszczepionkowców i zaprzeczających istnieniu Covida mają się całkiem dobrze. Z tymi pierwszymi ja nawet sympatyzuję, bo są mili i nieszkodliwi. Zastanówmy się przez chwilę (da się to wszystko wyliczyć matematycznie), co by było na Ziemi mającej kształt płaskiego talerza. To jest nawet dobry temat literacki, ale skupię się na matematyce. Przyjmijmy, tak "na rybkę" średnicę owego talerza na 10000 km, a grubość na 10 km. To i tak bardzo cieniutki placek.
Prawa fizyki (odkryte przez rodaka pana Shentona, niejakiego Newtona) mówią, że obiekty fizyczne przyciągają się z siłą odwrotnie proporcjonalną do kwadratu odległości między nimi. Gdy stoimy na kulistej Ziemi (jej promień to 6371 km), wtedy każda jej cząsteczka przyciąga każdy fragment naszego ciała. Wektor tej siły jest skierowany do środka Ziemi, czyli dla nas pionowo w dół. To właśnie grawitacja daje nam poczucie pionu, a horyzont - poziomu. Dlatego kąt 90 stopni wydaje się nam prosty - i tak jest przecież nazywany.
A jak wygląda sprawa przy brzegu owego talerzyka? Wektor grawitacji jest skierowany do środka masy całej planety, a więc jest niemal poziomy. Co to znaczy? To proste: jesteśmy na prawie pionowej ścianie. Jak to na pionowej ścianie, każdy ruch grozi upadkiem w dół. Możemy pokonać te trudności i wyjść na brzeg, na rancik naszej olbrzymiej monety i wtedy rzeczywiście możemy spaść w dół na drugą stronę. Shenton miał jednak rację.
Teraz już konkretnie o zadaniach matematycznych z numeru październikowego 1960, a właściwie o jednym, w kilku odmianach. Aż podskoczyłem z uciechy, gdy je zobaczyłem. Wspomnę też, że tamten kącik matematyczny w "Młodym Techniku" (aż do około 1972 r.) prowadził przez wiele lat Stanisław Kowal, niedoceniany popularyzator, autor kilku ciekawych pozycji. Polecam, np. "Koło Matematyczne i Opowieści Profesora X".
Z treści zadania trudno od razu zgadnąć, co mi się tak spodobało. Ale o tym jest właśnie merytoryczna, matematyczna część artykułu. Pamiętajmy: jest rok 1960, samochody w Polsce to rzadkość i niedostępny luksus, drogi są … jeszcze gorsze niż teraz, a gospodarka uspołeczniona jest przedstawiana jako coś o niebo lepszego od prywatnej. Przepisuję.
Państwowe Gospodarstwo Rolne (PGR), Kółko Rolnicze (KR) i Stacja Maszynowa (SM) znajdowały się w pewnej odległości od szosy i sąsiadowały ze sobą. Dla ułatwienia łączności z gminą, trzy te jednostki gospodarcze postanowiły własnymi siłami, wspólnie, zrobić sobie dojazd do szosy. PGR dostarczyło na budowę dojazdu 20 fur kamienia, SM pięć ciężarówek równających się 25 furom kamienia, a KR w zamian za kamień dało po dokładnym obliczeniu 4500 zł, które stanowiły wartość jego udziału w budowie dojazdu. Tę gotówkę należało podzielić między PGR i SM. Ale w jaki sposób?
PGR zaproponowało podzielić 4500 zł na dwie równe części. Ale SM nie zgodziła się i zaproponowała podział pieniędzy proporcjonalnie do dostarczonych fur kamieni: PGR za 20 fur - 2000, SM za 25 fur - 2500 zł.
Księgowy Kółka Rolniczego, który przysłuchiwał się tej sprzeczce, uśmiechnął się i powiedział:
- Nie, panowie! Zarówno podział na połowy, jak i proporcjonalny do liczby fur jest niesłuszny. Ja wam tak podzielę te 4500 zł, że nikt nie będzie pokrzywdzony. Jaki podział zaproponował księgowy?
Zauważmy na marginesie, że dziś nie zakładalibyśmy, że w zarządach są sami mężczyźni, a księgowość prowadziłaby "raczej na pewno" kobieta. Rozwiązania zadania nie przytoczę. Po przeczytaniu artykułu do końca każdy znajdzie je samodzielnie.
W dydaktyce matematyki istnieje pojęcie "zadań izomorficznych". To zadania mające różną fabułę, ale tę samą treść matematyczną. Jeżeli mamy obliczyć, ile trzeba wziąć octu 15% a ile octu 6%, żeby otrzymać litr octu 10% - to każdy powinien pojąć, że jest to izomorficzne z zadaniem o mieszaniu cukierków za 15 zł z cukierkami za 6 zł tak, żeby otrzymać kilogram mieszaniny po 10 zł. Uczniowie: czy potraficie rozwiązać?
I otóż zadanie Stanisława Kowala o wspólnej budowie drogi pojawiło się w Polsce w książce "Lilavati" Szczepana Jeleńskiego (pierwsze wydanie 1930 r.) - od razu w trzech wersjach. Warto je przytoczyć. Zachowując oryginalną pisownię, przepisuję dwie:
Dwaj chłopcy, Michał i Paweł, zbierali w lesie chrust i mieli spożyć śniadanie. Michał miał 4 kromki chleba, a Paweł 7. W tej właśnie chwili podszedł do nich podróżny i zwrócił się ze słowami:
- Zabłądziłem, chłopcy, w tym lesie, do wsi daleko, a głód mi dokucza, podzielcie się ze mną tem, co posiadacie.
- Zgoda, niech pan siada, czem chata bogata, tem rada, odpowiedzieli życzliwie.
Po śniadaniu podróżny sięgnął do kieszeni i wydobył srebrną złotówkę i niklową dziesięciogroszówkę. Wręczają pieniądze chłopcom, powiedział:
- Wyście się ze mną podzielili całem waszem śniadaniem, ja daję wam też wszystko, co mam.
Gdy podróżny oddalił się, chłopcy zaczęli się spierać.
- Według mnie, twierdził Michał, pieniądze powinniśmy podzielić po połowie.
A Paweł z gniewem zaprzeczył:
- Za 11 kromek chleba, jakie mieliśmy, zapłacono nam 1 zł 10 gr. Za jedną więc kromkę wypada 10 groszy. Tyś miał 4, a więc na ciebie wypada tylko 40 groszy, moich było 7 kromek, rzecz jasna, że mam prawo do 70 groszy.
Który z chłopców prawidłowo obliczył?
Dwóch stróżów nocnych gotowało sobie kaszę; jeden wsypał do garnka 200 gram kaszy, drugi 300. Kiedy kasza była już gotowa, podszedł do nich trzeci stróż i poprosił, by mu pozwolili wziąć udział w wieczerzy za zapłatą. Posiliwszy się, zapłacił 50 groszy. Jak powinni podzielić otrzymane pieniądze dwaj właściciele kaszy?
Czwartą wersję zadania znałem już przed 1960 rokiem, właśnie z Lȋlȃvatȋ. Tak, tak, młody Czytelniku. Twoi dziadkowie mogą być moimi rówieśnikami. Ale co to za dziwne słowo? Otóż nasze (moje i Twoich dziadków!) pokolenie wychowało się tej książce. Līlāvatī, Lȋlȃvatȋ, लीलावती, to imię biegłej w matematyce dziewczyny hinduskiej, prawdopodobnie córki sławnego matematyka hinduskiego Bhāskary Acāryi (1114-1185). Warto przytoczyć fragment przedmowy z 1930 roku:
Lȋlȃvatȋ - to znaczy urocza, czarująca! Taką zapewne była owa dziewczyna hinduska, obdarzona niepospolitym talentem matematycznym; ale taką jest przede wszystkiem sama matematyka!
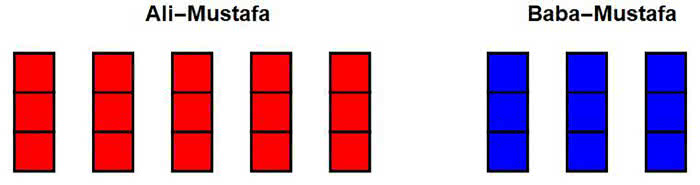
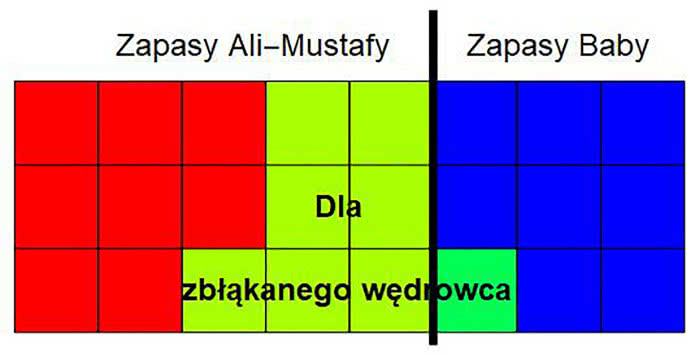
Ale długą brodę miało to zadanie i 90 lat temu - już jako dawne przytacza je W. W. Rouse Ball w 1892 r. Rozpoznamy natychmiast, że jest ono izomorficzne z zadaniem o PGR, KR i SM, o chłopcach w lesie i o stróżach nocnych. Otóż dwaj Arabowie, nazwę ich tutaj Ali-Mustafa i Baba-Mustafa, ratują głodnego podróżnego na pustyni, dzieląc się z nim swoimi sucharami. Ali ma pięć, Baba trzy. Dzielą każdy na trzy części - wtedy na każdego przypada po osiem cząstek. Spożywają razem, a uratowany wędrowiec odwdzięcza się ośmioma złotymi monetami. Ali i Baba spierają się, czy podzielić je solidarnie i równo, po cztery, czy proporcjonalnie do wkładu, czyli 5:3. Mądry kadi (= sędzia) rozstrzyga spór i ku zdumieniu wszystkich dzieli je w stosunku 7:1 - oczywiście 7 dla Ali, 1 dla Baby. Argument jest bardzo prosty. Z ośmiu kawałków, jakie zjadł uratowany wędrowiec, aż siedem pochodziło z zapasów Ali-Mustafy. Rysunki wyjaśnią to najlepiej.
Zadania te są mądrzejsze, niż nam się wydaje. Rozwiążmy najpierw problem ogólniejszy. Ala-Mustafa ma a sucharów, Baba-Mustafa b. Zatem Ala, Baba i Wędrowiec zjadają w sumie a+b, każdy po
W jakiej proporcji pozostają wkłady obu darczyńców? Trzeba podzielić te dwa ułamki. Oznaczę jeszcze stosunek a:b przez p.
Czyli jest tak: jeżeli wkłady wspólników pozostają w stosunku p do jednego, to zyski należy dzielić w stosunku
Pamiętajmy tylko, że korzystają po równo wszyscy (łącznie z dającymi). Przede wszystkim sprawdźmy wynik ze zdrowym rozsądkiem. Notabene, takiego sprawdzania nie mogę nauczyć uczniów i studentów. Niechlubny rekord dzierży studentka geografii, której na kolokwium "wyszło", że biegun północny jest o 114 km od Warszawy. A jakże, podkreśliła nawet wynik na czerwono i zadowolona wyszła z sali - no, bo przecież zadanie zrobiła.
Co u nas? Jeżeli p=1, to znaczy, że obaj wspólnicy dają ten sam wkład. Zgadza się, wartością napisanego wyżej ułamka jest 1, równy podział. Jeżeli jednak Ali miał a=5 sucharów, zaś Baba miał b=3, to mamy
Podstawmy:
Kadi miał rację: siedem sztuk złota dla Ali, jedna dla Baby.
Funkcja
jest okropna.
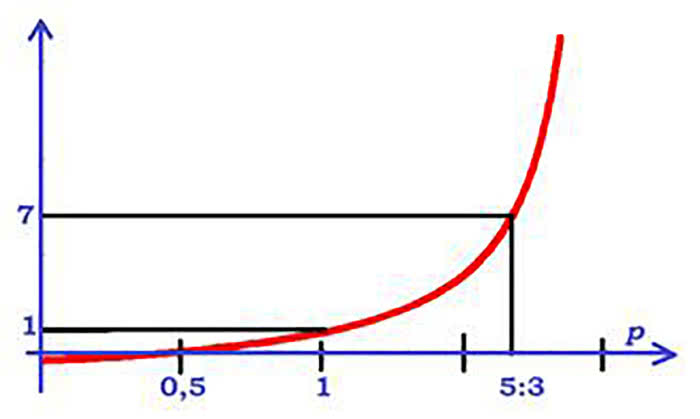
Co w niej takiego strasznego? Spójrzmy na wykres. Wynika z niego na przykład, że gdy p zbliża się do 2, wartość funkcji gwałtownie rośnie. Sprawdźmy. Jeżeli p=1,9, to f(x)=29. A zatem, gdyby Ali miał 19 sucharów, Baba 10, to z otrzymanych np. 30 złotych monet, na Ali-Mustafę przypadnie 29, na Babę tylko jedna! Jeszcze większa pozorna dysproporcja.
Dla
otrzymujemy zero. Co to znaczy?
To jasne: wszystkie pieniądze idą do Baby. Wartości ujemne znaczą oczywiście, że nie tylko, że jeden nich zabiera wszystkie otrzymane pieniądze, to jeszcze drugi mu dopłaca, bo sam miał za mało, żeby przeżyć.
Matematycznie wszystko jest w porządku, ale … Teraz bardziej doceniamy wkład każdego członka zespołu we wspólne dzieło. Wiadomo, że wkład Roberta Lewandowskiego w ewentualne zwycięstwo Polski na kolejnych mistrzostwach świata w piłce nożnej (jeżeli się odbędą!) prawdopodobnie będzie największy. Ale wszyscy dostaną takie same złote medale.
W pracach naukowych nie podaje się procentowego wkładu poszczególnych autorów, a wszelkie próby wyliczenia tego są śmieszne. To uznanie dla team-work pochodzi z USA. Nie wszystko, co amerykańskie, jest od razu złe. Uff, wrócę do matematyki.
Najważniejsze w tym całym zadaniu jest świetna ilustracja pewnego zjawiska dotyczącego gry na giełdzie. Oczywiście matematyka nie zapewnia sukcesu w spekulacjach giełdowych. Może nawet przeszkadza. Matematyka finansowa sprawdza się, gdy wszystko idzie normalnie. Żeglujemy po spokojnym jeziorze. Widać to było w światowym kryzysie finansowym z 2008 roku. Wszyscy analitycy byli zgodni, że nie było najmniejszych podstaw do paniki i załamania się gospodarki światowej - a gospodarka najwyraźniej postanowiła nie brać tych opinii pod uwagę. Ale znów odbiegłem od tematu. Chodzi mi o tak zwany efekt dźwigni. Pojawia on się tam, gdzie małe zmiany jakiegoś parametru powodują duże zmiany efektu. Na efekcie dźwigni biedni biednieją, a bogatym przybywa. Efekt ten opisywano od dawna w popularnych książkach matematycznych; niektórzy doszukują się go i w Biblii. To żart, bo tam naprawdę chodzi o dar wiary:
Kto ma, temu będzie dodane i obfitować będzie. Ale kto nie ma, i to co ma będzie od niego odjęte. [Mt 13].
To właśnie efekt dźwigni powoduje, że niewielka różnica w inwestycjach (np. 5 do 3) powoduje duże różnice wypłaty (7 do 1). Dotyczy to opcji. Na świecie możliwość spekulacji opcjami istnieje od co najmniej pół wieku, w Polsce od 2005 roku. Podręczniki matematyki finansowej definiują opcję jako wtórny instrument finansowy, odzwierciedlający instrument zasadniczy, za jaki pojmuje się akcje spółek notowanych na giełdzie. Opcja kupna to zobowiązanie, że osoba wystawiająca tę opcję sprzeda mi coś (na przykład samochód albo worek ziemniaków) w określonym czasie, za ustaloną w opcji cenę. Opcja sprzedaży to obietnica kupna czegoś ode mnie (np. zboża od rolnika) za ustaloną cenę. Istotą sprawy jest to, że z opcji mogę, lecz nie muszę skorzystać. Jeśli cena kupna, czy sprzedaży mi nie odpowiada, nie muszę z opcji korzystać; jeśli jednak cena mi odpowiada, wtedy korzystam z posiadanej opcji. Jest to moje prawo. Za nabycie tego prawa muszę zapłacić. Ile? To właśnie jest jeden z trudnych problemów matematyki finansowej. Tak trudny, że za jego rozwiązanie dano nagrodę Nobla z ekonomii (1997, Fischer Black, Myron Scholes). Ponieważ w Internecie można teraz znaleźć dowolne głupstwo, da się i znaleźć opinię, że to była niesłuszna nagroda. Klasyczna mieszanina hejtu i niezrozumienia.
Bardzo konkretny przykład.
Kupujemy coś za 100 zł, chomikujemy i czekamy na zmianę ceny. Podskoczyła, do 130 zł. Sprzedajemy. Stopa zysku wynosi 30%. Jeżeli jednak uwierzymy przepowiedniom, że cena tego czegoś zmieni się ze 100 zł na 110, to opcja kupna ich za 101 złotych jest warta 9 złotych. To jest cena równowagi. Nie warto kupować za więcej. Kupujemy opcję. Okazuje się jednak, że cena skacze na 130 zł. Posiadaną opcję możemy sprzedać za co najwyżej 29 zł. Wartością opcji kupna za 101 zł jest (cena równowagi) 29 zł. Czyli zainwestowane 9 zł dało przychód 29 zł (a zatem dochód 20 zł). Stopa zysku jest zatem równa 222,22%. Gdyby jednak cena wzrosła tylko do 113 zł, to opcję kupna za 101 zł możemy sprzedać co najwyżej za 12 zł (dochód: 12–9=3 zł), osiągając stopę zwrotu 33%, większą niż przy sposobie bez opcji (kupno za 100, sprzedaż za 113). Gdyby cena wzrosła tylko do 105 zł 50 gr, to na strategii "opcyjnej" jesteśmy stratni: opcję która nas kosztowała 9 zł możemy odsprzedać tylko za 4,5 zł. Jeśli cena spadnie do 95 zł, to na strategii bezpośredniej tracimy 5 zł (5%), a na opcjach mamy "stopę zwrotu" równą minus 100 procent: opcje są warte zero i tracimy na nich wszystko.
***
A skoro mowa o pieniądzach, to wrócę jeszcze do tego numeru "Młodego Technika" sprzed 60 lat. Do działu "Pomysły genialne, zwariowane i takie sobie" (strona 96) pan Kazimierz Piotrowski z Warszawy nadesłał pomysł "automatycznego dystrybutora" - automatu, który po wrzuceniu bilonu lub uprzednio zakupionego żetonu wydawałby stosowną porcję paliwa. Samoobsługowe stacje benzynowe, pisał pan Kazimierz, mogłyby pracować nawet całą dobę!
Koncerny naftowe (Shell, BP, Texaco, Łukoil, Exxon i inne giganty a nawet i Orlen) chyba nie dostrzegły, że to na łamach "Młodego Technika" ten pomysł się pojawił. Redakcja powinna skierować sprawę do międzynarodowego trybunału i domagać się tantiemów (z odsetkami!), z których oczywiście co najmniej 95 % należy się panu Kazimierzowi, albo jego spadkobiercom. To, co zostanie (szacuję na kilkanaście milionów) zużyjmy na potrzeby naszego magazynu, a ja za podpowiedź poproszę tylko symboliczną złotówkę (z odsetkami za 60 lat!). I taki będzie efekt dźwigni finansowej i pożytek z czytania starego "Młodego Technika". A dla młodych (i niekoniecznie młodych) Czytelników zadanie: to ile dostanę teraz pieniędzy, jeżeli odsetki będą 5% w skali rocznej? Czy wystarczy mi na kawę na Rynku Głównym w Krakowie? A może na kawę i lody?
Michał Szurek
Zobacz także:
Kolorowa matematyka
Malarstwo, muzyka, matematyka
Równania, kody, szyfry, matematyka i poezja