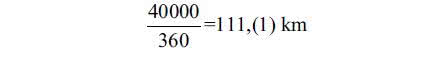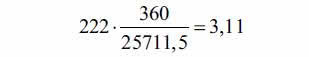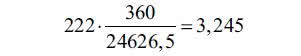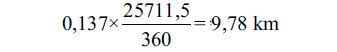Krzywe jest piękne

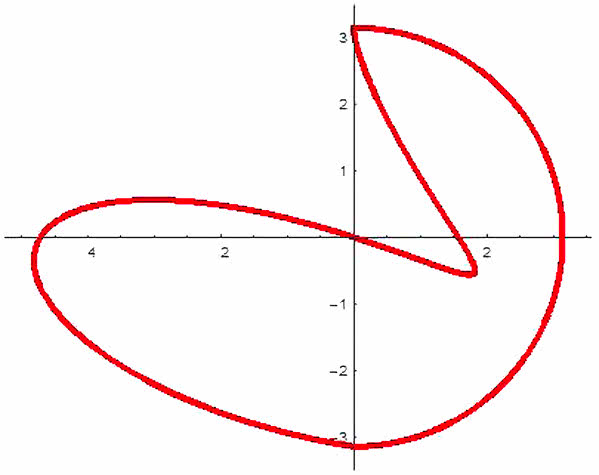
Obejrzałem potem w Google Maps ten wjazd. Był właściwie sprofilowany. Co to znaczy? Nie trzeba być matematykiem, żeby rozumieć, że linia prosta ma krzywiznę zero, natomiast okrąg (brzeg koła) ma stałą krzywiznę. Każdy też rozpozna, gdzie krzywizna jest większa lub mniejsza (1).
Fizycy mówią często o zakrzywieniu przestrzeni. Czy nasz Wszechświat jest płaski, czy może ma krzywiznę dodatnią lub ujemną? Trudno to sobie wyobrazić, bo jakże cały świat może być zakrzywiony? Nie sama powierzchnia Ziemi, tylko cała przestrzeń, w której żyjemy?
W młodości podróżowałem często nocnym pociągiem, nierzadko na stojąco. Wyobraźmy sobie taki pociąg, w dodatku zimą - okna zaparowane, nic nie widać. Nic się nie zmienia, tylko wagony podskakują na złączach szyn. Czy możemy wyczuć, że tor zakręca? Oczywiście - jeżeli "coś" nas przyciśnie do lewej ściany, to znaczy, że zakręcamy w prawo.
"przedobrzony" - w rzeczywistości wykorzystuje się tylko drobny fragment krzywej.
Podobnie wyczujemy zakrzywienie, gdy z zawiązanymi oczami będziemy chodzić po łagodnie pagórkowatej łące ("łagodnie" dla naszego bezpieczeństwa). Jeżeli nagle będzie nam ciężej iść, to znaczy, że teren się zakrzywia. W obu przypadkach do stwierdzenia krzywizny potrzebna jest pewna siła (siła bezwładności dla pociągu, grawitacja dla chodzenia po ciemku na łące).
Od krzywizny Wszechświata zależy jego przyszłość, ale nas już wtedy i tak nie będzie.
Ogarnąć kulistość
Drugim przyczynkiem do tego artykułu jest zadanie, które dałem jako pracę domową studentom pierwszego roku studiów informatycznych. Zaskoczyło mnie, że było ono dla nich bardzo trudne. A jest łatwe i pouczające.
Jak wiemy, Ziemia nie jest płaska - w co trudno było uwierzyć naszym prapradziadkom. Zresztą, co ich to mogło obchodzić? Nie obchodziło nawet Sherlocka Holmesa, znanego przecież ze swojej inteligencji i domyślności.
Wybitny matematyk lwowski, a potem wrocławski, Hugo Steinhaus (1888-1972) mówił, że glob ziemski jest niepraktycznie zbudowany. Spośród bardzo wielu aforyzmów Steinhausa przytoczę jeden:
Kula u nogi? Ziemia!
Kulistość Ziemi daje wiele ciekawych wątków do zadań geometrycznych. Matematyczna Ziemia jest kulą o promieniu 6371 km i obwodzie 40 000 km. Te dane nie są idealnie zgodne - kula o podanym promieniu ma obwód 2πR=2·3,14159·6371=40030,2 km. Ponadto nie uwzględniamy spłaszczenia Ziemi, też zresztą niewielkiego.
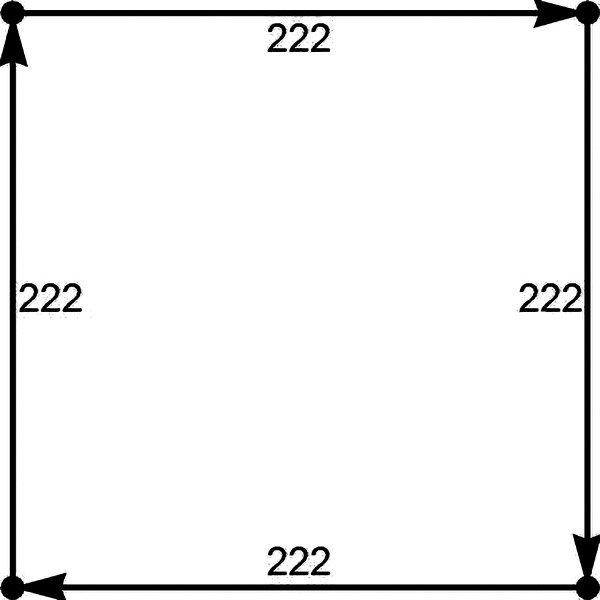
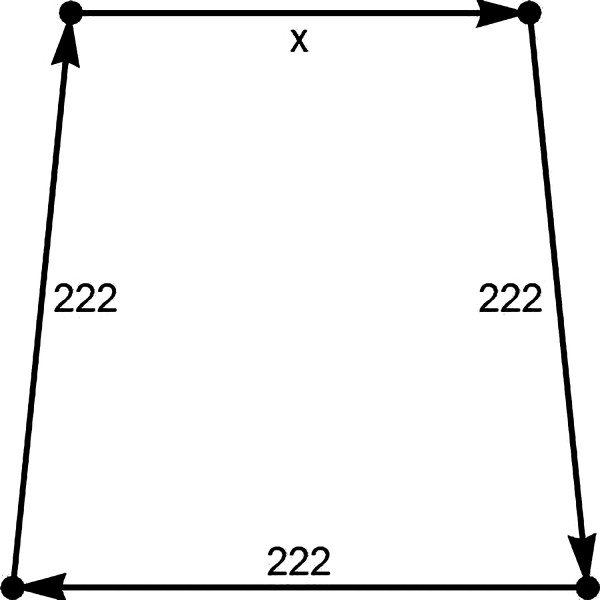
Zadanie 1. Z lotniska im. Jana Pawła II w Balicach (czyli w Krakowie) wyleciał na północ samolot. Przeleciał 222 km, potem skręcił na wschód i lecąc stale na wschód przeleciał też 222 km, następnie skręcił w prawo na południe i też przeleciał 222 km, wreszcie pokonał 222 km, kierując się na zachód. Pilot, ku swemu zaskoczeniu, zobaczył lotnisko, ale z dużej odległości. Jak to wyjaśnić? Gdzie znajduje się samolot?
Rozwiązanie. Gdyby Ziemia była płaska, pilot wykonałby lot po obwodzie kwadratu, a więc zakończył lot w punkcie startu (3). Można łatwo wyliczyć, że 222 km na północ od Balic to okolice Łowicza. Ziemia nie jest jednak płaska.
Kąt pełny ma 360 stopni, a zatem 1 stopień na równiku to
co zaokrąglimy do 111. Zatem 222 km to dwa stopnie - na równiku i na każdym południku.
Wszystkie południki zbiegają się w biegunach. Im dalej od równika, tym równoległobok jest krótszy. Na biegunie "nie ma go w ogóle" - jest jednym punktem. Bieguny nie mają długości geograficznej. Szerokością geograficzną biegunów jest ±90 stopni. Samolot leciał więc po "zakrzywionym równoległoboku". Gdyby chciał wrócić dokładnie do punktu wyjścia, musiałby na równoleżniku 52 przelecieć nieco mniej niż 222 km (4).
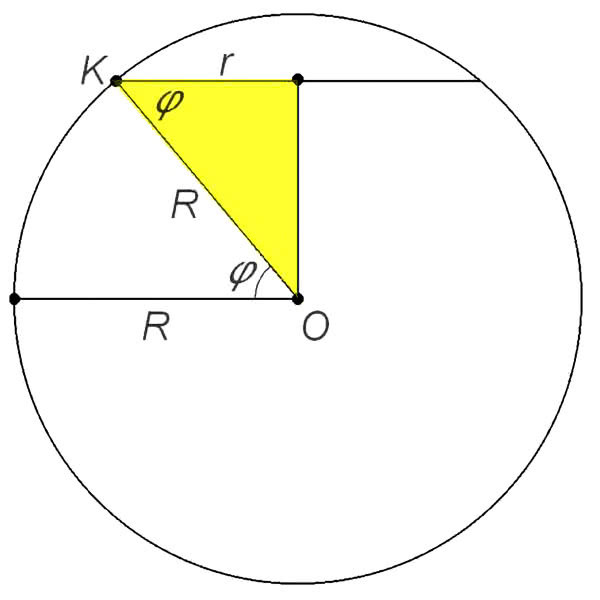
Najpierw wyznaczmy długość równoleżnika odpowiadającego szerokości geograficznej φ. Na rys. 5 widzimy Ziemię w przekroju. Promień r równoleżnika, na którym leży punkt K, jest równy R cos φ, zatem cały równoleżnik ma długość 2·π·r=2·π·R·cos φ.
Google Maps podaje współrzędne lotniska w Balicach - szerokość geograficzna to w bardzo dobrym przybliżeniu 50 stopni (szerokości północnej). Szerokość oznaczamy zwyczajowo grecką literą φ. Gdy φ=50°, mamy r=r50=40000·cos 50°=25711,5 km. Równoleżnik Balic ma 25711,5 km. Na szerokości 52 stopnie podobne wyliczenie daje 24626,5 km.
Ilu stopniom odpowiada 222 km na szerokości 50°?
Skoro 360 stopni daje 25711,5 km, to 222 km odpowiada
stopnia. Na szerokości 52 to już jest
stopnia. Nie będziemy zamieniać na stopnie i minuty kątowe.
Zadanie 2. A może jednak? Wyraź 3,245 stopnia w stopniach, minutach i sekundach kątowych.
Wracamy do samolotu. Jak leciał? Po trzech odcinkach lotu wrócił na tę samą szerokość geograficzną (Balice, 50 stopni), ale o ułamek stopnia długości dalej na wschód, w przybliżeniu o 3,245-3,108=0,137 stopnia. Na szerokości geograficznej Balic jest to
Rzut oka na mapę pokazuje, że samolot jest nad Wzgórzami Krzesławickimi. Widzi już Balice…
Zadanie 3. Na jakiej szerokości geograficznej równoleżnik ma długość 222 km?
Zadanie 4. Lotnisko w Sydney w Australii ma skrót SYD. Szerokość geograficzna tego miejsca to 32°, oczywiście południowa. Samolot wylatuje z Sydney, leci 222 km na północ, potem 222 km na wschód, następnie 222 km na południe i znów 222 km na zachód. Czy znajduje się przed, za, czy dokładnie nad lotniskiem?
Zadanie 5. Lotnisko w Anchorage (Alaska, USA) ma szerokość geograficzną północną 61°. Samolot wylatuje z niego i leci najpierw na południe aż do równika, potem wzdłuż równika na zachód i z powrotem do Anchorage po południku. Okazuje się, że trasa jest trójkątem równobocznym. W którym miejscu samolot dolatuje do równika i opuszcza go?
Zadanie 6. Wiemy, że przy locie transkontynentalnym z Japonii do USA "zyskujemy jeden dzień" - przekraczamy międzynarodową linię zmiany daty i cofamy się o 24 godziny. Tak jest zawsze, gdy podróżujemy "ze słońcem" - z zachodu na wschód i przekraczamy ową linię. Przeżywamy od początku ten sam dzień. Przeciwnie przy podróży powrotnej, z USA do Tokio - tracimy jeden dzień. Po raz pierwszy skorzystali z tego uczestnicy wyprawy Ferdynanda Magellana. "Przywieźli" do Europy czwartek, gdy na kontynencie był już piątek. Było to ważne z powodów religijnych i ściśle wtedy przestrzeganych postów. Czy obowiązuje mnie wtedy pokładowy czwartek, czy kontynentalny piątek? Skorzystał na tym też Fileas Fogg w powieści Juliusza Verne’a "W osiemdziesiąt dni dookoła świata". Dzięki tej różnicy wygrał astronomiczną wtedy kwotę 20 tys. funtów.
W XXI wieku zapytuję "wujka Google’a" o szybkie połączenie z LAX do NRT, czyli z Los Angeles do Tokio. Oto jedna z możliwości: wylot 16 grudnia 4:25 po południu, przylot tego samego dnia 10:40 przed południem. Zyskujemy kilka godzin życia, za głupie tysiąc dolarów. Czyż to nie fantastyczne?
Ale w związku z tym zadanie. Jedziemy w pobliże bieguna - tak, żeby obiegnięcie go zajęło nam godzinę. Biegamy naokoło, z zachodu na wschód. Co godzinę młodniejemy o jeden dzień. Biegając dostatecznie długo, możemy odmłodnieć tak bardzo, jak chcemy… Możemy też latać samolotem - za każdym razem cofamy się o prawie całą dobę w czasie, bo przecież przekraczamy linię zmiany daty za każdym razem w jedną stronę. Jak jednak czujemy, nie cofnie nas to do czasów dzieciństwa, ani nawet o tydzień. Popełniamy zatem błąd w rozumowaniu. Ale gdzie?
Zadanie 7. Jak daleko nasz samolot powinien lecieć nad Mazowszem, żeby po zwrocie na południe i po przebyciu 222 km znaleźć się nad Balicami?
Sprawiedliwość na bieżni
Trzecim powodem wyboru tematu artykułu były niedawne mistrzostwa świata w lekkoatletyce. Polska sztafeta żeńska 4×400 m zdobyła srebrny medal. Jako kilkunastolatek chodziłem na Memoriał Kusocińskiego - zawody gromadziły wtedy dziesiątki tysięcy kibiców. Fascynowało mnie zawsze "wyrównanie".
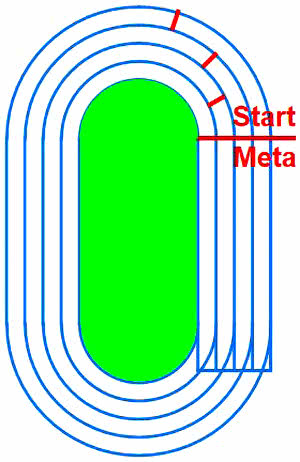
Sprawę łatwo pojąć - zawodnik biegnący po torze zewnętrznym ma dłuższą drogę po łuku. Musi mieć wobec tego przesunięty start. Wydawało mi się wtedy, że wyliczenie takiego wyrównania jest skomplikowane. Okazuje się, że… istotnie jest, ale nie z powodu matematyki, a przepisów Międzynarodowego Stowarzyszenia Federacji Lekkoatletycznych (IAAF).
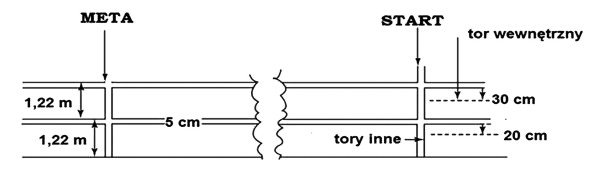
Przepis nr 160 IAAF precyzuje, że tory powinny mieć szerokość 122 cm, wraz z oddzielającą je linią. Inny paragraf zaleca (choć nie nakazuje), by proste i łuki miały tę samą długość.
Co znaczy ten ostatni warunek? To, że prosta finiszowa i tzw. przeciwległa mają po 100 m, a na każdy z łuków też przypada po 100 m. Są to zatem łuki o promieniu
Porównajmy teraz dwa sąsiednie tory, np. pierwszy i drugi. Skoro ten pierwszy ma 400 m, a szerokość toru wynosi 122 cm, to promień łuku drugiego toru wynosi 31,83+1,22=33,05 m. Zawodnik robi dwa pełne półokręgi, a zatem biegnie po łukach 2∙π∙33,05=207,66 m, zamiast 200. Wyrównanie ma wynosić 7,66 m.
Inaczej jest w sztafetach 4×400 m. Zawodnicy zbiegają do krawężnika po przebyciu 500 m, czyli po przebiegnięciu półtora łuku. Wyrównanie dla sąsiednich torów wynosi zatem półtora razy więcej, tzn. aż 11 m 49 cm. Gdy startuje osiem drużyn, bloki startowe zawodnika z zewnętrznego toru znajdują się ponad 80 m przed tym z wewnętrznego. Na mecie wszystko się jednak wyrównuje.
Wkręcić się jak po śrubie
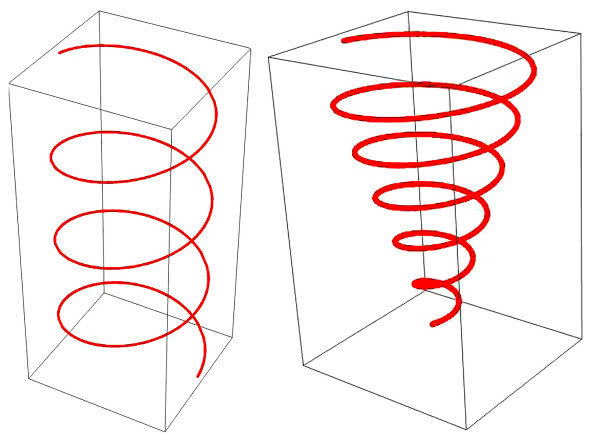
I jeszcze wycieczka w przestrzeń. Gdy wjeżdżamy na piętrowy parking pod dachem, wspinamy się łukowatymi podjazdami. Wkręcamy się jak po śrubie. Nie zmieniamy położenia kierownicy. Jedziemy po krzywej przestrzennej o stałej krzywiźnie. Jest tylko jedna taka krzywa. Coraz częściej nazywana bywa mylnie helissa, a tymczasem poprawną nazwa jest, niestety, mniej poetyczna linia śrubowa.
Powstaje ze złożenia ruchu jednostajnego obrotowego z jednostajnym postępowym. Warto zdać sobie sprawę ze znaczenia faktu, że istnieje tylko jedna krzywa, która może się ślizgać sama po sobie. Śruby muszą mieć… kształt linii śrubowej. Matematyka nie daje technice nic innego do wyboru.
Zaprotestują tu stolarze i ci wszyscy, którą lubią prace z drewnem - przecież wkręty do drewna są stożkowe! Tak, ale dlatego nadają się tylko do drewna. Rozpychają materiał, w który się wkręcają. Z blachą nie dadzą sobie rady.
Zobacz także:
Wycieczka w nierzeczywisty świat matematyki
Urok liczb nieparzystych