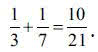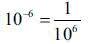Lem, Tokarczuk, Kraków, matematyka

Zjazd był bardzo uroczysty, pełen imprez towarzyszących (łącznie z występem Jacka Wójcickiego na zamku w Niepołomicach). Główne wykłady wygłosiło 28 prelegentów. Były po polsku, gdyż zaproszonymi gośćmi byli Polacy - niekoniecznie w sensie obywatelstwa, ale przyznający się do polskości. O właśnie, tylko trzynastu wykładowców pochodziło z polskich instytucji naukowych, pozostałych piętnastu - z USA (7), Francji (4), Anglii (2), Niemiec (1) i Kanady (1). Cóż, jest to zjawisko znane i w ligach piłkarskich.

Najlepsi występują na stałe za granicą. Trochę smutno, ale skoro wolność, to wolność. Kilkoro polskich matematyków zrobiło za oceanem karierę nieosiągalną w Polsce. Pieniądze grają tu drugorzędną rolę, ale nie chcę się na podobne tematy rozpisywać. Może tylko dwie uwagi.

W Rosji i przedtem w Związku Radzieckim matematyka była i jest na naprawdę świadomym poziomie… a jakoś nikt nie chce tam emigrować. Z kolei w Niemczech na stanowisko profesorskie na dowolnym uniwersytecie zgłasza się po kilkunastu kandydatów (koledzy z uniwersytetu w Konstancji mówili, że pewnego roku mieli 120 zgłoszeń, z czego 50 bardzo dobrych, a 20 znakomitych).

Niewiele wykładów z jubileuszowego zjazdu nadaje się do streszczenia w naszym miesięczniku. Przeciętnemu Czytelnikowi nie powiedzą nic tytuły takie, jak "Granice grafów rzadkich i ich zastosowania" czy "Struktura liniowa i geometria podprzestrzeni i przestrzeni ilorazowych dla przestrzeni unormowanych dużego wymiaru". Ten drugi temat prezentowała moja koleżanka z pierwszych lat studiów, Nicole Tomczak.

Za osiągnięcie przedstawione na tym wykładzie była kilkanaście lat temu nominowana do Medalu Fieldsa - równoważnika Nagrody Nobla dla matematyków. Do tej pory tylko jedna kobieta zdobyła to wyróżnienie. Warto też zauważyć wykład Anny Marciniak-Czochry (Uniwersytet w Heidelbergu) "Rola mechanistycznych modeli matematycznych w medycynie na przykładzie modelowania białaczek".

Matematyka wkroczyła do medycyny. Na Uniwersytecie Warszawskim świetne wyniki dotyczące zastosowań matematyki w biologii osiąga grupa pod kierunkiem prof. Jerzego Tiuryna.

Niezrozumiały będzie dla Czytelników tytuł wykładu Wiesławy Nizioł (z prestiżowej École Normale Supérieure) "p-adyczna teoria Hodge’a". A jednak ten właśnie wykład wybrałem do omówienia tutaj.

Geometria światów p-adycznych

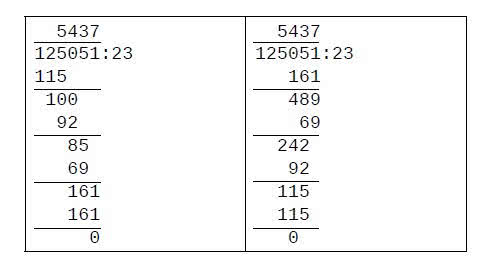
Sprawa zaczyna się prostymi ciekawostkami i łamigłówkami matematycznymi. Czy pamiętasz, Czytelniku, sposób pisemnego dzielenia? Na pewno. Przypomnij sobie beztroskie lata szkoły podstawowej. Podzielmy 125051 przez 23 (to działanie po lewej). Czy wiesz jednak, że można inaczej (działanie po prawej)?

Ten nowy sposób jest ciekawy. Idziemy od końca. Mamy podzielić 125051 przez 23. Przez co trzeba pomnożyć 23, żeby ostatnią cyfrą była 1? Szukamy w pamięci i mamy: d=7. Ostatnią cyfrą wyniku jest 7. Mnożymy, odejmujemy, dostajemy 489. Przez co trzeba pomnożyć 23, żeby na końcu było 9? Oczywiście przez 3. Posuwamy się tak aż do wyznaczenia wszystkich cyfr wyniku. Wydaje nam się to niepraktyczne i trudniejsze niż nasz zwykły sposób - ale to kwestia wprawy!

Sprawa nabiera inny obrót, gdy dzielna nie dzieli się bez reszty przez dzielnik. Wykonajmy dzielenie i zobaczmy, co będzie.

Po lewej sposób zwyczajny, szkolny. Po prawej "nasz dziwny".

Obydwa wyniki możemy sprawdzić przez mnożenie. Pierwszy rozumiemy: jedna trzecia liczby 4675 to tysiąc pięćset pięćdziesiąt osiem i trójka w okresie. Drugi nie ma sensu: co to za liczba, która ma nieskończoną liczbę szóstek z przodu, a potem 8225?

Zostawmy na chwilę pytanie o sens. Pobawmy się. Podzielmy 1 przez 3 a potem 1 przez 7, czyli obliczmy jedną trzecią i jedną siódmą. Otrzymamy łatwo:

1:3=…6666667, 1/7=…(285714)3.

Ten ostatni napis znaczy: z przodu nieskończenie wiele razy powtarza się blok 285714, a na końcu jest trójka. Kto nie wierzy, oto sprawdzenie:

Dodajmy teraz ułamki:

Dodajmy następnie otrzymane dziwne liczby, a otrzymamy (proszę sprawdzić) równie dziwną

……95238095238095238095238010.

Możemy sprawdzić, że jest to równe

Sensu jeszcze nie widać, ale arytmetyka się zgadza.

Jeszcze jeden przykład.

Zwykła, choć duża, liczba 40081787109376 ma ciekawą własność: jej kwadrat też kończy się na 40081787109376. Kto nie wierzy, niech sprawdzi i… poszuka następnej cyfry z lewej strony, tzn. takiej liczby x40081787109376, że (x40081787109376)² kończy się też na x40081787109376.

Wskazówka. Mamy 40081787109376²=16065496 57881340081787109376, zatem następną cyfrą jest dopełnienie trójki do dziesiątki, czyli 7. Sprawdźmy: 740081787109376²=5477210516110077400817 87109376.

Odpowiedź na pytanie dlaczego tak jest - to już trudne zadanie. Łatwiejsze jest: znaleźć podobne końcówki złożone z liczb kończących się na 5. Przedłużając proces znajdowania kolejnych cyfr w nieskończoność, dojdziemy do "liczb" x, y takich, że x²=x, y²=y (no i żadna tych liczb nie jest zerem ani jedynką).

Liczby dziesiętne rozumiemy dobrze. Im dalej po przecinku, tym mniejsze znaczenie ma stojąca tam cyfra. W obliczeniach inżynierskich pierwsza cyfra po przecinku ma znaczenie, druga też, ale w wielu sytuacjach możemy przyjąć, że stosunek obwodu koła do średnicy tego koła jest równy 3,14. Na pewno więcej cyfr liczby pi trzeba uwzględnić w przemyśle lotniczym, ale nie sądzę, by aż dziesięć.

W tytule artykułu pojawiło się nazwisko Stanisława Lema (1921-2006), a także naszej najnowszej noblistki. Panią Olgę Tokarczuk wspomniałem tylko dlatego, że krzyczącą niesprawiedliwością jest, iż literackiej nagrody Nobla nie dostał właśnie Stanisław Lem. Ale o tym nie w naszym kąciku.

Lem często antycypował przyszłość. Zastanawiał się, co będzie, gdy komputery uniezależnią się od ludzi. Ile było ostatnio filmów na ten temat! Lem przewidział i opisał dość dokładnie Internet, czytnik optyczny i farmakologię przyszłości.

Znał matematykę, choć niekiedy traktował ją jako ozdobnik, nie troszcząc się o poprawność rachunków. Na przykład w opowiadaniu "Test" pilot Pirx wchodzi na orbitę B68 z okresem obrotu 4 godziny 29 minut, a instrukcja przewiduje 4 godziny 26 minut. Przypomina sobie, że orbity obliczone są z błędem 0,3 procent. Podaje dane Kalkulatorowi, a ten odpowiada, że wszystko w porządku… Otóż nie. Trzy dziesiąte procenta z 266 minut to niecała minuta. Ale czy ten błąd coś zmienia? Może był celowy?

Dlaczego o tym piszę? Wielu matematyków podnosiło i taką kwestię: wyobraźmy sobie społeczność wyemancypowanych komputerów. Nie mają one naszego ludzkiego wyczucia. Dla nas 1609,12134 oraz 1609,23245 to bardzo bliskie liczby - dobre przybliżenia mili angielskiej. Komputery mogą jednak uznać, że to np. liczby 468146123456123456 i 9999999123456123456 są bliskie. Mają bowiem te same dwunastocyfrowe końcówki.

Im więcej wspólnych cyfr na końcu, tym bliższe są liczby. I to prowadzi do tzw. odległości p-adycznej. Niech p będzie przez chwilę równe 10; dlaczego tylko "przez chwilę", wytłumaczę… za chwilę. Odległością 10-adyczną wyżej napisanych liczb jest 

czyli jedna milionowa - dlatego, że liczby te mają sześć wspólnych cyfr na końcu. Wszystkie liczby całkowite są odległe od zera o jeden lub mniej. Nie będę nawet pisać wzoru, bo to nieistotne. Im więcej identycznych cyfr na końcu, tym bliższe są liczby (dla człowieka odwrotnie, liczą się początkowe cyfry). Ważne jest, że p ma być liczbą pierwszą.

Następnie - komputery lubią zera i jedynki, a więc wszystko widzą w takich wzorkach: 0100110001 1010101101010101011001010101010101111.

W powieści "Głos Pana" Stanisław Lem daje zatrudnienie uczonym, którzy próbują odczytać przysłaną z zaświatów wiadomość, oczywiście kodem zero-jedynkowym. Czy ktoś do nas coś pisze? Lem twierdzi, że "każdy komunikat można odczytać pod warunkiem, że jest to właśnie komunikat, że ktoś chciał nam coś powiedzieć". Ale czy tak jest? Zostawię Czytelników z tą rozterką.

Żyjemy w trójwymiarowej przestrzeni R³. Litera R przypomina, że na osiach x, y, z rozsiadły się liczby rzeczywiste, a więc całkowite, ujemne i dodatnie, zero, wymierne (czyli ułamki) i niewymierne, z którymi Czytelnicy stykali się w szkole (pierwiastki kwadratowe) oraz liczby zwane przestępnymi, niedostępne algebrze (jest nią i liczba π, od ponad dwóch tysięcy lat wiążąca średnicę koła z jego obwodem).

A gdyby na osiach naszej przestrzeni były liczby p-adyczne?

Jerzy Mioduszewski, matematyk z Uniwersytetu Śląskiego, twierdzi, że mogło by tak być, a nawet: że może tak jest. Możemy (twierdzi Jerzy Mioduszewski) z takimi istotami zajmować to samo miejsce w przestrzeni, nie przeszkadzając sobie i nie widząc się nawzajem.

Mamy zatem do zbadania całą geometrię "ich" świata. Jest mało prawdopodobne, że "oni" tak samo myślą o nas i też badają naszą geometrię, a to dlatego, że nasza jest granicznym przypadkiem wszystkich "ich" światów. "Ich" to znaczy wszystkich światów p-adycznych, gdzie p są liczbami pierwszymi. W szczególności p=2 i ten fascynujący świat zero-jedynkowy…

Tu Czytelnik artykułu może wpaść w złość, a nawet w furię. "To takimi głupstwami zajmują się matematycy?" Fantazjują sobie jak przy wódce po kolacji i to za moje pieniądze (=podatnika). A rozpędzić ich na cztery wiatry, niech idą do PGR-u… ach, nie ma już PGR-ów!

Spokojnie. Matematycy zawsze mieli tendencję do takich żartów. Wspomnę tylko twierdzenie o kanapkach: jeżeli mam kanapkę z serem i szynką, to mogę jednym cięciem przeciąć ją tak, by przepołowić bułkę, szynkę i ser. Przydatność takiego czegoś w praktyce jest zerowa. Rzecz w tym, że jest to tylko żartobliwe zastosowanie ciekawego ogólnego twierdzenia z analizy funkcjonalnej.

Na czym polega powaga w zajmowaniu się liczbami p-adycznymi i geometrią z nimi związaną? Przypomnę Czytelnikowi, że liczby wymierne (w uproszczeniu: ułamki) leżą gęsto na linii prostej, a jednak nie wypełniają jej szczelnie.

W "dziurach" mieszkają liczby niewymierne. Jest ich dużo, nieskończenie wiele, ale można też powiedzieć, że ich nieskończoność jest większa niż ta najprostsza, w której liczymy: jeden, dwa, trzy, cztery… i tak do ∞. To jest nasze, ludzkie, wypełnienie "dziur". Taką konstrukcję myślową odziedziczyliśmy po Pitagorejczykach. 

Ale dla matematyka ciekawe i ważne jest to, że nie można inaczej "wypełnić" tych dziur, jak tylko liczbami niewymiernymi i p-adycznymi (dla wszystkich liczb pierwszych p). Dla tych Czytelników, którzy to zrozumieją (a trzydzieści lat temu uczono o tym w każdym liceum), powiem, że chodzi o to, żeby każdy ciąg spełniający warunek Cauchy’ego, był zbieżny.

Przestrzeń, w której jest to prawdą, nazywa się zupełną ("nic w niej nie brakuje"). Przywołam liczbę 547721051611007740081787109376.

Ciąg 0,5 , 0,54 , 0,547 , 0,5477 , 0,54772 i tak dalej jest zbieżny do pewnej granicy, równej w przybliżeniu właśnie 0,5477210516110077400 81787109376.

Natomiast w sensie odległości 10-adycznej ciąg liczb 6, 76, 376, 9376, 109376, 7109376 i tak dalej jest także zbieżny, do "dziwnej" liczby …547721051 611007740081787109376.

Ale i to może być niewystarczającym argumentem, by dawać uczonym pieniądze publiczne. Na ogół bronimy się (my, matematycy), mówiąc, że nie sposób przewidzieć, do czego przydadzą się nasze badania. Jest prawie pewne, że każde się do czegoś przydadzą i że tylko działanie na szerokim froncie ma szanse na sukces.

Jeden z najwspanialszych wynalazków - aparat rentgenowski - został zbudowany po przypadkowym odkryciu promieniotwórczości przez Becquerela. Gdyby nie ten przypadek, prawdopodobnie nic by nie dały wieloletnie badania. "Szukamy sposobu prześwietlenia ciała ludzkiego".

Wreszcie sprawa najważniejsza. Każdy zgodzi się, że rolą matematyka jest umiejętność rozwiązywania równań. I tu nasze dziwne liczby bronią się dobrze. Stosowne twierdzenie (Minkowskiego-Hasse) mówi, że pewne równania mogą być rozwiązane w liczbach wymiernych wtedy i tylko wtedy, gdy mają pierwiastki rzeczywiste i pierwiastki w każdym ciele p-adycznym.

Mniej więcej takie podejście prezentował Andrew Wiles, który rozwiązał najsłynniejsze równanie matematyczne ostatnich trzystu lat - polecam Czytelnikom wpisać do wyszukiwarki "Wielkie twierdzenie Fermata".